
- •§1. Аксіоматична будова теорії натуральних чисел, аксіоми Пеано
- •§2. Метод математичної індукції, його застосування
- •§3. Поняття про алгебраїчні операції та алгебраїчні структури. Група, кільце, поле.
- •§ 4. Поняття комплексного числа
- •§ 5. Форми комплексного числа. Формула Ейлера. Алгебраїчна форма комплексного числа.
- •§6. Дії з комплексими числами, формула Муавра. Корінь з комплексного числа
- •§ 7. Матриці та визначники
- •§ 8. Системи лінійних алгебраїчних рівнянь. Ранг матриці, його обчислення. Критерій Кронекера- Капеллі
- •§9. Системи лінійних рівнянь. Невизначені системи. Метод Гаусса.
- •§ 10. Метод Крамера .
- •§11. Матричний метод розв’язування системи лінійних рівнянь
- •§1. Вектори. Дії з векторами. Колінеарні, компланарні вектори.
- •§ 2. Лінійно-залежні і незалежні системи векторів. Векторний базис.
- •§3. Векторний добуток векторів. Властивості, геометричний зміст
- •§4. Мішаний добуток векторів. Властивості, геометричний зміст
- •§ 5 Рівняння прямої на площині
- •§6. Основні задачі на пряму на площині.
- •§7. Рівняння площини в просторі
- •§8. Основні задачі на площину
- •§9. Рівняння прямої у просторі: перетином двох площин, через дві точки, канонічне
- •§10. Кут між прямою та площиною.
- •§11. Еліпс та його властивості. Канонічне рівняння еліпса.
- •§12. Гіпербола та її властивості. Канонічне рівняння гіперболи
- •§ 13. Парабола та її властивості. Канонічне рівняння параболи.
- •§14. Поверхні другого порядку. Класифікація
Анотація
Підручник призначений для проведення спецкурсу «Вища математика» у 10 класі математичного профілю.
Підручник відповідає програмі спецкурсу «Вища математика»
Морозова О. В.
Матеріал, викладений у підручнику, допоможе вчителю та учням здійснювати підготовку до занять.
Підручник містить підібраний теоретичний матеріал та зразки розв’язування типових задач, що дасть можливість ознайомити учнів з певними теоретичними положеннями з вищої математики та виробити вміння, навички розв’язування деяких типів задач, що сприяють більш глибокому розумінню шкільного курсу математики та дозволяють розв’язати ряд задач прикладного спрямування.
Зміст
Розділ I: «Елементи лінійної алгебри»
Аксіоматична будова теорії натуральних чисел, аксіоми Пеано ……...3
Метод математичної індукції, його застосування……………………….4
Поняття про алгебраїчні операції та алгебраїчні структури. Група, кільце,поле………………………………………………………………8
Поняття комплексного числа……………………………………………11
Форми комплексного числа. Формула Ейлера. Алгебраїчна форма комплексного числа………………………………………………………13
Дії з комплексними числами. Формула Муавра. Корінь з комплексного числа……………………………………………………………………….16
Матриці та визначники…………………………………………………...19
Системи лінійних алгебраїчних рівнянь. Ранг матриці, його обчислення. Критерій Кронекера-Капеллі………………………………26
Системи лінійних рівнянь. Невизначені системи. Метод Гаусса……...30
Метод Крамера…………………………………………………………..34
Матричний метод розв’язування систем лінійних рівнянь……………36
Розділ II: «Елементи аналітичної геометрії»
1. Вектори. Дії з векторами. Колінеарні, компланарні вектори…………40
2. Лінійно-залежні і незалежні системи векторів. Векторний базис……47
3. Векторний добуток векторів. Властивості, геометричний зміст……..52
4. Мішаний добуток векторів. Властивості, геометричний зміст……….55
5. Рівняння прямої на площині…………………………………………….58
6. Основні задачі на пряму на площині…………………………………...62
7. Рівняння площини в просторі…………………………………………...68
8. Основні задачі на площину……………………………………………...72
9. Рівняння прямої у просторі: перетином двох площин, через дві точки, канонічне…………………………………………………………………….75
10. Кут між прямою та площиною……………………………..…………..78
11. Еліпс та його властивості. Канонічне рівняння еліпса……………….81
12. Гіпербола та іі властивості. Канонічне рівняння гіперболи………....84
13. Парабола та її властивості. Канонічне рівняння параболи…………...87
14. Поверхні другого порядку. Класифікація……………………………...89
Використана література…………………………………………………………101
Розділ 1: «Елементи лінійної алгебри»
§1. Аксіоматична будова теорії натуральних чисел, аксіоми Пеано
Вивчаючи курс геометрії, ви звернули увагу на те як вона була побудована. Було введено поняття трьох основних геометричних фігур: точка, пряма, і площина. Ці фігури не мають означень. Потім між ними були введені основні співвідношення: належність точки прямій, прямої площині, тощо. Були сформульовані очевидні твердження, які неможливо було ні спростувати, ні довести. Їх називали аксіомами. Далі, використовуючи аксіоми, доводили інші твердження, які називали теоремами, і виражали властивості фігур. При побудові геометрії точки, прямі і площини були об’єктами, природа яких для побудови формальної геометрії байдужа.
За такою схемою можна побудувати інші аксіоматичні теорії.
Розглянемо аксіоматичну побудову теорії натуральних чисел (аксіоми Пеано).
Аксіоми Пеано – одна із систем аксіом для натуральних чисел.
В 1860-х роках Герман Грасеман показав, що багато тверджень арифметики можуть виводитись через властивості наступного числа та математичну індукцію. Використовуючи його роботи, Ріхард Дедекінд в 1888 р. запропонував систему аксіом для натуральних чисел, яка в 1889 р. була уточнена італійським математиком Джузеппе Пеано.
Аксіоми Пеано дозволили формалізувати арифметику.
Означення.
Натуральними числами називають елементи
будь-якої непорожньої множини М , в якій
для елементів а, b
існує відношення «b
йде
за а»( число «йде за а» позначають
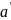 )
, що задовольняє такі аксіоми.
)
, що задовольняє такі аксіоми.
Існує число 1, яке не йде ні за яким числом, тобто ≠
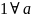 .
.Для будь-якого а існує наступне за ним число , і при тому єдине, тобто а=b
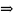 =
=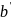 .
.Будь-яке число йде не більше, ніж за одним числом, тобто = ⇒ а=b.
Аксіома індукції. Будь-яка множина М натуральних чисел, що має властивості:
а) 1 є М; б) а є М ⇒ (а+1) є М , містить усі натуральні числа, тобто збігається з N.
У запису аксіом знак «= » означає, що елементи множини збігаються, а знак «≠» - різні елементи множини.
Аксіома індукції відіграє важливу роль у математиці, вона й дає можливість довести теорему про законність індуктивних доведень.
Теорема.
Якщо деяка теорема, формулювання якої
містить натуральне число n,
доведена для випадку, коли n=1,
і за припущенням, що вона правильна для
n,
доведена для натурального числа
 ,
то ця теорема справджується для будь-якого
n.
,
то ця теорема справджується для будь-якого
n.
Цю теорему покладено в основу принципу математичної індукції.
§2. Метод математичної індукції, його застосування
Вивчаючи навколишній світ, нам часто доводиться на підставі результатів спостережень і дослідів робити висновки.
Загальні висновки, отримані на підставі окремих випадків, називають індуктивними, а сам метод таких міркувань – індуктивним методом або індукцією (від лат. іnductio - наведення).
Наприклад, задовго до відкриття законів руху Землі люди зробили висновок, що Сонце вранці встає на сході, а ввечері зникає за обрієм на заході. Цей висновок є індуктивним: адже він базувався лише на спостереженнях.
Звісно за допомогою індукції не завжди можна отримати правильні висновки. Так, якщо у вашій і у сусідній школах серед вчителів математики немає чоловіків, то це не означає, що всі вчителі математики – жінки.
Незважаючи на необхідність ставитися до індуктивних висновків з певним ступенем недовіри, індуктивний метод знаходить широке застосування в математиці.
При розв’язуванні математичних задач інколи виникає потреба довести, що деяке твердження (рівність або нерівність) правильне при будь-якому натуральному значенні n або починаючи з деякого значення n. Для розв’язування таких задач застосовують принцип математичної індукції.
Доведення тверджень цим методом можна провести в три етапи:
1) перевірка твердження при n=1 або при найменшому допустимому значенні n. На цьому етапі у дане твердження слід підставити найменше допустиме значення n і переконатися, що твердження правильне.
2) припущення індукції.
На цьому етапі слід припустити, що твердження правильне при n=k . У дане твердження замість n потрібно підставити k і вважати, що це твердження істинне.
3)доведення індукції.
На цьому етапі потрібно, використовуючи припущення індукції, довести, що твердження правильне при n=k+1. Якщо це вдалося зробити, то твердження вважають доведеним.
Наведемо приклади використання принципу математичної індукції.
Приклад 1.
Довести,
що
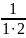 +
+
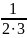 +…+
+…+
 =
=
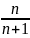 правильна
при будь-якому натуральному n.
правильна
при будь-якому натуральному n.
Розв’язання.
Перевіримо, чи правильне дане твердження при n=1.
=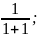
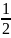 =
. Твердження правильне.
=
. Твердження правильне.
Припустимо, що твердження правильне при n=k, тобто правильною є рівність
+
+ … +
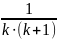 =
=
 .
.
Використовуючи припущення індукції доведемо, що твердження правильне при n=k+1, тобто потрібно довести, що виконується рівність
+
+ … +
+
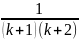 =
=
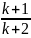 ;
;
+
+ … +
+
=
+
=
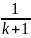 ( k+
( k+
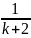 )
=
)
=
=
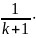
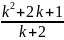 =
=
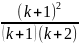 =
,
=
,
що й треба було довести.
Приклад 2.
Довести, що правильна рівність
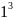 +
+
 +
+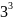 + … +
+ … +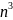 =
=
 ,
де
n
є
N.
,
де
n
є
N.
Розв’язання
Перевіримо правильність твердження при n = 1.
=
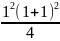 ;
;
1
=
 ;
;
1=1.
Твердження правильне.
Припустимо, що твердження правильне при n=k, тобто виконується рівність:
+
+
+ … +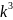 =
=
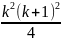 .
.
Використовуючи припущення індукції, доведемо, що рівність правильна при n=k+1. Тобто потрібно довести, що правильна рівність
+
+
+ … +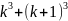 =
=
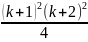 .
.
+
+
+ … +
+
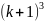 =
+
=
=
+
=
=
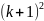 (
( )
=
)
=
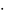
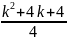 =
,
=
,
що й треба було довести.
Приклад 3.
Довести,
що
 7n
7n
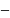 5 ,
якщо
n
Є N.
5 ,
якщо
n
Є N.
Розв’язання
Перевіримо правильність твердження при n = 1.
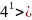 7
7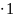 5 ;
5 ;
4 7-5;
7-5;
4 2.
Твердження правильне.
Припустимо,
що твердження правильне при n = k, тобто
виконується нерівність
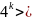 7k-
5.
7k-
5.
Використовуючи
припущення індукції доведемо, що
твердження правильне при
n
= k
+
1,
тобто потрібно довести , що
 7(k+1)
-5 = 7k
+ 2;
7(k+1)
-5 = 7k
+ 2;
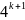 =
=
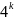 4
4
(7k-
5) =28k
– 20.
4
4
(7k-
5) =28k
– 20.
Розглянемо різницю чисел 28k - 20 і 7k -2.
28k – 20- (7k +2) =28k – 20- 7k -2 = 21k-22.
Враховуючи, що k – натуральне число не менше 2, зазначимо, що знайдена різниця додатня, а отже
28k – 20 7k +2, тому 28k – 20 7k +2.
7k +2, що й треба було довести.
Приклад 4.
Доведіть,
що
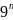 -8n-1
ділиться
на 16 при будь-якому натуральному n.
-8n-1
ділиться
на 16 при будь-якому натуральному n.
Розв’язання
Перевіримо, чи правильне твердження при n=1.
Одержимо
 - 8
1-1
=9 -8 -1 = 0
- 8
1-1
=9 -8 -1 = 0
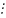 16 .
16 .
Отже, твердження правильне.
Припустимо, що твердження правильне при n=k, тобто
(
 – 8k
-1)
16 .
– 8k
-1)
16 .
Використовуючи припущення індукції доведемо, що твердження правильне при n = k + 1.
Тобто
(
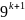 – 8(k
+1) -1)
16,
– 8(k
+1) -1)
16,
– 8(k +1) -1 = 9 - 8 k -8 -1 =
= 9 - 9 8k – 9 + 64k= 9 ( -8k-1) +64 k.
Перший доданок кратний 16, бо -8k-1) 16 за припущенням індукції.
Другий доданок кратний 16, бо 64 = 16 4, а отже і сума буде кратною 16.
Тобто ( – 8(k +1) -1) 16, що й треба було довести.
Задачі для самостійного розв’язування.
Доведіть, що при будь-якому натуральному n виконується рівність:
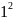 +
+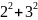 +…
+
+…
+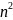 =
=
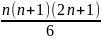 ;
;+
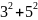 +…
+
+…
+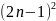 =
=
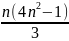 ;
;+
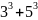 +…
+
+…
+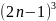 =
=
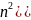 -1);
-1);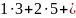 3
7
+ … + n (2n+1) =
3
7
+ … + n (2n+1) =
 ;
;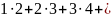 …
+
n (n+1)=
…
+
n (n+1)=
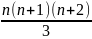 ;
;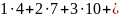 …
+
n (3n+1)=
…
+
n (3n+1)=
 ;
;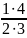 +
+
 +
+
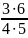 + … +
+ … +
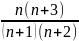 = +
= +
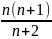 ;
;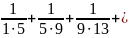 …
+
…
+
 =
=
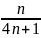 ;
;(1-
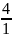 )(1-
)(1-
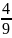 ) (1-
) (1-
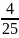 )
…
(1-
)
…
(1-
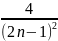 =
=
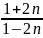 .
.
Доведіть, що для будь-якого натурального n.
(
 ;
;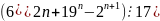 ;
;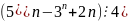 ;
;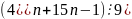 ;
;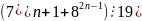 ;
;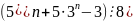 ;
;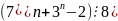 ;
; ;
; -
5
-
5
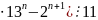 ;
; .
.
Доведення нерівностей.
доведіть нерівність
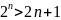 ,
де
n
Є
N
,
n
,
де
n
Є
N
,
n
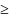 3 ;
3 ;доведіть нерівність
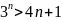 ,
де
n
Є
N
,
n
3;
,
де
n
Є
N
,
n
3;доведіть нерівність
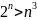 ,
де n
Є N
, якщо n
10.
,
де n
Є N
, якщо n
10.
