15. Коммутационные схемы

Возможность применения математической логики к техническим вопросам была обнаружена в 30-х годах ХХ века. Была замечена, например, связь между электрическими цепями и логическими функциями. Это открытие дало толчок к развитию ЭВМ.

Основным элементом релейно-контактных устройств является электромеханическое реле (переключатель). Реле может размыкать и замыкать цепь. Присвоим р значение 1, когда цепь замкнута (ток проходит), и значение 0, когда цепь разомкнута (ток не проходит).

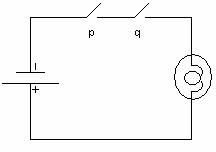
Рассмотрим электрическую цепь на рис. 1. При таком расположении контактов p и q лампочка будет гореть (т.е. схема имеет значение 1), если оба переключателя p и q замкнуты (т.е. имеют значения 1). Таким образом, эта схема соответствует логической формуле p q, а такое расположение переключателей называется логическим элементом «p и q» или схемой логического умножения, его обозначают на схеме как на рис. 2.

Рассмотрим теперь схему на рис. 3. В этой цепи лампочка будет гореть и значение схемы равно 1, если хотя бы один из двух контактов p или q, или оба, будут замкнуты, т.е. или p=1, или q=1, или оба p=q=1. Таким образом, эта схема соответствует логической формуле p q, а такое расположение переключателей называется логическим элементом «p или q» или схемой логического сложения. Изображают на схемах как на рис. 4. Если имеем схему с одним переключателем p, который обладает свойством, что лампочка загорается тогда и только тогда, когда p разомкнут (т.е. схема имеет значение 1, когда р=0, и значение 0, когда р=1), то эта схема соответствует . Такой логический элемент называется «не р» или инвертором, его часто изображают на схемах как на рис. 5.

16. Двойственность. Булева алгебра и теория множеств.

Функция f*(x₁,..,x_n), называется двойственной к функции f(x₁,..,x_n), если . Функция двойственная сама себе, называется самодвойственной. Отношение двойственности симметрично f*=g,  g*=f

Двойственную функцию можно получить с помощью таблицы истинности, если заменить все значения на противоположные

Пример: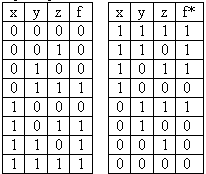 f=f*

Принцип двойственности: если в формуле F, представляющей функцию f, все знаки функций заменить на знаки двойственных функций, то полученная формула F* будет представлять функцию f*, двойственную функции f. В булевой алгебре принцип двойственности имеет более конкретный вид, вытекающий из выше приведенного примера: если в формуле F, представляющей функцию f, все конъюнкции заменить на дизъюнкции, дизъюнкции - на конъюнкции, 1 на 0, 0 на 1, то получим формулу F*, представляющую двойственную функцию f*. Таким образом, ДНФ соответствует КНФ, КНФ – ДНФ, СДНФ – СКНФ, СКНФ – СДНФ. Справедливо утверждение: если f₁=f₂, то f*₁=f*₂

Булева алгебра и теория множеств

Определение. Всякая алгебра, содержащая две бинарные и одну унарную операции, которые удовлетворяют соотношениям 1 - 9 (1 Коммутативность, 2 Ассоциативность, 3 Дистрибутивность, 4 Идемпотентность, 5 Закон поглощения, 6 Закон де Моргана, 7 Закон двойного отрицания, 8 Свойства констант, 9 Закон противоречия) называется булевой.

Таким образом, булевыми алгебрами будут:

а) - булева алгебра всех логических функций с операциями конъюнкции, дизъюнкции, отрицания;