29. Раскраска графов. Планарность.

Пусть н-граф без петель. Раскраской графа называется такое приписание цветов (или натуральных чисел) его вершинам, что никакие две смежные вершины не получают одинакового цвета (т.е. если ребро, то вершины и имеют разные цвета). Хроматическим числом графа называется минимальное число цветов, требующееся для раскраски .

Многие практические задачи сводятся к построению раскраски графов: задачи составления расписаний, распределения оборудования, проектирования некотоых технических изделий, раскрашивания географических карт и т.д.

Для некоторых известных графов хроматическое число легко найти, например, , , , , где - полный граф с вершинами, - его дополнение, - двудольный граф, - дерево. В общем случае нет формулы, по которой можно было бы вычислить хроматическое число графа. Известны только некоторые оценки этого числа. Наиболее простая оценка имеет вид: , где - максимальная степень вершин графа .

Поскольку формула для определения хроматического числа неизвестна, то задача нахождения минимальной раскраски труднорешаема. Рассмотрим простой алгоритм построения раскраски графа, который в общем случае не приводит к минимальной раскраске, но приводит к раскраскам, близким к минимальным.

Алгоритм последовательной раскраски.

1. Произвольной вершине графа присваиваем цвет 1.

2. Если вершины 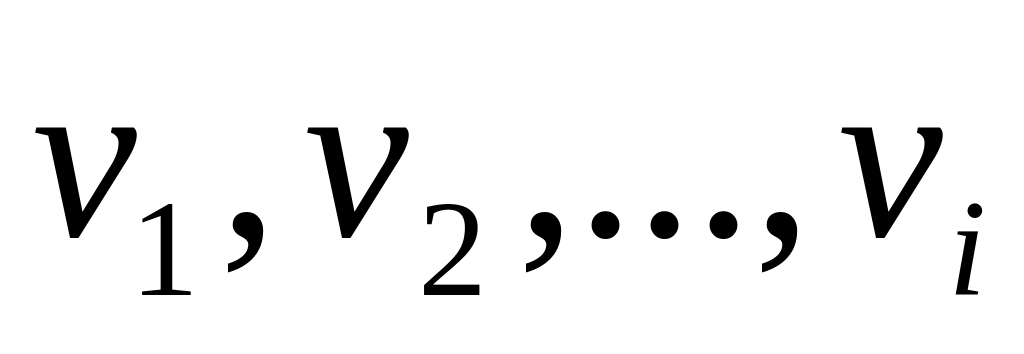раскрашены 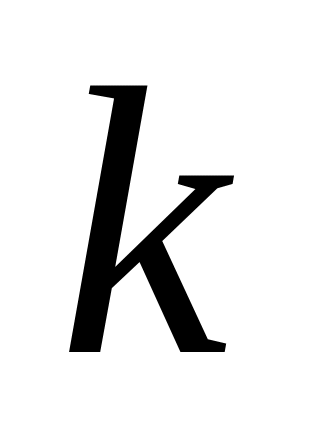цветами 1,2,…, (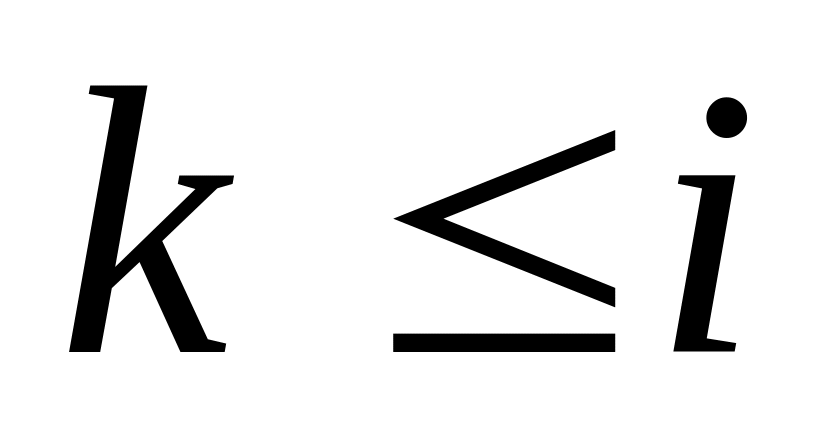 ), то

новой произвольно взятой вершине припишем минимальный цвет, не использованный при раскраске вершин из её окружения, т.е. множества вершин таких, что . Обозначим через окружение вершины .

Теорема Понтрягина-Куратовского. Граф планарен тогда и только тогда, когда он не содержит подграфа, гомеоморфного и .

Другая эквивалентная формулировка критерия планарности: граф планарен тогда и только тогда, когда он не содержит подграфов, стягиваемых (т.е. получаемых последовательностью отождествлений вершин, связанных рёбрами) к графу или .

На практике требуется ответить на вопросы: а)будет ли граф планарным?; б) если будет, то как уложить его на плоскости? На первый вопрос отвечает теорема Понтрягина-Куратовского, хотя практически применить её не всегда просто.

Если граф не планарен, то, удалив некоторые его рёбра (т.е. перенося их на другую плоскость), можно получить планарный граф. Минимальное число рёбер, которое необходимо удалить из графа для получения его плоского изображения, называется числом планарности графа (иногда обозначают ). Если после вынесения этих рёбер на вторую плоскость, на ней вновь получают непланарный граф, то удаляют отдельные рёбра на следующую плоскость и т.д. Минимальное число плоскостей , при котором граф разбивается на плоские части называется толщиной графа (толщину иногда обозначают ).