ЗАТВЕРДЖЕНО

Наказ Міністерства освіти і науки,

молоді та спорту України

29 березня 2012 року № 384

Форма № Н-6.01

Міністерство освіти і науки України

ПЕРВОМАЙСЬКИЙ ПОЛІТЕХНІЧНИЙ КОЛЕДЖ

Первомайського політехнічного інституту

Національного університету кораблебудування імені адмірала Макарова

КУРСОВИЙ ПРОЕКТ

з дисципліни «Комп’ютерна схемотехніка»

на тему: Загальна характеристика скінченних автоматів

Студента 3 курсу 311-ОКС групи

напряму підготовки

6.050102 «Комп’ютерна інженерія»

спеціальності 5.05010201 – «Обслуговування комп’ютерних систем і мереж»

Самарасінгхе К.В.

Керівник: викладач відділення «Обслуговування комп’ютерних систем» Бойко Д.А.

Оцінка: _________________

Члени комісії _______________ Бойко Д.А.

_______________ Калашніков О.В.

_______________ Клига Л.Ф.

м. Первомайськ – 2013 рік

ЗМІСТ

ВСТУП	3
1 КЛАСИФІКАЦІЯ СКІНЧЕННИХ АВТОМАТІВ	4
1.1 Акцептори і розпізнавачі	5
1.2 Перетворювачі (Трансдуктори)	11
1.2.1 Автомат Мілі	11
1.2.2 Автомат Мура	13
1.3 Відмінність між детермінованими і недетермінованими автоматами	15
2 ВИКОРИСТАННЯ КІНЦЕВИХ АВТОМАТІВ	18
2.1 Розпізнавання регулярних виразів	18
2.1.1 Мови й регулярні вирази	19
2.1.2 Автоматні граматики й регулярні вирази	21
2.3 Методи захисту інформації	22
ВИСНОВОК	26
ЛІТЕРАТУРА	27

ВСТУП

Дослідження в галузі теорії автоматів почалися ще в середині 50-х років минулого століття. Не дивлячись на свою простоту, модель скінченного автомата виявилася надзвичайно зручною у застосуванні не тільки в інформатиці, але і в багатьох інших галузях інженерної діяльності. Великий інтерес до цієї теорії пояснюється саме широкими можливостями її застосування.

Без перебільшення можна сказати, що теорія автоматів є одним з фундаментальних блоків сучасної теоретичної і практичної інформатики. Разом з класичними додатками теорії автоматів, такими як проектування вбудованих систем логічного управління, обробка текстів і побудова компіляторів штучних мов, останнім часом з'явилися нові, нетрадиційні області застосування цієї теорії - специфікація і верифікація систем взаємодіючих процесів (зокрема, протоколів комунікації), мови опису документів і об'єктно-орієнтованих програмних систем, оптимізація логічних програм та інші.

1 Класифікація скінченних автоматів

Скінченні автомати можуть розв'язувати велику кількість задач, серед яких автоматизація проектування електронних приладів, проектування комунікаційних протоколів, синтаксичний аналіз та інші інженерні застосування. В біології і дослідженнях штучного інтелекту, автомати або їх ієрархії іноді використовуються для описання неврологічних систем і в лінгвістиці для описання граматики природніх мов.

Скінченний автомат - в теорії алгоритмів математична абстракція, що дозволяє описувати шляхи зміни стану об'єкту залежно від його поточного стану і вхідних даних, за умови, що загальна можлива кількість станів кінцева. Скінченний автомат є окремим випадком абстрактного автомата.

Існують різні варіанти завдання скінченного автомата. Наприклад, скінченний автомат може бути заданий за допомогою п'яти параметрів:

,

де Q – кінцева множина станів автомата;

q0 – початковий стан автомата ( );

F – множина кінцевих (або допустимих) станів, таких що ;

Σ – допустимий вхідний алфавіт (кінцева множина допустимих вхідних символів), з якого формуються рядки, що прочитуються автоматом;

δ – задане відображення множини в множину підмножини Q:

(іноді δ називають функцією переходів автомата).

Автомат починає роботу в стані q0, прочитуючи по одному символу вхідного рядка. Лічений символ переводить автомат в новий стан із Q відповідно до функції переходів. Якщо після закінчення прочитування вхідного слова (ланцюжки символів) автомат опиняється в одному з допускаючих станів, то слово «приймається» автоматом. В цьому випадку говорять, що воно належить мові даного автомата. Інакше слово «відкидається».

Кінцеві автомати широко використовуються на практиці, наприклад в синтаксичних, лексичних аналізаторах, і тестуванні програмного забезпечення на основі моделей.

1.1 Акцептори і розпізнавачі

Акцептори і розпізнавачі (також виявлювачі послідовностей) продукують двійковий вихід, кажучи або так або ні на питання прийняті автоматом вхідні дані чи ні. Всі стани СА можуть бути або допустимі або ні. Коли всі вхідні дані оброблені, якщо поточний стан є допустимим, значить вхід прийнятий; інакше відхилений. Як правило на вхід подаються символи (літери); дії не використовуються. Приклад на зображенні показує СА який приймає слово «nice». В цьому СА єдиний допустимий стан це 7.

Рисунок 1. СА акцептор: виконує розбір слова "nice"

Автомат також може бути описаний як такий, що визначає мову, яка містить всі слова розпізнавані цим автоматом, але не ті які ним відхиляються; тоді ми кажемо, що ця мова розпізнається автоматом. За визначенням, мови розпізнавані СА це регулярні мови тобто мова є регулярною якщо існує деякий СА, який розпізнає її

Робота розпізнавача може бути представлена у вигляді послідовності тактів. Щоб описати роботу розпізнавача, уведемо поняття конфігурації. Конфігурація розпізнавача визначається станом s_i і ще не прочитаною частиною вхідного ланцюжка α' на стрічці: (s_i, α').

У кожному такті відбувається зміна конфігурації розпізнавача. Якщо такту роботи відповідає конфігурація (s_k, pα'), де p – символ, розташований під читаючою головкою, і, якщо визначено функцію переходів φ(s_k, p)=s_i, те формується нова конфігурація (s_i, α'), що відповідає наступному такту роботи.

Зміну конфігурацій позначають спеціальним символом і записують так:

(s_k,α) |→ (s_i, α').

Якщо існує послідовність конфігурацій, що відповідає послідовності тактів роботи розпізнавача А

(s_i, α₁₎ |→ (s_i2, α₂₎ |→… |→ (s_ik, α_k),

то позначають її у такий спосіб:

(s_i1, α₁₎ |→^* (s_ik, α_k)

Конфігурація, утворена початковим станом s₀ і ще не прочитаним вхідним ланцюжком α називається початковою конфігурацією й позначається (s₀, α).

Конфігурація, утворена кінцевим станом з множина F і порожнім ланцюжком, називається кінцевою або заключною конфігурацією.

Вхідне слово (ланцюжок) α називається припустимим для розпізнавача А, якщо при послідовному читанні символів α с вхідної стрічки розпізнавач переходить із початкової конфігурації в одну з кінцевих конфігурацій.

Множина ланцюжків L, що допускають распознавателем А, назвемо мовою, що допускають цим распознавателем L(А).

L(А) = {α | α* й (s₀, α) |→ ^* (s_k, F) і s_k F}

Як ілюстрація розглянемо роботу розпізнавача А_1, що визначаться множинами: P = {0, 1}, S = {A, B, C, D}, F = {D}. Функція переходів цього розпізнавача задається таблицею 1:

Таблиця 1. переходів розпізнавача А₁

pk	0	1
A	B	A
D	C	A
C	D	C
D	-	-

Рисунок 2. Діаграма переходів розпізнавача А1

Робота розпізнавача для вхідного ланцюжка 01001 може бути представлена у вигляді послідовності конфігурацій (A, 01001) → (B, 1001) → (A, 001) → (B, 01) → (C, 1) → (C, 0), яка показує, що ланцюжок не допускається розпізнавачем А₁, оскільки він не досягає скінченного стану після прочитання всіх вхідних символів.

Уведені поняття дозволяють визначити зв'язок між формальними граматиками й розпізнавачами шляхом установлення відповідності мов, породжуваних граматиками, і мов, що допускають розпізнавачами.

Для автоматних граматик і розпізнавачей відповідність цих понять визначається наступним твердженням.

Для кожного розпізнавача існує А-граматика, що породжує мову, що збігається з множиначю ланцюжків, що допускає розпізнавач.

Цій діаграмі відповідає лівостороння граматика, схема якої має вигляд:

R = {<I>→<B>b, <B>→<B> b, <B>→<Z> a, <Z>→<Z> a}.

Щоб показати справедливість цього твердження, розглянемо побудову граматики по заданій діаграмі переходів розпізнавача. Така побудова полягає в наступному. Для кожної пари станів розпізнавача X й Y, з'єднаних дугою, що виходить із X, що заходить в Y і позначеної вхідним символом p, побудуємо правило граматики виду <X>> a <Y>, якщо стан Y не є кінцевим станом розпізнавача, або – правило <X>> a, якщо Y – скінченний стан.

Отримана в такий спосіб множина правил визначає граматику, що породжує мову, що допускає заданим розпізнавачем. Дійсно, кожен породжуваний розпізнавачем ланцюжок L буде викликати послідовність переходів розпізнавача, а кожному переходу відповідає правило граматики, тому послідовність переходів при читанні символів ланцюжка L буде відповідати послідовності застосування правил граматики, тобто виводу цього ланцюжка в побудованій граматиці. Застосуємо описаний спосіб побудови до розпізнавача А₁. У результаті одержимо граматику зі схемою:

R= <A> → 1 <A>,<A> → 0 <B>, <B> → 1 <A>, <B> → 0 <C>, <C>→ 1 <C>, <C>→ 0.

Розглянемо ще один приклад побудови граматики для розпізнавача А₂, що заданий діаграмою переходів, зображеної на рис. 3.

Рисунок 3.Діаграма переходів розпізнавача А2

Цей розпізнавач має однокінцевей стан, що збігається з його початковим станом F= {I}.

Цю обставину варто врахувати при побудові правила граматики, що відповідає переходу зі стану B у стан I.

Сама граматика, побудована по діаграмі розпізнавача А₂, має вигляд:

R=<I>→0<I>

<I>→1<A>

<A>→0<A>

<A>→1<B>

<B>→0<B>

<B>→1<I>

Друге твердження, що показує зв'язок автоматних граматик і розпізнавачей, формулюється в такий спосіб.

Для кожної А-граматики, що породжує мову, що не містить порожнього ланцюжка, існує розпізнавач, множина припустимих ланцюжків якого збігається з мовою, породжуваною заданою граматикою.

Щоб показати виправданість цього твердження, спочатку опишемо спосіб побудови розпізнавача по заданій граматиці.

Побудова передбачає виконання двох етапів: спочатку здійснюється перетворення заданої граматики, а потім побудова діаграми переходів розпізнавача.

Перетворення заданої граматики виконується в такий спосіб.

Доповнимо алфавіт V_А ще одним символом <Z>.Всі заключні правила граматики виду <A>→ a перетворимо в правила виду <A>→ a<Z>. Додамо правило <Z>→ $. Інші правила залишимо без зміни.

Побудова діаграми переходів розпізнавача виконується за наступними правилами:

1) поставимо у відповідність кожному нетермінальному символу вузол графа,

2) для кожного правила <A>a<B> з'єднаємо дугою вузли A й B і відзначимо цю дугу символом a,

3) вузол, відзначений початковим символом граматики, приймемо як початковий вузол, а вузли, відзначені символом <Z>, як скінченні вузли графа (вузли, для яких є правила Z > $, уважаємо заключними).

У результаті побудови одержуємо розпізнавач, що допускає мова, породжувана заданою граматикою, оскільки кожному виводу ланцюжка → у заданій граматиці відповідає послідовність переходів у побудованій діаграмі переходів розпізнавача.

Як приклад побудуємо розпізнавач для граматики Г_2.1

Г_2.1: R= {<I>→ a <I>, <I>→ a <A>, <A>→ b <A>, <A>→ b}

Після перетворення одержуємо граматику Г_2.1' і діаграму переходів шуканого розпізнавача у вигляді:

Г_2.1': R= {<I>→ a <I>, <I>→ a <B>, <B>→ b<B>, <B>→ b<Z>, <Z>→ $}

Діаграма розпізнавача A₃, побудована по цій граматиці, зображена на рис.4

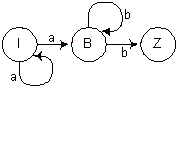
Рисунок 4.Діаграма переходів розпізнавача A3, побудованого для правобічної граматики Г2.1'