
- •Длина пути s пройденного точкой за промежуток времени от t1 до t2 задается интегралом
- •Законы Ньютона.
- •И.С.О. Энергия. Работа. Кинетическая и потенциальная энергия. Закон сохранения энергии. Границы применимости з.С.Э.
- •1.2 Добротностью колебательной системы называется безразмерная величина q, равная произведению 2 на отношение энергий
- •Экспериментальные основы с.Т.О. Постулаты Эйнштейна. Пространство время и системы отсчета в с.Т.О. Преобразование Лоренца и их кинематические следствия.
- •Второй закон термодинамики.
- •1 . Поле бесконечной однороно заряженной плоскости. Рассмотрим поле создаваемое бесконечной плоскостью заряженной положительно с постоянной поверхностной плотностью .
- •2. Магнитное поле в центре кругового тока.
- •Энергия магнитного поля
- •Принцип соответствия Бора: выводы и законы квантовой механики при больших значениях квантовых чисел должны соответствовать выводам и законам классической физики.
- •Фермионы и бозоны.
Энергия магнитного поля
Магнитное поле порождается током и исчезает вместе с ним. Следовательно, часть энергии тока всегда идет на создание магнитного поля.
Магнитное поле обладает энергией, равной работе, затраченной током на его создание.
Пусть в контуре изменяется ток, что сопровождается изменением магнитного потока. dФ=LdI
При изменении потока ток совершает работу dA=IdФ=LIdI
Полная
работа тока по созданию магнитного
потока от 0 до Ф (т.е. нарастания тока от
0 до I) равна![]() .
Следовательно, энергия магнитного поля,
связанного с контуром
.
Следовательно, энергия магнитного поля,
связанного с контуром![]() .
.
В зависимости от величины магнитной проницаемости все магнетики подразделяются на три группы:
1)
диамагнетики, у которых
![]() ,
,
2)
парамагнетики, у которых
![]() ,
,
3)
ферромагнетики, у которых
![]() достигают больших значений.
достигают больших значений.
Вещества, намагничивающиеся во внешнем поле против направления магнитного поля, называются диамагнетиками (Ag, Au, Cu и др.)
Вещества, намагничивающиеся во внешнем магнитном поле по направлению поля (Pt, Al) парамагнетики.
Сильномагнитные вещества – ферромагнетики – вещества, обладающие спонтанной намагниченностью, т.е. они сохраняют намагниченность при отсутствии внешнего магнитного поля. Приведём графики зависимости намагниченности J от H.
З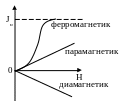
 ависимость
намагниченности J
от напряжённости магнитного поля H,
представляется
петлёй гистерезиса.
ависимость
намагниченности J
от напряжённости магнитного поля H,
представляется
петлёй гистерезиса.
0–1 – ферромагнетик намагничен до насыщения;
1–2 – при Н=0 в ферромагнетике остаётся остаточная намагниченность Iос;
2–3 – уменьшение намагниченности до нуля. Нс – коэрцитивная сила;
3–4 – при увеличении противоположного поля ферромагнетик намагничивается, достигая насыщения в точке 4; 4–5–6 – размагничивание ферромагнетика.
6–1 – новое перемагничивание до насыщения.
Для каждого ферромагнетика имеется определённая температура, называемая точкой Кюри, при которой он теряет свои магнитные свойства. При нагревании выше точки Кюри ферромагнетик превращается в парамагнетик.
Условия
на границе раздела двух магнетиков:
При переходе через границу раздела двух
магнетиков с различными магнитными
проницаемостями μ1
и μ2
силовые линии магнитного поля испытывают
преломление. Для того, чтобы выяснить,
как происходит преломление линий поля
необходимо установить для его нормальных
и тангенциальных составляющих граничные
условия:
![]() ,
,![]() ,
,
![]() ,
,
![]() .Из
граничных условий можно сделать вывод:
Если граница раздела сред ортогональна
линиям маг. индукции, т.е.
.Из
граничных условий можно сделать вывод:
Если граница раздела сред ортогональна
линиям маг. индукции, т.е.![]() ,то
,то
![]() и
вектор маг. индукции не изменяется при
переходе через границу
и
вектор маг. индукции не изменяется при
переходе через границу![]() .
Если граница раздела сред касается
линий маг. индукции, т.е.
.
Если граница раздела сред касается
линий маг. индукции, т.е.
![]() и
и
![]() ,
то
,
то
![]() и напряженность маг. поля не изменяется
при переходе через границу:
и напряженность маг. поля не изменяется
при переходе через границу:
![]() ,
,
![]() .
.
№ 19. Постоянный ток в металлах. Электродвижущая сила. Законы Ома и Джоуля–Ленца. Плотность тока, закон Ома в дифференциальной форме. Правила Кирхгофа и их физический смысл. Мощность тока.
Носителями электрического тока в металле являются электроны проводимости. При образовании кристаллической решётки электроны внешних оболочек атомов (валентные электроны) обобществляются и кристалл представляет собой решётку неподвижных ионов, между которыми хаотически движутся свободные электроны, образуя электронный газ, обладающий свойствами идеального газа.
Согласно
классической теории электропроводности
Друде–Лоренца, электроны обладают
энергией теплового движения той же, что
и молекулы одноатомного газа. Средняя
скорость теплового движения электронов
![]() ,
где k
– постоянная Больцмана, me
– масса электрона. Хаотическое тепловое
движение электронов не может привести
к возникновению тока.
,
где k
– постоянная Больцмана, me
– масса электрона. Хаотическое тепловое
движение электронов не может привести
к возникновению тока.
При помещении металлического проводника во внешнее электрического поле в нём возникает электрический ток. Электроны, участвуя в тепловом хаотическом движении, движутся упорядоченно.
Даже
при предельно допустимых значениях
плотности тока, средняя скорость
![]() упорядоченного движения электронов,
обуславливающий электрический ток,
значительно меньше их скорости теплового
движения
упорядоченного движения электронов,
обуславливающий электрический ток,
значительно меньше их скорости теплового
движения
![]() ,
т.е.
,
т.е.
![]() .
.
Величина,
равная отношению работы, которую
совершают сторонние силы при перемещении
точечного положительного заряда вдоль
всей цепи, включая и источник тока, к
заряду , называется электродвижущей
силой источника тока:![]()
Работа
против сил электрического поля, по
определению равна:![]()
Сторонние силы можно охарактеризовать работой, которую они совершают над перемещающимися по цепи зарядами. Эта работа складываеться из работы, совершаемой против электрического поля внутри источника тока (Аист) и работы, совершаемой против сил сопротивления среды (А’), т.е. Аст=Аист+А’
Если
полюсы источника разомкнуты, то
![]() и тогда
и тогда
![]()
т.е.
эдс источника тока при разомкнутой
внешней цепи равна разности потенциалов,
которая создается на его полюсах. Т. о.,
размерность эдс совпадает с размерностью
потенциала. Поэтому измеряется в тех
же единицах, что и![]() - в вольтах. Стороннюю силу Fст, действующую
на заряд, можно представить в виде
- в вольтах. Стороннюю силу Fст, действующую
на заряд, можно представить в виде
Fст=E*q
Векторную
величину Е* называют напряженностью
поля сторонних сил. Работу сторонних
сил над зарядом q на всём протяжении
замкнутой цепи можно выразить следующим
образом:![]()
Разделив
эту работу на q , получим эдс, действующую
в цепи:![]()
Таким образом, эдс, действующая в замкнутой цепи, может быть определена как циркуляция вектора напряженности поля сторонних сил.
Законы
Ома.
Рассмотрим линейную электрическую
цепь, состоящую из источника постоянного
тока с ЭДС и постоянным внутренним
сопротивлением r,
реостата, ключа К и соединительных
проводов. Пусть электрические потенциалы
в точках участка цепи АВ равны
![]() и
и
![]() ,Тогда
по определению напряжения U
на участке АВ равно
,Тогда
по определению напряжения U
на участке АВ равно
![]() .Закон
Ома для однородного участка цепи,
содержащей сопротивление R
имеет вид:
.Закон
Ома для однородного участка цепи,
содержащей сопротивление R
имеет вид:
![]() .
Если цепь разомкнута, то напряжение на
клеммах источника тока равно ЭДС:
.
Если цепь разомкнута, то напряжение на
клеммах источника тока равно ЭДС:![]() .
Эта формула значит , что при движении
положительного заряда от отрицательной
клеммы источника к положительной
сторонние силы так же совершают работу,
против сил электростатического поля.Т.о.
когда на участке АВ имеется источник с
ЭДС, разность потенциалов изменяется
скачком на величину ±
.
Эта формула значит , что при движении
положительного заряда от отрицательной
клеммы источника к положительной
сторонние силы так же совершают работу,
против сил электростатического поля.Т.о.
когда на участке АВ имеется источник с
ЭДС, разность потенциалов изменяется
скачком на величину ±![]() .
Знак выбирается в зависимости от
полярности включения источника( + по
току, а – против него)
.
Знак выбирается в зависимости от
полярности включения источника( + по
току, а – против него)
Тогда,
![]() .Эта
формула называется законом
Ома для неоднородного участка цепи.
Приравнивая
правые части формул получаем:
.Эта
формула называется законом
Ома для неоднородного участка цепи.
Приравнивая
правые части формул получаем:![]() .
Решаем это уравнение относительно I
:
.
Решаем это уравнение относительно I
:![]() -Закон Ома
для замкнутой цепи, показывает,
что сила тока в замкнутой цепи
пропорциональна ЭДС источника тока и
обратно пропорциональна общему
сопротивлению этой цепи.
-Закон Ома
для замкнутой цепи, показывает,
что сила тока в замкнутой цепи
пропорциональна ЭДС источника тока и
обратно пропорциональна общему
сопротивлению этой цепи.
Закон
Джоуля–Ленца:
![]() .Количество
теплоты, выделяемое постоянным
электрическим током в участке цепи,
равно произведению квадрата силы тока
на время его прохождения и электрическое
сопротивление этого участка цепи.
.Количество
теплоты, выделяемое постоянным
электрическим током в участке цепи,
равно произведению квадрата силы тока
на время его прохождения и электрическое
сопротивление этого участка цепи.
Плотность
тока.
Плотностью электрического тока
проводимости называется вектор
j,совпадающий
с направлением электрического тока в
рассматриваемой точке и численно равный
отношению силы тока dI
сквозь малый элемент поверхности ,
ортогональной направлению тока, к
площади dS┴
этого элемента:![]() .
Размерность А/м2
.Плотность постоянного тока одинакова
по всему сечению проводника
.
Размерность А/м2
.Плотность постоянного тока одинакова
по всему сечению проводника
![]()
В
цепи постоянного тока состоящей из с
переменной площадью поперечного сечения
![]() .
.
Закон
Ома в диф. форме
Пусть в металлическом проводнике
действует поле E=
const.
Под действием силы F=e-E
заряд e-
движется равноускоренно с ускорением
![]() и
к концу свободного пробега приобретает
скорость
и
к концу свободного пробега приобретает
скорость
![]() .
Среднее время свободного пробега
электронов
.
Среднее время свободного пробега
электронов
![]() ,
где
,
где
![]() – средняя длина свободного пробега.
Средняя скорость направленного движения
электронов
– средняя длина свободного пробега.
Средняя скорость направленного движения
электронов
![]() ,
или
,
или
![]() .Плотность
тока
.Плотность
тока
![]() .
Обозначим
.
Обозначим
![]() – удельная проводимость металла. Тогда
закон Ома примет вид
– удельная проводимость металла. Тогда
закон Ома примет вид
![]() .
.
Правила Кирхгофа справедливы для электрических контуров ,в которых есть узлы. Узлом электрической цепи называется любая точка разветвления цепи, в которой сходится не мене трёх проводников с током. Ток, входящий в узел считается положительным, а исходящий из узла – отрицательным.
Первое
правило Кирхгофа: «Алгебраическая сумма
токов, сходящихся в узле равна нулю»,
т.е.
![]() .
.
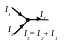
Второе
правило Кирхгофа: «В любом замкнутом
контуре, произвольно выбранном в
разветвлённой электрической цепи,
алгебраическая сумма произведений сил
токов Ii
на сопростивления Ri
соответствующих участков этого контура
равна алгебраической сумме ЭДС
![]() ,
встречающихся в этом контуре», т.е.
,
встречающихся в этом контуре», т.е.
![]() .
.
Второе правило является обобщением закона Ома на разветвленные эл. цепи.
Мощность
тока равна
работе,
которая
совершается током за единицу времени![]() Мощность Р электрического тока
– физическая
величина, равная произведению силы тока
на напряжение (по определению)
Мощность Р электрического тока
– физическая
величина, равная произведению силы тока
на напряжение (по определению)
![]() ;
;
![]() ;
;
![]() .
.
№ 20. Электромагнитное поле в вакууме и его характеристики. Электромагнитная индукция, опыт Фарадея. Правило Ленца. Самоиндукция. Принцип суперпозиции вектора магнитной индукции . Сила Лоренца, Ампера. Относительность понятий электрического и магнитного поля.
Взаимодействие между электрически заряженными частицами или телами осуществляется посредством электромагнитного поля, которое представляет собой совокупность двух взаимосвязанных поле – электрического и магнитного.
Характерная особенность электрического поля в том, что оно действует на электрический заряд (частицу или тело) с силой ,которая зависит от скорости движения зарядов. Характерная особенность магнитного поля состоит в том, что оно взаимодействует с движущимися электрическими зарядами с силой, их пропорциональной скоростям и направлению к скоростям. Электромагнитное поле в вакууме описывается напряженностью электрического поля Е и магнитной индукцией В.
Напряжённость электрического поля - векторная физическая величина (Е), являющаяся основной количественной характеристикой электрического поля; определяется отношением силы, действующей со стороны поля на электрический заряд, к величине заряда
Заряды,
создающие электростатическое поле
могут быть распределены в пространстве
дискретно или непрерывно. В первом
случае на основе принципа суперпозиции
электрических полей: напряжённость
электрического поля системы зарядов
равна геометрической сумме напряжённостей
полей создаваемых каждым зарядом в
отдельности, т.е. имеет место
![]() .
Во втором случае согласно принципу
суперпозиции
.
Во втором случае согласно принципу
суперпозиции
![]() ,
где
,
где
![]() – напряжённость поля, создаваемого в
вакууме малым зарядом
– напряжённость поля, создаваемого в
вакууме малым зарядом
![]() (интегрирование проводится по всем
непрерывно распределённым зарядам).
Интенсивность магнитного поля, т.
е.способность его производить работу,
определяется величиной, называемой
магнитной
индукцией.
Чем сильнее магнитноe поле, созданное
постоянным магнитом или электромагнитом,
тем большую индукцию оно имеет. Магнитную
индукцию В можно характеризовать
плотностью силовых магнитных линий, т.
е. числом силовых линий, проходящих
через площадь 1 м2 или 1 см2, расположенную
перпендикулярно магнитному полю.
Единицей М. и. в Международной системе
единиц служит Тесла (тл).
(интегрирование проводится по всем
непрерывно распределённым зарядам).
Интенсивность магнитного поля, т.
е.способность его производить работу,
определяется величиной, называемой
магнитной
индукцией.
Чем сильнее магнитноe поле, созданное
постоянным магнитом или электромагнитом,
тем большую индукцию оно имеет. Магнитную
индукцию В можно характеризовать
плотностью силовых магнитных линий, т.
е. числом силовых линий, проходящих
через площадь 1 м2 или 1 см2, расположенную
перпендикулярно магнитному полю.
Единицей М. и. в Международной системе
единиц служит Тесла (тл).
Электромагнитная индукция — это явление возникновения электрического тока в проводящем контре при изменении магнитного потока через поверхность, ограниченную этим контуром. Явление электромагнитной индукции было открыто Фарадеем. Он опытным путем установил, что при изменении магнитного поля внутри замкнутого проводящего контура в нем возникнет электрический ток, который называют индукционным током. Опыты Фарадея: при внесении или вынесении магнита в катушку, замкнутую на гальванометр, в катушке возникает индукционный ток. Объяснение этого явления было дано Максвеллом. Любое переменное магнитное иоле всегда порождает переменное электрическое поле.
Для количественной характеристики процесса изменения магнитного поля через замкнутый контур вводится физическая величина под названием «магнитный поток». Магнитным потоком через замкнутый контур площадью S называют физическую величину, равную произведению модуля вектора магнитной индукции В на площадь контура S и на косинус угла а между направлением вектора магнитной индукции и нормалью к площади контура. Ф = BS cos а
Опытным
путем был установлен основной закон
электромагнитной индукции: ЭДС индукции
в замкнутом контуре равна по величине
скорости изменения магнитного потока
через контур.![]() . Если рассматривать катушку, содержащую
из n
витков, то формула основного закона
электромагнитной индукции будет
выглядеть так:
. Если рассматривать катушку, содержащую
из n
витков, то формула основного закона
электромагнитной индукции будет
выглядеть так:
![]() .
Единица магнитного потока Ф — вебер
(Вб) 1 вебер — это величина такого
магнитного потока, который, уменьшаясь
до нуля за одну секунду, через замкнутый
контур наводит в нем ЭДС индукции 1 В.
.
Единица магнитного потока Ф — вебер
(Вб) 1 вебер — это величина такого
магнитного потока, который, уменьшаясь
до нуля за одну секунду, через замкнутый
контур наводит в нем ЭДС индукции 1 В.
Зависимость
направления индукционного тока от
характера изменения магнитного поля
через замкнутый контур опытным путем
установил Ленц.
Он сформулировал правило, носящее его
имя. Индукционный ток имеет такое
направление, при котором его магнитное
поле стремится скомпенсировать изменение
внешнего магнитного потока через контур.
В соответствии с правилом Ленца в законе
электромагнитной индукции должен стоять
знак минус:![]() .
.
Самоиндукция — явление возникновения ЭДС индукции в проводящем контуре при изменении электрического тока, протекающего через контур.
При изменении тока в контуре меняется магнитный поток через поверхность, ограниченную этим контуром, изменение потока магнитной индукции приводит к возбуждению ЭДС самоиндукции. Направление ЭДС оказывается таким, что при увеличении тока в цепи ЭДС препятствует возрастанию тока, а при уменьшении тока — убыванию.
Величина
ЭДС пропорциональна скорости изменения
силы тока I и индуктивности контура L:![]() .
.
Принцип
суперпозиции
магнитных полей: если магнитное поле
создано несколькими проводниками с
токами, то вектор магнитной индукции
в какой-либо точке этого поля равен
векторной сумме магнитных индукций,
созданных в этой точке каждым током в
отдельности:![]() .
.![]()
На
частицу с электрическим зарядом q,
движущуюся в магнитном поле со скоростью
v,
направленной произвольным образом по
отношению к вектору магнитной индукции
,
действует сила
Лоренца
![]() ,
или
,
или
![]() ,
где
– угол между
,
где
– угол между
![]() .
Направление силы Лоренца определяется
правилом левой руки. Сила Лоренца
перпендикулярна направлению скорости
частицы, поэтому она изменяет только
направление этой скорости. Сила действия
на заряд, на который кроме магнитного
поля с индукцией поля
действует и электрическое поле с
напряжённостью
.
Направление силы Лоренца определяется
правилом левой руки. Сила Лоренца
перпендикулярна направлению скорости
частицы, поэтому она изменяет только
направление этой скорости. Сила действия
на заряд, на который кроме магнитного
поля с индукцией поля
действует и электрическое поле с
напряжённостью
![]() ,
находится по формуле
,
находится по формуле
![]() .
.
Сила, с которой магнитное поле действует на помещенный в него проводник с током, называется силой Ампера.
Величина
этой силы, действующей на элемент Δl
проводника с током I в магнитном поле с
индукцией В , определяется законом
Ампера:
![]() ,где
α – угол между направлениями тока и
вектора индукции.
,где
α – угол между направлениями тока и
вектора индукции.
Направление силы Ампера можно найти с помощью правила левой руки:если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца совпадали по направлению с направлением тока, то отогнутый на 90° большой палец укажет направление силы, действующей на элемент проводника.
Уравнения
Максвелла инвариантны относительно
преобразований Лоренца. Электрические
заряды тел тоже не зависят от выбора
инерциальной системы отсчета. Формулы
преобразования векторов
![]() электромагнитного поля при переходе
от неподвижной инерциальной системы
отсчёта
электромагнитного поля при переходе
от неподвижной инерциальной системы
отсчёта
![]() к инерциальной системе
к инерциальной системе
![]() ,
движущейся относительно
равномерно и прямолинейно вдоль
положительного направления оси OX
со скоростью v,
имеет вид:
,
движущейся относительно
равномерно и прямолинейно вдоль
положительного направления оси OX
со скоростью v,
имеет вид:
 .
.
Из
преобразований Лоренца для электромагнитного
поля следует, что одно и то же
электромагнитное поле по-разному
проявляется в инерциальных системах
отсчёта, движущихся относительно друг
друга. В частности, если в системе отсчёта
К
есть только электрическое поле
![]() ,
а
,
а
![]() ,
то в системе отсчёта K’
будут наблюдаться и электрическое и
магнитное поля, вектор
,
то в системе отсчёта K’
будут наблюдаться и электрическое и
магнитное поля, вектор
![]() и
и
![]() которых взаимно перпендикулярны.
которых взаимно перпендикулярны.
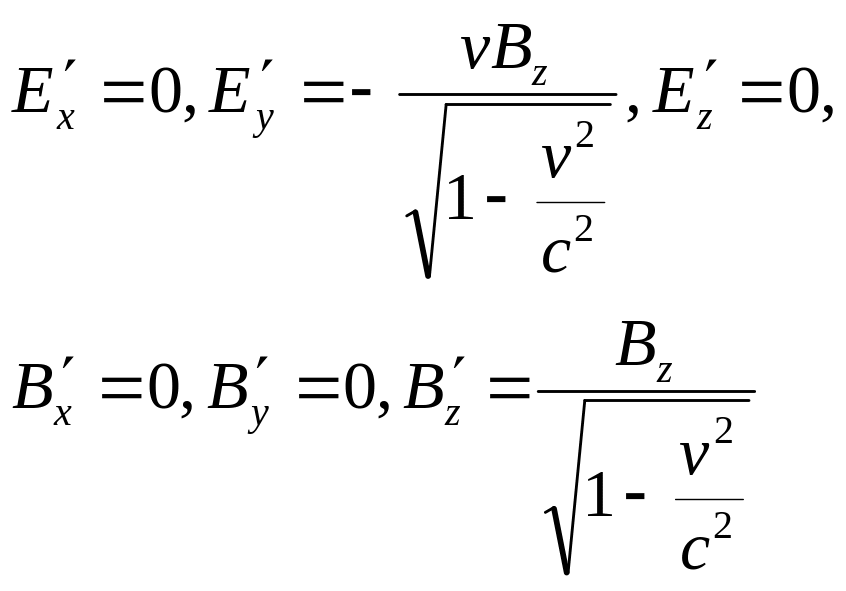 .
.
№ 21. Система уравнений Максвелла для электромагнитного поля Вихревое электрическое поле. Плотность тока смещения. Физический смысл каждого уравнения Максвелла, их основные свойства.
Для объяснения возникновения индукционного тока в неподвижных проводниках (второй опыт Фарадея) Максвелл пре6дположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в контуре (первое основное положение теории Максвелла).
Циркуляция
вектора напряженности ![]() этого поля
этого поля
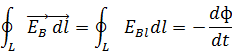
По
определению поток вектора ![]() :
Ф=
:
Ф=![]() ,
откуда следует:
,
откуда следует:

Здесь
мы используем частную производную по
времени, поскольку в общем случае
электрическое поле может быть неоднородным
и может зависеть не только от времени,
но и от координат. Таким образом,
циркуляция вектора ![]() не равна нулю, т.е. электрическое поле
,
возбуждаемое переменным магнитным
полем, как и само магнитное поле, является
вихревым.
не равна нулю, т.е. электрическое поле
,
возбуждаемое переменным магнитным
полем, как и само магнитное поле, является
вихревым.
Суммарное
электрическое поле складывается из
электрического поля, создаваемого
зарядами ![]() и вихревого электрического поля
.
Поскольку циркуляция
равна нулю, то циркуляция суммарного
поля:
и вихревого электрического поля
.
Поскольку циркуляция
равна нулю, то циркуляция суммарного
поля:
Это - первое уравнение системы уравнений Максвелла для электромагнитного поля.Максвелл предложил, что аналогично магнитному полю и всякое изменение электрического поля вызывает в окружающем пространстве вихревое магнитное поле (второе основное положение теории Максвелла).
Т.к.магнитное поле есть основной, обязательный признак всякого тока, то Максвелл назвал переменное электрическое поле током смещения. Плотность тока смещения:
![]() Открытие
тока смещения позволило Максвеллу
создать единую теорию электрических и
магнитных явлений. Основным следствием
теории Максвелла был вывод о существовании
электромагнитных волн, распространяющихся
со скоростью света в вакууме.
Открытие
тока смещения позволило Максвеллу
создать единую теорию электрических и
магнитных явлений. Основным следствием
теории Максвелла был вывод о существовании
электромагнитных волн, распространяющихся
со скоростью света в вакууме.
Система уравнений Максвелла в интегральной форме имеет вид:
1.
![]() ,
,
2.
![]() ,
,
3.
![]() ,
где
,
где
![]() – ток проводимости, а
– ток проводимости, а
![]() – ток смещения.
– ток смещения.
4.
![]() .
.
Первое уравнение связывает вектор напряжённости электрического поля с временным изменением вектора индукции магнитного поля и является выполнением закона электромагнитной индукции. Второе уравнение определяет то свойство , что его линии замкнуты или уходят в бесконечность. Третье устанавливает связь между токами проводимости и смещения и порождаемым ими магнитным полем.
Из уравнений Максвелла следует, что:
– источниками электрического поля являются либо электрические заряды, либо изменяющееся во времени магнитное поле;
– магнитные поля могут порождаться либо движущимися электрическими зарядами, либо переменным электрическим полем;
– переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т.е. они образуют единое электромагнитное поле.
Уравнения
Максвелла в дифференциальной форме
(характеризующие поле в данной точке):
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Дивергенция (скалярная величина) есть мера источника поля. Если в некоторой области дивергенция равна нулю, то векторное поле в этой точке свободно от источников. Например, уравнение – показывает, что источником поля является электрический заряд (положительный). Уравнение гворит, что не существует источников магнитного поля – «магнитных зарядов».
Ротор – есть вихрь векторного поля, поэтому первое уравнение говорит, что изменение напряженности электрического поля, порождает переменное магнитное поле.Уравнения Максвелла – наиболее общие уравнения для электрических и магнитных плей покоящихся средах.
Возникающее при изменении магнитного поля электрическое поле имеет совсем другую структуру, чем электростатическое. Оно не связано непосредственно с электрическими зарядами, и его силовые линии не могут на них начинаться и кончаться. Они вообще ни где не начинаются и нигде не кончаются, представляя собой замкнутые линии, подобные силовым линиям магнитного поля. Это так называемое вихревое поле.
№ 22. Экспериментальные основания электродинамики: взаимодействие неподвижных зарядов, опыты Кулона. Движение заряженных частиц в магнитных и электрических полях. Взаимодействие токов, опыты Ампера.
Электрический заряд – внутреннее свойство тел или частиц, характеризующее их свойство к электромагнитному взаимодействию.
Опытным путём установлено, что заряд существует двух видов: положительный и отрицательный. Одноимённые заряды отталкиваются, разноимённые – притягиваются.
В электростатике используется модель – точечный электрический заряд – заряженное тело, форма и размеры которого не существенны в данной задаче.
З акон
взаимодействия неподвижных точечных
зарядов – закон Кулона. Установлен
экспериментально. Сила взаимодействия
F
между двумя неподвижными точечными
зарядами в вакууме, пропорциональна
зарядам q1
и q2
и обратно пропорциональна квадрату
расстояния между ними, т.е.
акон
взаимодействия неподвижных точечных
зарядов – закон Кулона. Установлен
экспериментально. Сила взаимодействия
F
между двумя неподвижными точечными
зарядами в вакууме, пропорциональна
зарядам q1
и q2
и обратно пропорциональна квадрату
расстояния между ними, т.е.
![]() .
.
Сила
F
направлена по линии, соединяющей центры
зарядов, является центральной, и может
быть, как силой притяжения, так и силой
отталкивания. В векторной форме имеем
![]() ,
где
,
где
![]() – электрическая постоянная (8,85*10-12
Ф/м).
– электрическая постоянная (8,85*10-12
Ф/м).
Движение
заряженных частиц в магнитных и
электрических поляхНа
заряженную частицу в электростатическом
поле действует кулоновская сила, которую
можно найти, зная напряженность поля в
данной точке:
![]() .
Эта сила сообщает ускорение
.
Эта сила сообщает ускорение
![]() ,
где m — масса заряженной частицы. Как
видно, направление ускорения будет
совпадать с направлением
,
где m — масса заряженной частицы. Как
видно, направление ускорения будет
совпадать с направлением
![]() ,
если заряд частицы положителен (q > 0),
и будет противоположно
, если заряд отрицателен (q<0).
,
если заряд частицы положителен (q > 0),
и будет противоположно
, если заряд отрицателен (q<0).
Если
электростатическое поле однородное (
= const), то ускорение а = const и частица будет
совершать равноускоренное движение
(при отсутствии других сил). Вид траектории
частицы зависит от начальных условий.
Если вначале заряженная частица покоилась
![]() или ее начальная скорость сонаправлена
с ускорением
или ее начальная скорость сонаправлена
с ускорением
![]() ,
то частица будет совершать равноускоренное
прямолинейное движение вдоль поля и ее
скорость будет расти. Если
,
то частица будет совершать равноускоренное
прямолинейное движение вдоль поля и ее
скорость будет расти. Если
![]() ,
то частица будет тормозиться в этом
поле.
,
то частица будет тормозиться в этом
поле.
Если угол между начальной скоростью и ускорением острый О < α < 90° (или тупой), то заряженная частица в таком электростатическом поле будет двигаться по параболе.
Существенное отличие магнитного поля от электростатического состоит, во-первых, в том, что магнитное поле не действует на покоящуюся заряженную частицу. Во-вторых, сила Лоренца, действующая на заряженные частицы в магнитном поле, всегда перпендикулярна скорости их движения. Поэтому модуль скорости в магнитном поле не изменяется. Не изменяется, следовательно, и кинетическая энергия частицы. Вид траектории заряженной частицы в магнитном поле зависит от угла между скоростью влетающей в поле частицы и магнитной индукцией. Возможны три различных случая.
1.
Заряженная частица влетает в магнитное
поле со скоростью
![]() ,
направленной вдоль поля
,
направленной вдоль поля
![]() или противоположно направлению магнитной
индукции поля
или противоположно направлению магнитной
индукции поля
![]() . В этих случаях сила Лоренца
. В этих случаях сила Лоренца
![]() и частица будет продолжать двигаться
равномерно прямолинейно.
и частица будет продолжать двигаться
равномерно прямолинейно.
2.
Заряженная частица движется перпендикулярно
линиям магнитной индукции (рис. 2), тогда
сила Лоренца
![]() , а следовательно, и сообщаемое ускорение
будут постоянны по модулю и перпендикулярны
к скорости частицы. В результате частица
будет двигаться по окружности, радиус
которой можно найти на основании второго
закона Ньютона:
, а следовательно, и сообщаемое ускорение
будут постоянны по модулю и перпендикулярны
к скорости частицы. В результате частица
будет двигаться по окружности, радиус
которой можно найти на основании второго
закона Ньютона:
![]() Отношение
Отношение
![]() — называют удельным зарядом частицы.
— называют удельным зарядом частицы.
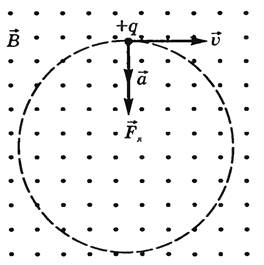
Период
вращения частицы
![]()
то есть период вращения не зависит от скорости частицы и радиуса траектории. На этом основано действие циклотрона.
3.
Скорость заряженной частицы направлена
под углом
![]() к вектору
к вектору
![]()
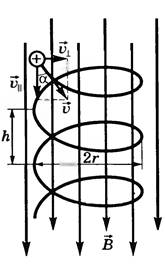
Движение
частицы можно представить в виде
суперпозиции равномерного прямолинейного
движения вдоль поля со скоростью
![]() и движения по окружности с постоянной
по модулю скоростью
и движения по окружности с постоянной
по модулю скоростью
![]() в плоскости, перпендикулярной полю.
Радиус окружности определяется аналогично
предыдущему случаю, только надо заменить
в плоскости, перпендикулярной полю.
Радиус окружности определяется аналогично
предыдущему случаю, только надо заменить
![]() на
, то есть
на
, то есть
![]()
В
результате сложения этих движений
возникает движение по винтовой линии,
ось которой параллельна магнитному
полю. Шаг винтовой линии
![]()
Направление, в котором закручивается спираль, зависит от знака заряда частицы.
Электрические токи взаимодействуют между собой. Например, два тонких прямолинейных проводника с током притягивают друг друга, если токи в них сонаправлены, и отталкивают, друг друга, если токи в них направлены противоположно.
З акон
взаимодействия токов был установлен
Ампером экспериментально. Сила
акон
взаимодействия токов был установлен
Ампером экспериментально. Сила
![]() с
которой магнитное поле действует на
элемент тока длиной dl,
находящийся в поле, равна
с
которой магнитное поле действует на
элемент тока длиной dl,
находящийся в поле, равна
![]() ,
где
– вектор магнитной индукции. Величина
силы вычисляется по формуле
,
где
– вектор магнитной индукции. Величина
силы вычисляется по формуле
![]() .
Направление силы Ампера принято
определять с помощью правила левой
руки: если ладонь левой руки расположить
так, чтобы линии вектора магнитной
индукции входили в неё, а четыре вытянутых
пальца расположить по направлению тока,
то согнутый большой палец укажет
направление силы Ампера.
.
Направление силы Ампера принято
определять с помощью правила левой
руки: если ладонь левой руки расположить
так, чтобы линии вектора магнитной
индукции входили в неё, а четыре вытянутых
пальца расположить по направлению тока,
то согнутый большой палец укажет
направление силы Ампера.
Закон
Ампера применяется для определения
силы взаимодействия токов. Два параллельных
проводника с токами I1
и I2
находятся на расстоянии d
друг от друга. Направление сил
![]() и
и
![]() ,
с которыми поля
,
с которыми поля
![]() и
и
![]() действуют на проводники определяется
по правилу левой руки. Имеем
действуют на проводники определяется
по правилу левой руки. Имеем
![]() и
и
![]() .
.
Тогда
по закону Ампера
![]() ,
здесь
,
здесь
![]() – магнитная постоянная,
– магнитная постоянная,
![]() – магнитная проницаемость среды.
– магнитная проницаемость среды.
№ 23. Колебательный контур. Свободные и вынужденные колебания. Собственная частота колебаний, коэффициент затухания. Резонанс. Генерация незатухающих электромагнитных колебаний. Переменный ток. Индуктивность, емкость и сопротивление переменного тока. Работа и мощность переменного тока.
Э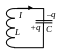 лектрическая
цепь, в которой могут происходить
электрические колебания называется
колебательным контуром. Колебательный
контур состоит из конденсатора
электроёмкостью С
и, соединённой с ним последовательно,
катушки индуктивностью L.
При замыкании на катушку предварительно
заряженного конденсатора в колебательном
контуре возникают свободные колебания
заряда обкладок конденсатора и тока в
катушке. Переменное электромагнитное
поле распространяется в пространстве
со скоростью с
– скоростью света в вакууме. При малых
линейных размерах контура можно считать,
что сила тока I
в начальный момент времени t
во всех частях контура одинакова. Такой
переменный ток называют квазистационарным.
лектрическая
цепь, в которой могут происходить
электрические колебания называется
колебательным контуром. Колебательный
контур состоит из конденсатора
электроёмкостью С
и, соединённой с ним последовательно,
катушки индуктивностью L.
При замыкании на катушку предварительно
заряженного конденсатора в колебательном
контуре возникают свободные колебания
заряда обкладок конденсатора и тока в
катушке. Переменное электромагнитное
поле распространяется в пространстве
со скоростью с
– скоростью света в вакууме. При малых
линейных размерах контура можно считать,
что сила тока I
в начальный момент времени t
во всех частях контура одинакова. Такой
переменный ток называют квазистационарным.
Дифференциальное уравнение колебаний имеет вид:
![]() .
.
Свободные электрические колебания в колебательном контуре являются гармоническими, если его электрическое сопротивление R=0:
![]() .
.
Циклическая частота и период колебаний удовлетворяют формуле Томпсона:
![]() .
.
Заряд q конденсатора и сила тока i в контуре изменяются по законам:
![]() ,
,
где
q0
– амплитуда заряда, а
![]() – амплитуда силы тока.
– амплитуда силы тока.
Разность
потенциалов обкладок конденсатора
![]() также изменяется по гармоническому
закону и совпадает по фазе с зарядом q:
также изменяется по гармоническому
закону и совпадает по фазе с зарядом q:
![]() .
Величина
.
Величина
![]() – называется волновым сопротивлением.
– называется волновым сопротивлением.
При свободных гармонических колебаниях в колебательном контуре происходят периодические преобразования энергии Wc электрического поля конденсатора в энергию Wм магнитного поля катушки индуктивности и наоборот:
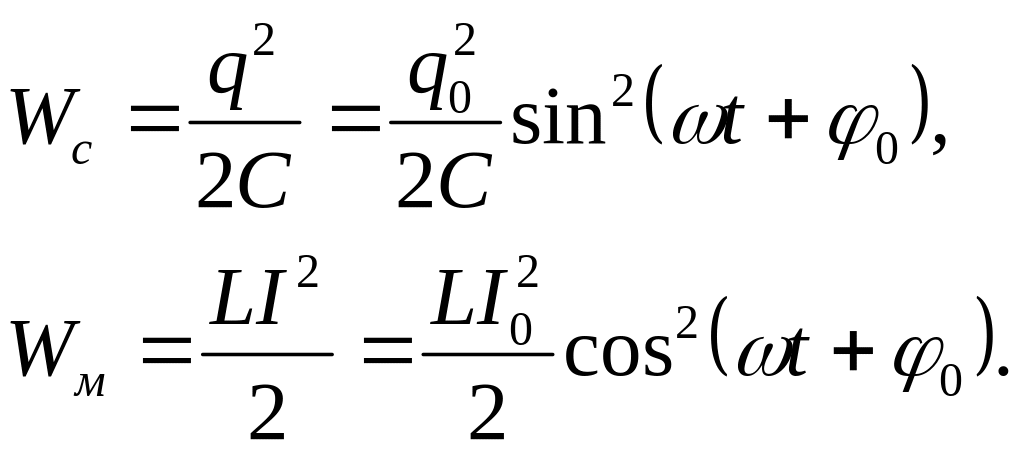
П олная
энергия электромагнитных колебаний в
контуре не изменяется с течением времени:
олная
энергия электромагнитных колебаний в
контуре не изменяется с течением времени:
![]() .
.
Для осуществления вынужденных колебаний в электрическом колебательном контуре в него необходимо включить источник электрической энергии. ЭДС которого изменяется с течением времени. Дифференциальное уравнение вынужденных колебаний в контуре имеет вид:
![]() ,
,
где
![]() – коэффициент затухания свободных
колебаний в контуре, а
– коэффициент затухания свободных
колебаний в контуре, а
![]() – циклическая частота свободных
незатухающих колебаний (при R=0).
– циклическая частота свободных
незатухающих колебаний (при R=0).
Пусть
ЭДС
![]() изменяется по закону
изменяется по закону
![]() ,
тогда при установившихся колебаниях
заряд конденсатора колеблется гармонически
с той же циклической частотой
,
тогда при установившихся колебаниях
заряд конденсатора колеблется гармонически
с той же циклической частотой
![]() :
:
![]() .
Тангенс начальной фазы
.
Тангенс начальной фазы
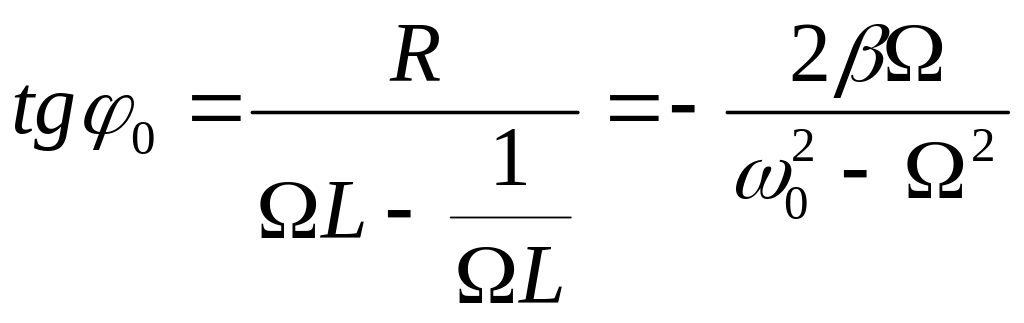 .
.
При
![]() фаза
фаза
![]() – заряд конденсатора при постоянной
разности потенциалов между обкладками,
равной
.
Сила тока установившихся вынужденных
колебаний в контуре
– заряд конденсатора при постоянной
разности потенциалов между обкладками,
равной
.
Сила тока установившихся вынужденных
колебаний в контуре
![]()
 .
.
Графики зависимости I0 от при различных значениях R, называются резонансными кривыми колебательного контура и имеют вид, указанный на рисунке.
![]() .
.
Резонансная циклическая частота Ωр, соответствующая максимуму амплитуды тока в контуре при вынужденных колебаниях, не зависит от R,
![]() .
.
Амплитуда
силы тока при резонансе
![]() .
.
В реальном колебательном контуре свободные электромагнитные колебания будут затухающими из-за потерь энергии на нагревание проводов. Для получения незатухающих электромагнитных колебаний, необходимо колебательный контур пополнять электроэнергией, чтобы скомпенсировать потери энергии. Для получения незатухающих электромагнитных колебаний применяют индукционный генератор.
Переменный
ток - вынужденные колебания в цепи,
совпадающие с частотой вынужденных
колебаний. Пусть переменная ЭДС (или
переменное напряжение) имеет вид![]()
где
Um
и Uo,
амплитуды ЭДС и напряжения.
Тогда
на участке цепи имеющей сопротивление
R, емкость C и индуктивность L дифференциальное
уравнение закона Ома имеет вид
![]() или
или
![]()
Рассмотрим частный случай цепи
1)
R
≠0,
С
→ 0, L→
0: переменная напряжения приложено к
сопротивлению
R.
Закон Ома:
![]() ,
амплитуда силы тока:
,
амплитуда силы тока:
![]()
Колебания тока происходят в одной фазе с напряжением. Векторная
![]()
2) R →0, С →0, L ≠ 0 Переменное напряжение приложено к катушке
индуктивности ЭДС самоиндукции в катушке
Закон
Ома:
![]()
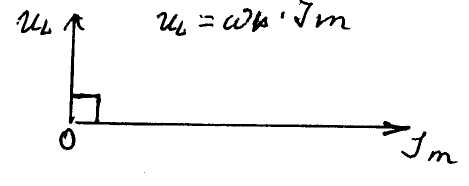
![]() где
где![]() .
Т.о. падение напряжения UL
опережает по фазе ток I
текущий через катушку на
.
Т.о. падение напряжения UL
опережает по фазе ток I
текущий через катушку на
![]() .
величина
.
величина
![]()
называется реактивным индукционным сопротивлением.
R
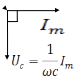 →0,
С ≠0, L→0
переменное напряжение приложено к
конденсатору
→0,
С ≠0, L→0
переменное напряжение приложено к
конденсатору
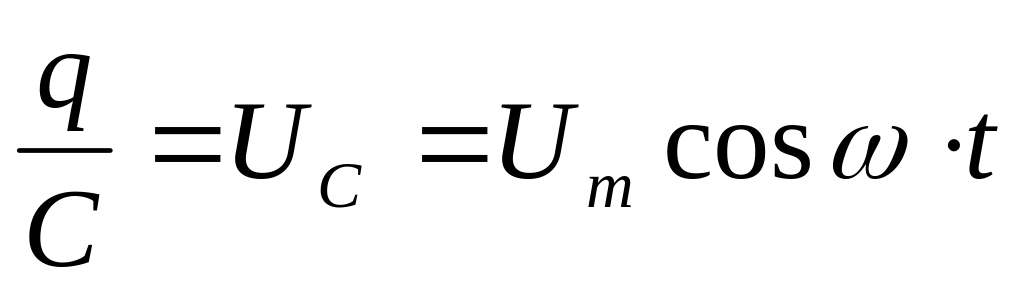 ,
,
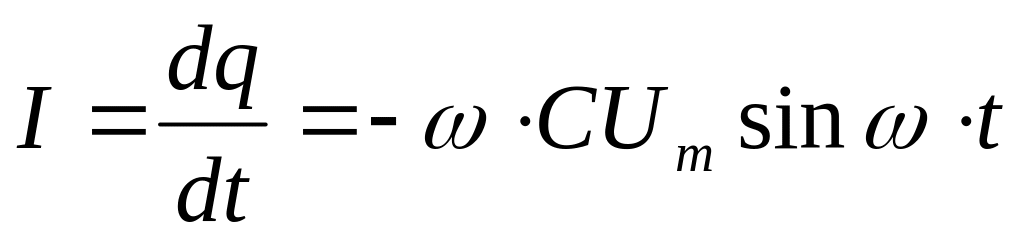 ,
,
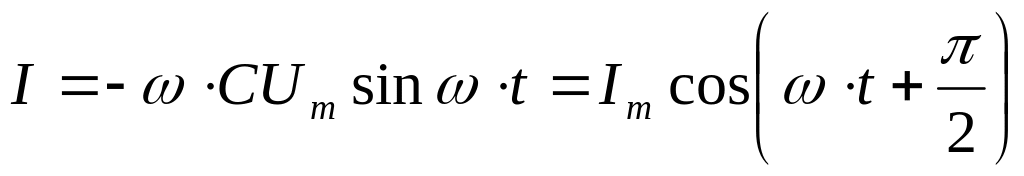 ,
где
,
где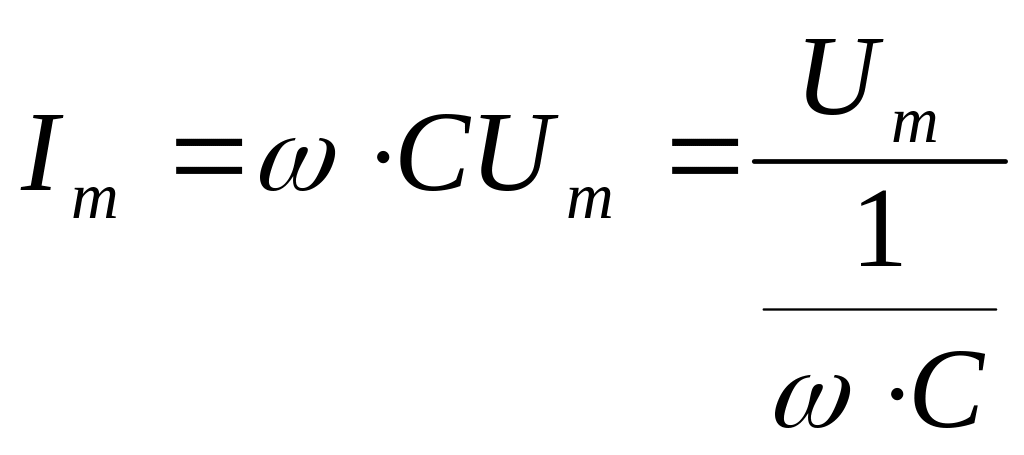 ,
величина
,
величина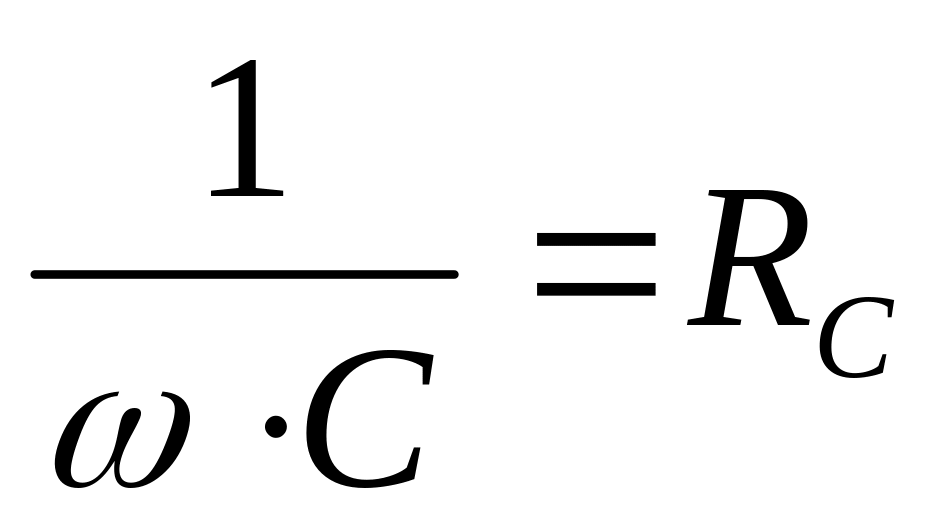
Таким образом, падение напряжение Uс отстает от текущего через конденсатор тока I на π/2.
Величина
![]() называется реактивным емкостным
сопротивлением. Для постоянного тока
(
называется реактивным емкостным
сопротивлением. Для постоянного тока
(![]() )
RC=
)
RC=![]() ,
т.е. постоянный ток через конденсатор
течь не может.
,
т.е. постоянный ток через конденсатор
течь не может.
В
общем случае, если R
≠
0,
С ≠ 0,
L
≠ 0 . Если напряжение изменяется по
закону
![]()
то
ток изменяется по
закону
![]() Где
Im
и φ
определяются формулами
Где
Im
и φ
определяются формулами
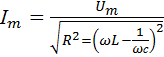

Величина
![]() -называется
полным сопротивлением
-называется
полным сопротивлением
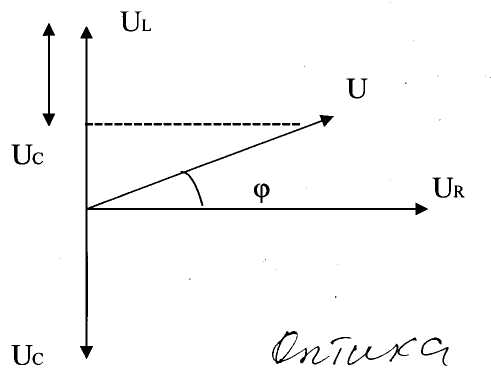
Общая векторная диаграмма имеет вид
Величина:
X=RL-RC=![]() называется реактивным сопротивлением
называется реактивным сопротивлением
![]() .
В этом случае І=
.
В этом случае І=![]() -
сила тока в цепи.
-
сила тока в цепи.
P= PR+ PL+ PC- эти мощности называют мощностью на сопротивлении, на индуктивности, на ёмкости.
Допустим,
что омическое сопротивление, индуктивность
и емкость сосредоточены на разных
участках цепи. Тогда на омическом
сопротивлении происходит изменение
потенциала на
![]() его принято называть потерей напряжения
на сопротивление. На конденсаторе
его принято называть потерей напряжения
на сопротивление. На конденсаторе
![]() ,
а на индуктивности
,
а на индуктивности
![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
следовательно,
,
следовательно,
![]() .
.
№24 Электромагнитные волны. Плотность энергии и плотность потока энергии электромагнитного поля .Вектор Умова-Пойтинга, его физический смысл Направление вектора Умова-Пойтинга относительно Е,Н. Понятие об импульсе электромагнитного поля.
Электромагнитные
волны- это переменное электромагнитное
поле, распространяющееся в пространстве
с конечной скоростью. Существование
электромагнитных волн вытекает из
уравнений Максвелла:
,
,
,
,
которые в области пространства, не
содержащей свободных электрических
зарядов и макроскопических токов , имеют
вид:
,
![]() ,
,
![]() ,
,
![]() .Если
среда- однородный и изотропный диэлектрик,
то
.Если
среда- однородный и изотропный диэлектрик,
то
![]() и
и
![]() ,
где
и
-
диэлектрическая и магнитная проницаемость
среды. В этом случае уравнения Максвелла
,
где
и
-
диэлектрическая и магнитная проницаемость
среды. В этом случае уравнения Максвелла
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Используя
,
![]() ,
получим волновые уравнения для векторов
,
получим волновые уравнения для векторов
![]() и
и
![]() .
.
![]() ,
,
![]()
![]() ,
где
,
где
![]() -
оператор Лапласа,
-
оператор Лапласа,
![]() -
фазовая скорость электромагнитной
волны.Т.о., электромагнитные поля
действительно могут существовать в
виде электромагнитных волн. Поскольку
-
фазовая скорость электромагнитной
волны.Т.о., электромагнитные поля
действительно могут существовать в
виде электромагнитных волн. Поскольку![]() , то
, то
![]() -
скорость распространения электромагнитных
волн в веществе всегда меньше чем в
вакууме.Векторы E
и H
напряженностей электрического и
магнитного полей волны взаимно
перпендикулярны и лежат в плоскости,
перпендикулярной вектору V
скорости распространения волны, причем
вектора E,H
и V
образуют правовинтовую систему. Взаимно
перпендикулярные векторы Е и Н колеблются
в одной фазе (их колебания синфазные).
Модули этих векторов связаны
соотношением:
-
скорость распространения электромагнитных
волн в веществе всегда меньше чем в
вакууме.Векторы E
и H
напряженностей электрического и
магнитного полей волны взаимно
перпендикулярны и лежат в плоскости,
перпендикулярной вектору V
скорости распространения волны, причем
вектора E,H
и V
образуют правовинтовую систему. Взаимно
перпендикулярные векторы Е и Н колеблются
в одной фазе (их колебания синфазные).
Модули этих векторов связаны
соотношением:![]() которое
справедливо для любой бегущей
электромагнитной волны независимо от
формы ее волновых поверхностей.
которое
справедливо для любой бегущей
электромагнитной волны независимо от
формы ее волновых поверхностей.
Объемная плотность энергии электромагнитного поля равна сумме объемных плотностей энергии электрического и магнитного полей. Для поля в линейной изотропной среде
![]()
где
![]() -относительные
диэлектрическая и магнитная проницаемость
среды, Е, Н - напряженности электрического
и магнитного полей.
-относительные
диэлектрическая и магнитная проницаемость
среды, Е, Н - напряженности электрического
и магнитного полей.
Из
соотношения между модулями векторов Е
и Н :![]() поле электромагнитных волн следует,
что объемная
плотность энергии электромагнитных
волн
поле электромагнитных волн следует,
что объемная
плотность энергии электромагнитных
волн![]() ,
где v
скорость электромагнитной волы в среде
,
где v
скорость электромагнитной волы в среде
![]() .
.
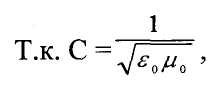
где εо и μо - электрическая и магнитная постоянные, С-
скорость электромагнитных волн в вакууме.
Вектор плотности потока электромагнитной волны называется вектором
Умова
— Пойтинга Р.
Скорость переноса энергии бегущей
монохроматической волны равна фазовой
скорости этой волны. Согласно формулам:![]() V-
вектор скорости волны,
V-
вектор скорости волны,
Поэтому
вектор Умова - Пойтинга равен![]()
Модуль
вектора Умова-Пойтинга численно равен
энергии, переносимой волной за 1 секунду
через единичную площадь поверхности,
перпендикулярной к направлению
распространения волны.![]()
Направление вектора P совпадает с направлением распространения плоской монохроматической электромагнитной волны.
В
случае плоской линейной поляризованной
монохроматической волны вектор Умова
- Пойтинга направлен в сторону
распространения волны и численно равен![]()
Электромагнитное
поле, как и любой другой материальный
объект, обладает импульсом,
который легко можно найти, проинтегрировав
вектор Пойнтинга по объёму:![]()
№25 Геометрическая оптика. Приближение коротких волн. Основные понятия и законы геометрической оптики. Зеркала, линзы, призмы. Формула тонкой линзы, абберации. Световые величины в фотометрии. Оптические приборы.
Геометрическая оптика - раздел физики, который изучает природу света, закономерностей его излучения, распространения и взаимодействие с веществом. Для характеристики распространения волны вводятся следующие понятия:
а) Волновая поверхность - поверхность всех точек, которое волновое возмущение достигает в один и тот же момент времени.
б) Луч - это геометрическая линия, проведённая перпендикулярно волновой поверхности, показывающая направление распространения волнового возмущения.
Еще до установление природы света были известны следующие законы:
Закон прямолинейного распространения света – свет в оптически однородной среде распространяется прямолинейно.
Закон независимости световых пучков- эффект производимый отдельным пучком, не зависит от того, действуют ли одновременно остальные пучки или они устранены.
Закон
отражения- отраженный луч лежит в одной
плоскости с падающим лучом и
перпендикуляром , проведенным к границе
раздела двух сред в точке падения: угол
отражения равен углу падения:![]()
Закон
преломления- падающий и преломленный
лучи, а также перпендикуляр к границе
раздела двух сред, восстановленный в
точке падения луча, лежат в одной
плоскости. Отношение синуса угла падения
α к синусу угла преломления β есть
величина, постоянная для двух данных
сред:![]() ,
где
,
где
![]() -
относительный показатель преломления
второй среды относительно первой,
Относительный
показатель преломления двух сред равен
отношению их абсолютных показателей
преломления: n12
= n2 / n1. Следовательно, закон преломления
будет иметь вид:
-
относительный показатель преломления
второй среды относительно первой,
Относительный
показатель преломления двух сред равен
отношению их абсолютных показателей
преломления: n12
= n2 / n1. Следовательно, закон преломления
будет иметь вид:
![]()
А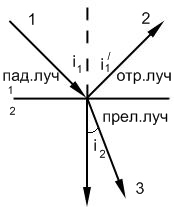 бсолютным
показателем преломления среды называется
величина n,равная
отношению скорости электромагнитных
волн в вакууме с к их фазовой скорости
v
в среде:
бсолютным
показателем преломления среды называется
величина n,равная
отношению скорости электромагнитных
волн в вакууме с к их фазовой скорости
v
в среде:![]() , т.к.
,
то
, т.к.
,
то
![]()
Простейшим оптическим устройством, способным создавать изображение предмета, является плоское зеркало. Изображение предмета формируется за счет лучей , отраженных от зеркальной поверхности. Это изображение является мнимым, т.к. оно образуется пересечением не самих отраженных лучей , а их продолжений в зазеркалье. вследствие закона отражения света мнимое изображение предмета располагается симметрично относительно зеркальной поверхности.. Размер изображения равен размеру самого предмета.
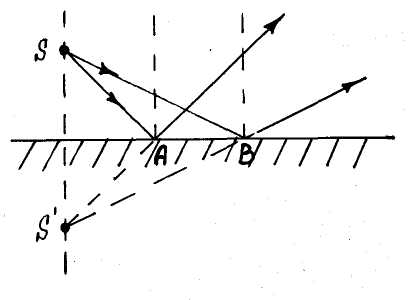
Пусть пучок лучей от точечного источника S падает на плоское зеркало. Для построения изображения возьмём два произвольных луча SA и SB. Каждый из них отражается по закону отражения. Угол между отражёнными лучами остаётся неизменным. Точка пересечения S ' продолжений лучей будет лежать на той же нормали к зеркалу, что и S и на том же расстоянии от плоскости зеркала. Изображение S' будет мнимым, симметричным.
Сферическое зеркало. Сферическим зеркалом называют зеркально отражающую поверхность , имеющую форму сферического сегмента. Центр сферы из которой вырезан сегмент , называют оптическим центром зеркала. Вершину сферического сегмента называют полюсом. Прямая. проходящая через оптической центр и полюс зеркала, называется главной оптической осью сферического зеркала .Главная оптическая ось выделена из всех других прямых , проходящих через оптический центр , только тем, что она является осью симметрии зеркала. Сферические зеркала бывают вогнутыми и выпуклыми. Если на вогнутое сферическое зеркало падает пучок лучей, параллельный главной оптической оси, то после отражения от зеркала, лучи пересекутся в точке, которая называется главным фокусом зеркала F. Расстояние от фокуса до полюса зеркала называют фокусным расстоянием и обозначают той же буквой F. У вогнутого сферического зеркала главный фокус действительный. Он расположен посередине между центром и полюсом зеркала.
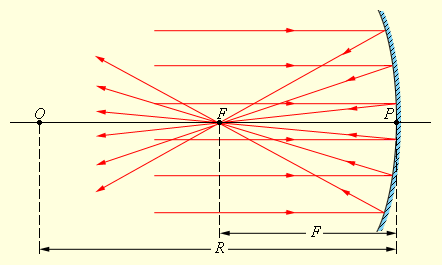
![]()
Главный
фокус выпуклого зеркала является мнимым.
Если на выпуклое зеркало падает пучок
лучей, параллельных главной оптической
оси, то после отражения в фокусе
пересекутся не сами лучи, а их продолжения.
Фокусным
расстояниям сферических зеркал
приписывается определенный знак: для
вогнутого зеркала
![]() ,для
выпуклого
,для
выпуклого![]() где R – радиус кривизны зеркала.
где R – радиус кривизны зеркала.
Для
построения изображения точки необходимо
не менее двух лучей.Для
выполнения расчетов можно пользоваться
формулой
![]() ,
где F
= R/2
- фокусное расстояние зеркала, d
- расстояние от предмета до зеркала, f
– расстояние от зеркала до изображения.
Величины
d и f подчиняются определенному правилу
знаков:
,
где F
= R/2
- фокусное расстояние зеркала, d
- расстояние от предмета до зеркала, f
– расстояние от зеркала до изображения.
Величины
d и f подчиняются определенному правилу
знаков:
d > 0 и f > 0 – для действительных предметов и изображений;
d < 0 и f < 0 – для мнимых предметов и изображений.
Линейное увеличение сферического зеркала Γ определяется как отношение линейных размеров изображения h' и предмета h.
ЛинзыЛинзы - прозрачные тела, имеющие сферические поверхности: Рассеивающие линзы(вогнутые), собирающие(двояковыпуклые или плосковыпуклые)
Собирающая линза в средней части толще и отклоняет лучи к оптической оси, если показатель преломления линзы больше показателя преломления среды.
Рассеивающая линза в средней части тоньше и отклоняет лучи от оптической оси.
1.Прямая проходящая через центр кривизны поверхностей линзы называется главной оптической осью.
2.Оптическим центром линзы называется точка , лежащая на главной оптической оси и обладающая тем свойством , что лучи проходят сквозь нее не преломляясь.
3. Побочными оптическими осями называются прямые, проходящие через оптический центр линзы и не совпадающие с главной оптической осью.
4. Фокусом линзы F называется точка, лежащая на главной оптической оси, в которой пересекаются лучи приосевого светового пучка, распространяющиеся параллельно главной оптической оси.
5. Фокальной плоскостью называется плоскость, проходящая через фокус линзы перпендикулярно ее главной оптической оси.
6.
фокусным расстоянием f
называется расстояние между оптическим
центром линзы О и ее фокусом F
:
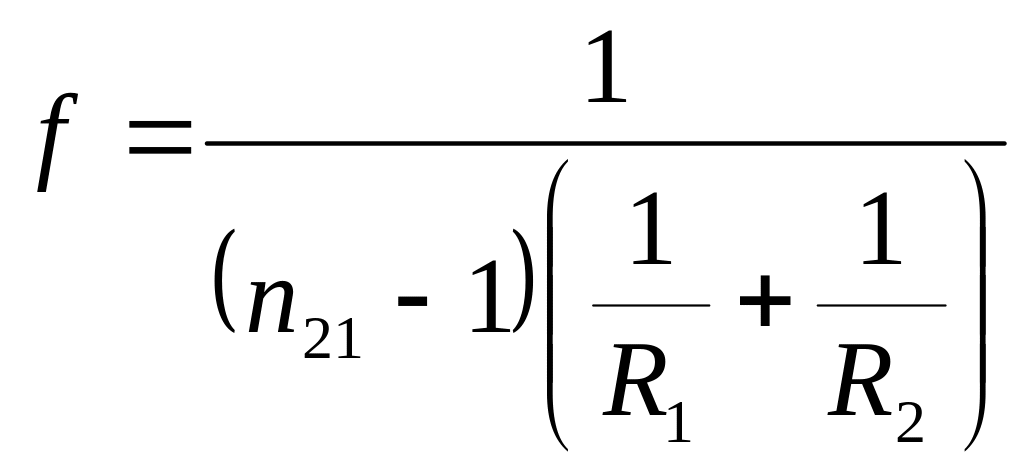
Ф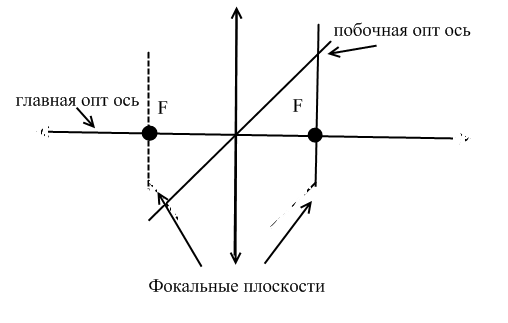 ормула
тонкой линзы: 1/F=1/d+1/f
где: F
- фокус линзы,
ормула
тонкой линзы: 1/F=1/d+1/f
где: F
- фокус линзы,
d - расстояние от предмета до линзы, f- расстояние изображения от линзы.
Для построения изображения пользуются тремя „замечательными лучами".
Л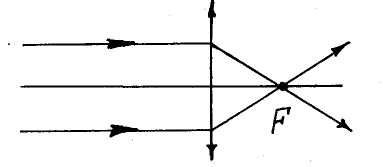 уч
параллельно главной оптической оси
преломляясь
проходит через фокус;
уч
параллельно главной оптической оси
преломляясь
проходит через фокус;
Л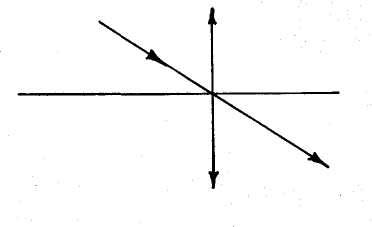 уч,
проходящий через центр линзы, не
преломляется;
уч,
проходящий через центр линзы, не
преломляется;
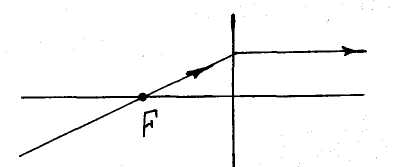 Луч,
проходящий через фокус, преломляется
параллельно главной оптической оси.
Луч,
проходящий через фокус, преломляется
параллельно главной оптической оси.
Построим изображение предмета в линзе.
Изображение перевёрнутое, действительное и уменьшенное.
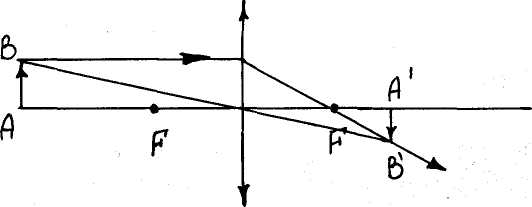 Искажения
возникающие при формировании изображения
называются абберациями. Сферическая
абберация проявляется в том , что в
случае широких световых пучков лучи
далекие от оптической оси пересекают
ее не в фокусе. Изображение удаленного
точечного источника, создаваемое широким
пучком лучей, преломленных линзой,
оказывается размытым. Хроматическая
абберация возникает вследствие того,
что показатель преломления материала
линзы зависит от длины волны света
.
Это свойство прозрачных сред называется
дисперсией. Фокусное расстояние линзы
оказывается различным для света с
разными длинами волн, что приводит к
размытию изображения при использовании
немонохрамотического света. Призма
Искажения
возникающие при формировании изображения
называются абберациями. Сферическая
абберация проявляется в том , что в
случае широких световых пучков лучи
далекие от оптической оси пересекают
ее не в фокусе. Изображение удаленного
точечного источника, создаваемое широким
пучком лучей, преломленных линзой,
оказывается размытым. Хроматическая
абберация возникает вследствие того,
что показатель преломления материала
линзы зависит от длины волны света
.
Это свойство прозрачных сред называется
дисперсией. Фокусное расстояние линзы
оказывается различным для света с
разными длинами волн, что приводит к
размытию изображения при использовании
немонохрамотического света. Призма
П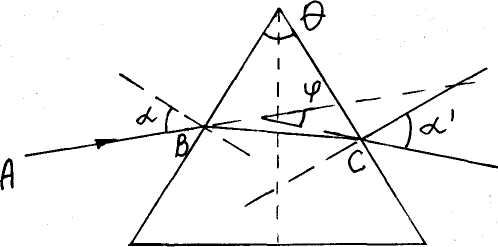 усть
луч АВ падает на одну из граней призмы.
Преломившись в точке В, луч пойдёт по
направлению ВС и преломившись в точке
С, выйдет из призмы в воздух. Найдём угол
ф, на который отклоняется луч от
первоначального направления. Угол
φ
- угол отклонения. Угол φ
= α
+ α'
-θ
где:
α
- угол падения,
усть
луч АВ падает на одну из граней призмы.
Преломившись в точке В, луч пойдёт по
направлению ВС и преломившись в точке
С, выйдет из призмы в воздух. Найдём угол
ф, на который отклоняется луч от
первоначального направления. Угол
φ
- угол отклонения. Угол φ
= α
+ α'
-θ
где:
α
- угол падения,
α' - угол выхода луча из призмы, θ - преломляющий угол призмы.
Окончательная формула имеет вид: φ = (n- 1)θ где: n - показатель преломления призмы.
Световые
величины в фотометрии. Основной
световой единицей в СИ является единица
света I
кандела-сила света в заданном направлении
источника, испускающего монохрамотическое
излучение частотой 540*1012
Гц. Световой
поток
— физическая величина, характеризующая
«количество» световой энергии в
соответствующем потоке излучения.
Освещённость
— физическая величина, численно равная
световому потоку, падающему на единицу
поверхности:![]() .Единицей
измерения освещённости в системе СИ
служит люкс.
.Единицей
измерения освещённости в системе СИ
служит люкс.
Лупа
.Простейшим
прибором для визуальных наблюдений
является лупа. Лупой называют собирающую
линзу с малым фокусным расстоянием(
F=10
см)Лупу располагают близко к глазу, а
рассматриваемый предмет –в ее фокальной
плоскости. Предмет виден через лупу под
углом
![]() ,где
h-размер
предмета. При рассмотрении этого же
предмета не вооруженным глазом его
следует расположить на расстоянии d0=25
см наилучшего зрения нормального глаза.
Предмет будет виден под углом
,где
h-размер
предмета. При рассмотрении этого же
предмета не вооруженным глазом его
следует расположить на расстоянии d0=25
см наилучшего зрения нормального глаза.
Предмет будет виден под углом
![]() .
Отсюда следует что угловое увеличение
лупы равно
.
Отсюда следует что угловое увеличение
лупы равно![]() .
Микроскоп
применяют
для получения больших увеличений при
наблюдении мелких предметов.Увеличеное
изображение предмета получается с
помощью оптической системы: две
короткофокусные линзы-объектив и окуляр.
Телескоп
предназначен
для наблюдения удаленных объектов. Они
состоят из двух линз- обращенной к
предмету собирающей линзы с большим
фокусным расстоянием(объектив) и линзы
с малым фокусным расстоянием (окуляр),
обращенной к наблюдателю. Зрительные
трубы бывают 2 типов:
зрительная
труба с собирающим (положительным)
окуляром называется трубой Кеплера,
труба с рассеивающим (отрицательным)
окуляром — трубой Галилея.
.
Микроскоп
применяют
для получения больших увеличений при
наблюдении мелких предметов.Увеличеное
изображение предмета получается с
помощью оптической системы: две
короткофокусные линзы-объектив и окуляр.
Телескоп
предназначен
для наблюдения удаленных объектов. Они
состоят из двух линз- обращенной к
предмету собирающей линзы с большим
фокусным расстоянием(объектив) и линзы
с малым фокусным расстоянием (окуляр),
обращенной к наблюдателю. Зрительные
трубы бывают 2 типов:
зрительная
труба с собирающим (положительным)
окуляром называется трубой Кеплера,
труба с рассеивающим (отрицательным)
окуляром — трубой Галилея.
№ 26. Взаимодействие света со средой: отражение и преломление . Относительный коэффициент преломления .Полное внутреннее отражение. Рассеивание света. Поляризация света. Естественный и поляризованный свет. Закон Малюса.
Закон отражения- отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром , проведенным к границе раздела двух сред в точке падения: угол отражения равен углу падения:
Закон преломления- падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения α к синусу угла преломления β есть величина, постоянная для двух данных сред: , где - относительный показатель преломления второй среды относительно первой, Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления: n12 = n2 / n1.
Следовательно, закон преломления будет иметь вид:
Абсолютным показателем преломления среды называется величина n,равная отношению скорости электромагнитных волн в вакууме с к их фазовой скорости v в среде: , т.к. , то
Если
свет распространяется из среды с большим
показателем преломления
![]() (оптически
более плотную) в среду с меньшим
показателем преломления
(оптически
более плотную) в среду с меньшим
показателем преломления
![]() (оптически
менее плотную).(
(оптически
менее плотную).(![]() )(
например из стекла в воздух, или из воды
в воздух), то
)(
например из стекла в воздух, или из воды
в воздух), то
![]() .
Следовательно, угол преломления
.
Следовательно, угол преломления![]() больше угла падения
больше угла падения![]() .
Увеличивая угол падения, при некотором
предельном угле
.
Увеличивая угол падения, при некотором
предельном угле![]() угол преломления окажется равным
угол преломления окажется равным
![]() .
При углах падения
.
При углах падения
![]() весь падающий свет полностью отражается.
При углах падения
весь падающий свет полностью отражается.
При углах падения![]() луч не преломляется, а полностью
отражается в первую среду, причем
интенсивности лучей одинаковы. Это
явление называется полным внутренним
отражением света. Предельный угол
определяется соотношением:
луч не преломляется, а полностью
отражается в первую среду, причем
интенсивности лучей одинаковы. Это
явление называется полным внутренним
отражением света. Предельный угол
определяется соотношением:![]()
П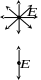 ри
действии света на вещество основное
значение имеет электрическая составляющая
электромагнитного поля световой волны,
т.к. она оказывает основное действие на
электроны в атомах вещества. Для описания
закономерностей поляризации рассматривается
только световой вектор – вектор
напряжённости
электрического поля. Свет представляет
собой суммарное электромагнитное
излучение множества независимо излучающих
атомов. Поэтому все ориентации вектора
равновероятны. Такой свет называется
естественным.
ри
действии света на вещество основное
значение имеет электрическая составляющая
электромагнитного поля световой волны,
т.к. она оказывает основное действие на
электроны в атомах вещества. Для описания
закономерностей поляризации рассматривается
только световой вектор – вектор
напряжённости
электрического поля. Свет представляет
собой суммарное электромагнитное
излучение множества независимо излучающих
атомов. Поэтому все ориентации вектора
равновероятны. Такой свет называется
естественным.
Поляризованным
светом называется свет, в котором
направление колебания вектора
каким-либо образом упорядочены. Плоско
поляризованный свет – свет, в котором
вектор
колеблется только в одной, проходящей
через луч, плоскости. Эта плоскость
называется плоскостью поляризации.
Степенью поляризации называется величина
![]() ,
где
,
где
![]() и
и
![]() – соответственно максимальная и
минимальная интенсивности частично
поляризованного света. Для естественного
света
– соответственно максимальная и
минимальная интенсивности частично
поляризованного света. Для естественного
света
![]() и
и
![]() ,
для плоскопараллельного света
,
для плоскопараллельного света
![]() .
Естественный свет можно преобразовать
в плоско поляризованный с помощью
поляризатора, пропускающего колебания
только определённого направления.
.
Естественный свет можно преобразовать
в плоско поляризованный с помощью
поляризатора, пропускающего колебания
только определённого направления.
З
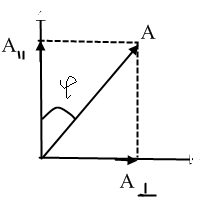 акон
Малюса.
Если пропустить естественный свет с
интенсивностью
акон
Малюса.
Если пропустить естественный свет с
интенсивностью
![]() через поляризатор
через поляризатор
![]() ,
то колебания амплитуды
,
то колебания амплитуды
![]() ,
совершающееся в плоскости, образующей
с плоскостью поляризатора угол
,
совершающееся в плоскости, образующей
с плоскостью поляризатора угол
![]() ,
можно разложить на два колебания с
амплитудами
,
можно разложить на два колебания с
амплитудами
![]() .
Интенсивность прошедшей волны
.
Интенсивность прошедшей волны
![]() .
В естественном свете все значения
равновероятны, поэтому доля света,
прошедшего через поляризатор будет
равна среднему значению
.
В естественном свете все значения
равновероятны, поэтому доля света,
прошедшего через поляризатор будет
равна среднему значению
![]() ,
а интенсивность плоско поляризованного
света, прошедшего через поляризатор
:
,
а интенсивность плоско поляризованного
света, прошедшего через поляризатор
:
![]() .
.
Если
поставить на пути плоскополяризованного
света второй поляризатор
![]() (анализатор) под углом
к первому. Интенсивность I
света, прошедшего через анализатор
меняется в зависимости от угла
по закону Малюса
(анализатор) под углом
к первому. Интенсивность I
света, прошедшего через анализатор
меняется в зависимости от угла
по закону Малюса
![]() .
Следовательно, интенсивность сета,
прошедшего через оба поляризатора
.
Следовательно, интенсивность сета,
прошедшего через оба поляризатора
![]() .
Откуда
.
Откуда
![]() ,
когда поляризаторы параллельны, и
,
когда поляризаторы параллельны, и
![]() ,
когда поляризаторы скрещены.
,
когда поляризаторы скрещены.
Е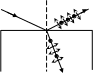 сли
естественный свет падает на границу
раздела двух диэлектриков, то отражённый
и преломлённый лучи являются частично
поляризованными. В отражённом луче
преобладают колебания перпендикулярные
плоскости падения, а в преломлённом –
колебания, лежащие в плоскости падения.
сли
естественный свет падает на границу
раздела двух диэлектриков, то отражённый
и преломлённый лучи являются частично
поляризованными. В отражённом луче
преобладают колебания перпендикулярные
плоскости падения, а в преломлённом –
колебания, лежащие в плоскости падения.
Если
угол падения равен углу Брюстера, который
определяется соотношением
![]() ,
то отражённый луч является
плоскополяризованным. Преломлённый
луч в этом случае поляризуется максимально,
но не полностью. При этом отражённый и
преломлённый лучи взаимно перпендикулярны.
,
то отражённый луч является
плоскополяризованным. Преломлённый
луч в этом случае поляризуется максимально,
но не полностью. При этом отражённый и
преломлённый лучи взаимно перпендикулярны.
№27. Дифракция света. Принцип Гюйгенса-Френеля и его приложение к решению дифракционных задач. Дифракция Фраунгофера, Френеля. Дифракционная решетка. Условия дифракции, разрешающая способность решетки.
Дифракцией называется огибание волнами препятствий, встречающихся на пути. Согласно принципу Гюйгенса-Френеля световая волна, возбуждаемая каким либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, излучаемых бесконечно малыми элементами любой замкнутой поверхности, охватывающей источник S.
Найдем в произвольной точке М амплитуду световой волны, распространяющейся в однородной среде из точечного источника S
Ф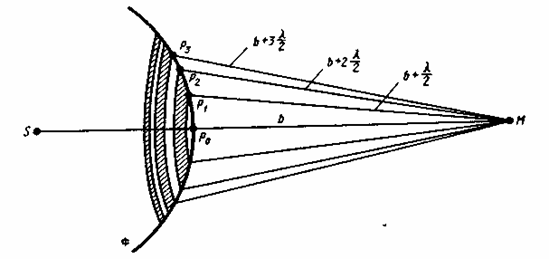 ренель
разбил волновую поверхность Ф на
кольцевые зоны такого размера, чтобы
расстояния от краев зоны до М отличались
на λ/2. Т. к. колебания от соседних зон
проходят до точки М расстояния,
отличающиеся на λ/2, то в точку М они
приходят в противоположной фазе и при
наложении эти колебания будут взаимно
ослаблять друг друга. Поэтому амплитуда
результирующего светового колебания
в точке М: А=А1-А2+А3-А4+….
ренель
разбил волновую поверхность Ф на
кольцевые зоны такого размера, чтобы
расстояния от краев зоны до М отличались
на λ/2. Т. к. колебания от соседних зон
проходят до точки М расстояния,
отличающиеся на λ/2, то в точку М они
приходят в противоположной фазе и при
наложении эти колебания будут взаимно
ослаблять друг друга. Поэтому амплитуда
результирующего светового колебания
в точке М: А=А1-А2+А3-А4+….
где А1, А2, ... - амплитуды колебаний, возбуждаемых 1-й, 2-й, ..., m-й зонами.
При
таком разбиении волновой поверхности
на зоны оказывается , что амплитуда
колебания Аm
равна среднему арифметическому от
амплитуды, примыкающей к ней зон
![]() .
Тогда результирующая амплитуда в точке
М будет равна
.
Тогда результирующая амплитуда в точке
М будет равна
![]()
т.
к. выражения, стоящие в скобках равны
нулю, а оставшаяся часть от амплитуды
последней зоны ± Аm/2 ничтожно мала.
Площадь всех зон Френеля равна![]() ,
где а-длина отрезка SP0-радиус
сферы Ф. b-
длина отрезка P0M.
,
где а-длина отрезка SP0-радиус
сферы Ф. b-
длина отрезка P0M.
Радиус
внешней границы m-й
зоны Френеля
![]() .Следовательно,
распространение света от S к М происходит
прямолинейно. Т.о., принцип Гюйгенса -
Френеля позволяет объяснить прямолинейное
распространение света в однородной
среде.
.Следовательно,
распространение света от S к М происходит
прямолинейно. Т.о., принцип Гюйгенса -
Френеля позволяет объяснить прямолинейное
распространение света в однородной
среде.
Дифракция
в сходящихся лучах( дифракция Френеля)
–это дифракция сферических волн,
осуществляемая в том случае, когда
дифракционная картина наблюдается на
конечном расстоянии от препятствия,
вызвавшего дифракцию.
Дифракция
на круглом отверстии.
Сферическая волна, распространяющаяся
из точечного источника S, встречает на
своем пути экран с круглым отверстием.
Вид дифракционной картины зависит от
числа зон Френеля, укладывающихся в
отверстии. Амплитуда результирующего
колебания, возбуждаемого в точке В всеми
зонами будет![]() ,где
знак плюс соответствует нечетным m и
минус - четным m.
,где
знак плюс соответствует нечетным m и
минус - четным m.
Д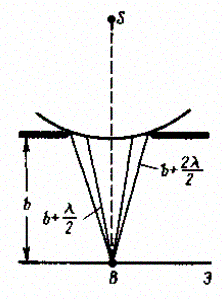 ифракционная
картина будет иметь вид чередующихся
темных и светлых колец с центром в точке
В( если m-четное,
то центральное кольцо темное, если m
нечетное, то – светлое.
ифракционная
картина будет иметь вид чередующихся
темных и светлых колец с центром в точке
В( если m-четное,
то центральное кольцо темное, если m
нечетное, то – светлое.
Дифракция
на диске. Сферическая волна,
распространяющаяся от точечного
источника S, встречает на своем пути
диск.
Пусть
диск закрывает m
первых зон Френеля. Тогда амплитуда
результирующего колебания в точке В
равна:![]() Следовательно,
в точке В всегда наблюдается
интерференционный максимум (светлое
пятно), соответствующий половине действия
первой открытой зоны Френеля. Центральный
максимум окружен концентрическими с
ним темными и светлыми кольцами.
Следовательно,
в точке В всегда наблюдается
интерференционный максимум (светлое
пятно), соответствующий половине действия
первой открытой зоны Френеля. Центральный
максимум окружен концентрическими с
ним темными и светлыми кольцами.
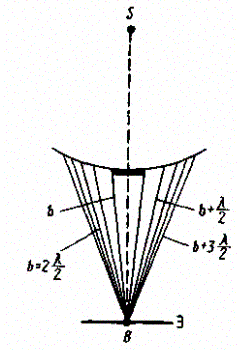
Фраунгофер
рассмотрел дифракцию плоских световых
волн, или дифракцию в параллельных
лучах.
Дифракция
Фраунгофера наблюдается в том случае,
когда источник света и точка наблюдения
бесконечно удалены от препятствия,
вызвавшего дифракцию. Чтобы этот тип
дифракции осуществить, достаточно
точечный источник света поместить в
фокусе собирающей линзы, а дифракционную
картину исследовать в фокальной плоскости
второй собирающей линзы, установленной
за препятствием.
Рассмотрим дифракцию Фраунгофера от
бесконечно длинной щели. Пусть плоская
монохроматическая световая волна падает
нормально плоскости узкой щели шириной
а=MN.Оптическая
разность хода между МС и ND:![]() ,
где F- основание перпендикуляра,
опущенного из точки М на луч ND.
,
где F- основание перпендикуляра,
опущенного из точки М на луч ND.
Разобьем открытую часть волновой поверхности в плоскости щели MN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна λ/2, т. е. всего на ширине щели уместится Δ:λ/2 зон.
В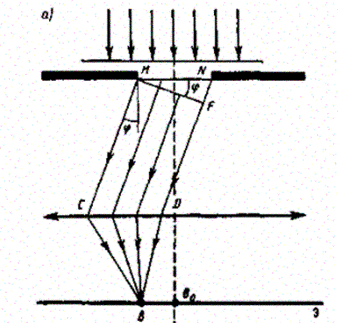 се
точки волнового фронта в плоскости щели
будут колебаться в одинаковой фазе.
Амплитуды вторичных волн в плоскости
щели будут равны, так как выбранные зоны
Френеля имеют одинаковые площади и
одинаково наклонены к направлению
наблюдения. Поэтому суммарная интенсивность
колебаний от двух любых соседних зон
Френеля равна нулю. Следовательно, если
число зон Френеля четное,
то
се
точки волнового фронта в плоскости щели
будут колебаться в одинаковой фазе.
Амплитуды вторичных волн в плоскости
щели будут равны, так как выбранные зоны
Френеля имеют одинаковые площади и
одинаково наклонены к направлению
наблюдения. Поэтому суммарная интенсивность
колебаний от двух любых соседних зон
Френеля равна нулю. Следовательно, если
число зон Френеля четное,
то![]() (m=1,2,3…..)-дифракционный
минимум (полная темнота). Если число
зон Френеля нечетное, то
(m=1,2,3…..)-дифракционный
минимум (полная темнота). Если число
зон Френеля нечетное, то![]() -дифракционный
максимум.
-дифракционный
максимум.
Одномерная дифракционная решетка – система параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равным по ширине непрозрачными промежутками.
В дифракционной решетке осуществляется многолучевая интерференция когерентных пучков света, идущих от всех щелей.
Если
а- ширина каждой щели; b- ширина между
непрозрачными участками между щелями,
то величина d=b+а называется постоянной
(периодом) дифракционной решетки.d=![]() .
где - число щелей, приходящееся на
единицу длины.
.
где - число щелей, приходящееся на
единицу длины.
Разность
хода лучей, идущих от двух соседних
щелей, будут для данного направления φ
одинаковы в пределах всей дифракционной
решетки:![]()
Если
решетка состоит из N щелей, то: Условие
главных максимумов:
![]() ,
Условие главных минимумов:
,
Условие главных минимумов:
![]()
Положение главных максимумов зависит от длины волны λ, поэтому при пропускании через решетку белого света все максимумы, кроме центрального (m=0), разложатся в спектр, фиолетовая область будет обращена к центру картины , красная – наружу. Поэтому диф. решетка может быть использована как спектральный прибор.
Разрешающей способностью спектрального прибора называют безразмерную величину R=, где - абсолютное значение минимальной разности длин волн двух соседних спектральных линий, при которой эти линии регистрируются отдельно.
Разрешающая
способность диф. решетка пропорциональна
порядку спектра m
и числу щелей N:
![]()
№28 Дисперсия света. Нормальная дисперсия. Поглощение. Виды спектров поглощения. Фазовая и групповая скорости света.
Поглощением света называется явление уменьшения энергии световой волны при её распространении в веществе, происходящее вследствие преобразования энергии волны во внутреннюю энергию вещества. Поглощение света может вызвать нагревание вещества, возбуждение и ионизацию атомов или молекул и другие процессы в веществе.
Поглощение света описывается законом Бунгера - Ламберта, согласно
которому, интенсивность I плоской волны монохроматического света
уменьшается
по мере прохождения через поглощающую
среду по
экспонтенциальному
закону:
![]() где
Iо
и I
- значения интенсивности на входе и
выходе из слоя среды толщиной х, а
где
Iо
и I
- значения интенсивности на входе и
выходе из слоя среды толщиной х, а
![]() - натуральный показатель поглощения
среды, который
зависит
от химической природы и состояния
поглощающей среды и от длины
- натуральный показатель поглощения
среды, который
зависит
от химической природы и состояния
поглощающей среды и от длины
волны света.
Виды спектров поглощения: Линейчатый спектр поглощения - характерен для одноатомных газов (или паров). Очень резкие и узкие линии в таких спектрах соответствуют частотам собственных колебаний электронов в атомах. Если плотность газа увеличивать, то взаимодействие атомов между собой приводит к уширению линий поглощения.Спектр поглощения в виде полос поглощения – характерен для поглощения молекул. Колебания атомов (и вращение групп атомов) в молекулах приводят к тому, что образуются широкие полосы поглощения.
Сплошной спектр поглощения – характерен для жидкостей и твердых тел, в которых образуются коллективные возбуждения (например, электроны проводимости в металлах) которые обуславливают поглощение света в широкой области частот (длин волн).
На
рисунке показана зависимость коэффициента
поглощения ![]() от
длины волны λ и зависимость показателя
преломления n от λ в области полосы
поглощения. Внутри полосы поглощения
наблюдается аномальная
дисперсия.
от
длины волны λ и зависимость показателя
преломления n от λ в области полосы
поглощения. Внутри полосы поглощения
наблюдается аномальная
дисперсия.
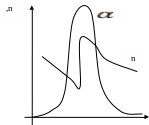 Дисперсия
света - зависимость показателя преломления
вещества n от
Дисперсия
света - зависимость показателя преломления
вещества n от
частоты
v
(длины волны ![]() )
света (или зависимость фазовой скорости
υ
)
света (или зависимость фазовой скорости
υ
световых волн от его частоты v).
Следствием дисперсии является разложение в спектр пучка белого света при
п
А
А

















![]()

![]()
![]()
Рассмотрим
дисперсию света в призме.
Пусть монохроматический луч под углом![]() падает на призму с показателем преломления
n и преломляющим углом А.После двукратного
преломления на левой и правой гранях
призмы луч откланяется на угол
падает на призму с показателем преломления
n и преломляющим углом А.После двукратного
преломления на левой и правой гранях
призмы луч откланяется на угол ![]()
![]() -
угол отклонения лучей призмой тем
больше, чем больше преломляющий угол
призмы.
-
угол отклонения лучей призмой тем
больше, чем больше преломляющий угол
призмы.
В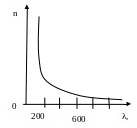 еличина
еличина
![]() называется
дисперсией вещества. Для всех прозрачных
веществ показатель преломления
уменьшается с увеличением длины
волны:
называется
дисперсией вещества. Для всех прозрачных
веществ показатель преломления
уменьшается с увеличением длины
волны:![]() .Такая
дисперсия называется нормальной. Вблизи
линий и полос сильного поглощения ход
кривой n
.Такая
дисперсия называется нормальной. Вблизи
линий и полос сильного поглощения ход
кривой n![]() - кривой дисперсии- обратный:
- кривой дисперсии- обратный:
![]() .
Такая дисперсия называется аномальной.
На
явлении нормальной дисперсии основано
действие призменных спектрографов.
Угол отклонения лучей призмой зависит
от показателя преломления, который в
свою очередь, зависит от длины волны.
Поэтому призма
разлагает белый свет в спектр, отклоняя
красные лучи (длина волны больше) слабее,
чем фиолетовые (длина волны меньше)
.
Такая дисперсия называется аномальной.
На
явлении нормальной дисперсии основано
действие призменных спектрографов.
Угол отклонения лучей призмой зависит
от показателя преломления, который в
свою очередь, зависит от длины волны.
Поэтому призма
разлагает белый свет в спектр, отклоняя
красные лучи (длина волны больше) слабее,
чем фиолетовые (длина волны меньше)

 луч белов. Луч красного света.
луч белов. Луч красного света.

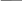



 света
света
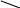 S
S
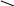

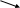 Луч
фиолетового цвета.
Луч
фиолетового цвета.
Фазовая
скорость света - скорость V
распространения синусоидальной
волны.
Она равна скорости перемещения в
пространстве точек поверхности,
соответствующей
любому фиксированному значению фазы
синусоидальной
волны.
Групповая
скорость
U
-это скорость распространения
несинусоидальной волны
и
пригодна для описания переноса энергии
посредством несинусоидальных волн.
Связь между групповой
скоростью
U
и фазовой V
скоростями волн имеют вид
![]() ,
где λ-
длине волны.
,
где λ-
длине волны.
№29 Развитие представлений о природе света. Квантовая природа света. Виды оптических излучений. Источники и приемники света. Некогерентные и когерентные источники света. Квантовые генераторы. Интерференция света.
Исторически почти одновременно были выдвинуты две теории света: корпускулярная теория Ньютона и волновая теория Гюйгенса. Согласно корпускулярной теории светящиеся тела излучают мельчайшие частицы (корпускулы), которые распространяются прямолинейно по всем направлениям. Согласно волновой теории светящиеся тела вызывают в окружающей среде упругие колебания, которые распространяются в среде подобно звуковым волнам. Обе теории продолжительное время сосуществовали. Квантовая механика объединила собой свойства частиц и волн. Фотоны и электроны не являются классическими объектами, они имеют квантовую природу. Волновые и квантовые способы описания света не противоречат, а взаимно дополняют друг друга, так как свет одновременно обладает и волновыми и корпускулярными свойствами.
Виды оптических излучений. Колебания электрических зарядов, входящих в состав вещества, обуславливают электромагнитное излучение, которое сопровождается потерей энергии веществом.
При рассеивании и отражении света формирование вторичных световых волн и продолжительность излучения веществом происходит за время, сравнимое с периодом световых колебаний.
Если излучение продолжается в течение времени, значительно превышающем период световых колебаний, то возможно два типа излучении:1) тепловое излучение 2) люминесценция.
Равновесным состоянием системы тело- излучение является состояние, при котором распределение энергии между телом и излучением остается неизменной для каждой длины волны. Единственным видом излучения, которое может находится в равновесии с излучающим телом, является тепловое излучение – свечение тел обусловленное нагреванием.
Люминесценцией называется неравновесное излучение, избыточное при данной температуре над тепловым излучением тела и имеющее длительность, большую периода световых колебаний.
Источники света. Согласно представлениям классической электродинамики электромагнитные волны возбуждаются электрическими зарядами, движущимися с ускорением. Простейшей излучающей системой является электрический диполь, момент Ре которого изменяется с течением времени. Такой „колеблющийся" диполь называется осциллятором. Источниками света являются атомы, в которых электроны движутся с ускорением вокруг ядра.
Когерентные и некогерентные источники света. Когерентностью называется согласованное протекание во времени и пространстве несколько колебательных или волновых процессов. Когерентными волнами являются волны монохроматические - неограниченные в пространстве волны одной определённой и постоянной частоты.
Реальные источники не дают строго монохроматического света, то волны, излучаемые любыми независимыми источниками света всегда некогерентны. Чтобы было возможно наблюдать интерференцию излучаемых источниками волн, источники должны быть пространственно когерентными.
Пространственная когерентность - когерентность колебаний в один и тот же момент времени, но в разных точках - теряется, если разброс фаз в этих точках достигает π Длина пространственной когерентности (радиус когерентности) r= λ/∆φ где: λ - длина волны, ∆φ - разность фаз.
Квантовые генераторы– электронные устройства для получения и усиления когерентных электромагнитных волн, работа которых основана на явлении вынужденного излучения. Излучение создают связанные электроны, входящие в состав атомов и молекул рабочего вещества.
Вынужденное излучение возникает в результате одновременного, согласованного по частоте и направлению испускания электромагнитных волн огромным количеством атомов или молекул вещества под действием внешнего поля..
Электроны в атомах могут занимать только вполне определенные энергетические уровни Е0, Е1, Е2 …. Уровень Е0, соответствующий наименьшей энергии, называется основным, остальные – возбужденными. Под действием кванта электромагнитного излучения электрон может перейти с одного уровня на другой. Если переход осуществляется с низкого уровня на более высокий, происходит поглощение кванта излучения. Обратный переход сопровождается его испусканием, причем частота и фаза возникшей и первичной волн в точности совпадают. Это излучение называется вынужденным.
Т.о., в результате вынужденного излучения каждый квант, действующий на возбужденный атом удваивается. И если количество возбужденных атомов вещества больше, чем его атомов в основном состоянии, вещество начинает усиливать проходящую сквозь него электромагнитную волну.
Вещество не только может усиливать электромагнитные волны, но одновременно и поглощает их. Величина усиления зависит от соотношения между числом актов вынужденного излучения и величиной потерь. Чем оно больше, тем больше коэффициент усиления. Его можно повысить, если заставить электромагнитную волну проходить активное вещество многократно, увеличивая число излученных квантов. Для этого вещество помещают в полость, ограниченную отражающими стенками – резонатор. Волну вводят в резонатор через отверстие связи в его стенке, и сквозь нее же выводят усиленное излучение, увеличивая тем самым потери. Поэтому коэффициент усиления такого квантового усилителя будет расти при уменьшении отверстия связи.
Квантовые генераторы оптического диапазона называются лазерами. Квантовые усилители, атомные и молекулярные генераторы, работающие в радиодиапазоне, объединяют термином «мазеры», – усиление микроволн при помощи вынужденного излучения.
Интерференция света - сложение в пространстве двух или нескольких когерентных световых волн, при котором в разных его точках получается усиление или ослабления амплитуды результирующей волны.
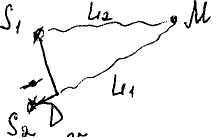
Пусть
в данной точке М две монохроматические
волны
с циклической частотой ω
возбуждают два колебания.
Одна волна прошла в среде с показателем
преломления n1.
путь S1.
с фазовой скоростью υ1,
а
вторая - в среде n2,
путь S2.
с фазовой скоростью υ2
![]() ,
,
![]()
![]()
Интенсивность
результирующей волны (Ι![]() ):Ι
):Ι![]()
Разность фаз δ колебаний, возбуждаемых в точке М, равна:
![]()
![]()
где: L = S • n - оптическая длина пути
Δ=L2-L1=S2n2-S1n1 разность хода волн.
![]() Условие
интерференционного максимума (в
произвольной точке М
Условие
интерференционного максимума (в
произвольной точке М
![]()
если оптическая разность
хода ∆ равна целому числу длин в вакууме (или чётному числу полуволн)
и колебания в точке М, будут происходить в одинаковой фазе.
У![]() словие
интерференционного минимума если
словие
интерференционного минимума если
![]()
оптическая разность хода ∆ равна нечётному числу полуволн и колебания, возбуждаемые в точке М, будут происходить в противофазе. В результате интерференции в точке М будет наблюдаться на орбите интерференционная картина чередования максимумов и минимумов энергии.
№30 Особенности поведения микрообъектов. Тепловое излучение. Корпускулярные свойства света. Импульс фотона. Волновые свойства частиц., волновой вектор. Излучение черного тела, ультрафиолетовая катастрофа. Внешний фотоэффект. Эффект Комптона.
Тепловое излучение совершается за счет энергии теплового движения атомов и молекул вещества (внутренней энергией) и свойственно всем телам при температуре выше 0К. Тепловое излучение равновесно – тело в единицу времени поглощает столько же энергии сколько и излучает.
Количественной
характеристикой теплового излучения
служит спектральная плотность
энергетической светимости (испускательная
способность) тела![]() - мощность излучения с единицы площади
поверхности тела в интервале частот
единичной ширины. (
- мощность излучения с единицы площади
поверхности тела в интервале частот
единичной ширины. (![]() энергия
электромагнитного излучения, испускаемого
за 1 с с площади 1 м2
поверхности тела в интервале частот от
ν до
энергия
электромагнитного излучения, испускаемого
за 1 с с площади 1 м2
поверхности тела в интервале частот от
ν до![]() ). Её единица измерения – Дж на м2.
). Её единица измерения – Дж на м2.
Интегральная
по ν энергетическая светимость
![]()
Способность
тел поглощать падающее на них излучение
характеризуется спектральной
поглощательной способностью![]() , показывающей, какая доля энергии
, показывающей, какая доля энергии
![]() )
приносимой за единицу времени на единицу
площади тела падающими на неё
электромагнитными волнами с частотой
ν до
, поглощается телом.
)
приносимой за единицу времени на единицу
площади тела падающими на неё
электромагнитными волнами с частотой
ν до
, поглощается телом.
Тело
способное поглощать при любой температуре
всё падающее на него излучение любой
частоты называется абсолютно черным
телом. Спектральная поглощательная
способность черного тела для всех частот
и температур тождественно равна единице:
![]() .
.
Закон
Кирхгофа определяет соотношение между
испускательной и поглощательной
способностями тел. Отношение испускательной
и поглощательной способностей тела не
зависит от природы тела и является
универсальной для всех тел функцией
частоты и температуры![]()
Для
черного тела
,
поэтому универсальная функция Кирхгофа
rν,T
есть спектральная плотность энергетической
светимости (испускательная способность)
черного тела.![]() - энергетическая светимость черного
тела , которая зависит только от
температуры. Эту зависимость только
описывает экспериментальный закон
Стефана-Бльцмана: энергетическая
светимость черного тела пропорциональна
четвертой степени термодинамической
температуры:
- энергетическая светимость черного
тела , которая зависит только от
температуры. Эту зависимость только
описывает экспериментальный закон
Стефана-Бльцмана: энергетическая
светимость черного тела пропорциональна
четвертой степени термодинамической
температуры:![]() ,
где
,
где ![]() =5,67·10-8
Вт/
=5,67·10-8
Вт/![]() - постоянная Стефана-Больцмана.
- постоянная Стефана-Больцмана.
Закон
Стефана-Больцмана ничего не говорит о
спектральном составе излучения черного
тела. Положение максимума в спектре его
излучения описывается экспериментальным
законом смещения Вина:  Длина волны λmax,
при которой излучательная способность
Длина волны λmax,
при которой излучательная способность
![]() черного тела максимальна, обратно
пропорциональна его термодинамической
температуре:
черного тела максимальна, обратно
пропорциональна его термодинамической
температуре:
![]() ,где
b=2,9·10-3м·К- постоянная Вина.
,где
b=2,9·10-3м·К- постоянная Вина.
Применяя
к тепловому излучению классический
закон равнораспределения энергии по
степеням свободы Рэлей и Джинс получили
выражение для зависимости испускательной
способности черного тела
от частоты света: ![]() =
=![]() ,
где
,
где ![]() -
средняя энергия осциллятора с собственной
частотой ν.
-
средняя энергия осциллятора с собственной
частотой ν.
Однако
попытка получить закон Стефана-Больцмана
из этой формулы приводит к абсурдному
результату - ![]() неограниченно растет, достигая чрезвычайно
больших значений в ультрафиолете, -
который получил название «ультрафиолетовая
катастрофа»:
неограниченно растет, достигая чрезвычайно
больших значений в ультрафиолете, -
который получил название «ультрафиолетовая
катастрофа»:
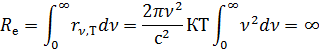
Формула Рэлея-Джинса согласуется с экспериментом только в области малых частот и больших температур.
В нешним
фотоэффектом называется испускание
электронов веществом под действием
электромагнитного излучения. Схема для
исследования внешнего фотоэффекта. Два
электрода катод и анод в вакуумной
трубке подключены к батарее так, что
можно изменять не только значение, но
и знак подаваемого напряжения. Ток,
возникающий при освещении катода
монохроматическим светом (через кварцевое
окошечко) измеряется включенным в цепь
миллиамперметром. Зависимость фототока
І, образуемого потоком электронов,
испускаемых катодом под действием
света, от напряжения U между катодом и
анодом называется вольт-амперной
характеристикой фотоэффекта.
нешним
фотоэффектом называется испускание
электронов веществом под действием
электромагнитного излучения. Схема для
исследования внешнего фотоэффекта. Два
электрода катод и анод в вакуумной
трубке подключены к батарее так, что
можно изменять не только значение, но
и знак подаваемого напряжения. Ток,
возникающий при освещении катода
монохроматическим светом (через кварцевое
окошечко) измеряется включенным в цепь
миллиамперметром. Зависимость фототока
І, образуемого потоком электронов,
испускаемых катодом под действием
света, от напряжения U между катодом и
анодом называется вольт-амперной
характеристикой фотоэффекта.
По мере увеличения U фототок постепенно возрастает пока не на насыщение. Максимальное значение тока Інас – фототок насыщения –
определяется таким значением U, при котором все электроны, испускаемые катодом достигнут анода: Інас=еn, где n – число электронов, испускаемых катодом в 1 с.
При
U=0 фототок не исчезает, поскольку
фотоэлектроны при вылете из катода
обладают некоторой начальной скоростью.
Для того чтобы фототок стал равным нулю,
необходимо приложить задерживающее
напряжение ![]() .
При
.
При ![]() ни один из электронов не может преодолеть
задерживающего поля и достигнуть анода:
ни один из электронов не может преодолеть
задерживающего поля и достигнуть анода:
![]() ,
т.е. измерив задерживающее напряжение
, можно определить максимальное значение
скорости и кинетическую энергию
,
т.е. измерив задерживающее напряжение
, можно определить максимальное значение
скорости и кинетическую энергию ![]() фотоэлектронов.
фотоэлектронов.
Для
объяснения механизма Фотоэффекта
Эйнштейн предположил, что свет частотой
ν не только испускается отдельными
квантами, но и распространяется в
пространстве и поглощается отдельными
порциями, энергия которых ![]() Энергия падающего фотона расходуется
на совершение работы выхода А из металла
и на сообщение вылетевшему фотоэлектрону
кинетической энергии. Уравнение Эйнштейна
для внешнего фотоэффекта:
Энергия падающего фотона расходуется
на совершение работы выхода А из металла
и на сообщение вылетевшему фотоэлектрону
кинетической энергии. Уравнение Эйнштейна
для внешнего фотоэффекта: ![]() .
.
Это
уравнение объясняет зависимость
кинетической энергии фотоэлектронов
от частоты падающего света (2 закон)
Предельная частота ![]() , при котором кинетическая энергия
фотоэлектронов равна нулю, и есть красная
граница фотоэффекта( 3 закон).
, при котором кинетическая энергия
фотоэлектронов равна нулю, и есть красная
граница фотоэффекта( 3 закон).
Используя
соотношения ![]()
![]() ,
,
![]() получаем выражения для энергии массы
и импульса фотона
получаем выражения для энергии массы
и импульса фотона
![]()
![]() ,
,
![]()
Эти соотношения связывают корпускулярные характеристики фотона – массу, импульс и энергию – с волновой – частотой.
К орпускулярные
свойства света отчетливо проявляются
в эффекте Комптона – упругом рассеянии
коротковолнового электромагнитного
излучения (рентгеновского и
орпускулярные
свойства света отчетливо проявляются
в эффекте Комптона – упругом рассеянии
коротковолнового электромагнитного
излучения (рентгеновского и ![]() - излучения) на свободных электронах
вещества, сопровождающееся увеличением
длины волны. Это увеличение
- излучения) на свободных электронах
вещества, сопровождающееся увеличением
длины волны. Это увеличение ![]() не зависит от длины волны λ падающего
излучения и от природы рассеивающего
вещества, а определяется только углом
рассеяния θ:
не зависит от длины волны λ падающего
излучения и от природы рассеивающего
вещества, а определяется только углом
рассеяния θ: ![]() ,
где
,
где ![]() -
длина волны рассеянного излучения,
-
длина волны рассеянного излучения, ![]() - комптоновская длина волны.
- комптоновская длина волны.
Эффект Комптона не может наблюдаться в видимой области спектра, поскольку энергия фотона видимого света сравнима с энергией связи электрона с атомом, при этом даже внешний электрон атома нельзя считать свободным.
№31 Атом Томпсона. Опыты Резерфорда. Планетарная модель строения атома. Гиромагнитное соотношение. Спектр излучения атомарного водорода. Обобщенная формула Бальмера. Модель бора и ее историческая роль, постулаты Бора. Квантование физических характеристик.
 Модель
атома Томпсона. Опыт Резерфорда. Ядерная
модель атома.
Томсон
считал, что атом представляет собой
электронейтральную систему шарообразной
формы радиусом примерно равным 10–10 м.
Положительный заряд атома равномерно
распределен по всему объему шара, а
отрицательно заряженные электроны
находятся внутри него (рисунок).
Для объяснения линейчатых спектров
испускания атомов Томсон пытался
определить расположение электронов в
атоме и рассчитать частоты их колебаний
около положений равновесия. Однако эти
попытки не увенчались успехом. В опытах
Э. Резерфорда было доказано, что
модель Томсона неверна. Резерфорд
предложил применить зондирование атома
с помощью - частиц, которые возникают
при радиоактивном распаде радия и
некоторых других элементов. Резерфорд
использовал α-частицы Этими частицами
Резерфорд бомбардировал атомы тяжелых
элементов (золото, серебро,.). Электроны,
входящие в состав атомов, вследствие
малой массы не могут заметно изменить
траекторию α-частицы. Рассеяние, то есть
изменение направления движения α-частиц,
может вызвать только тяжелая положительно
заряженная часть атома. От радиоактивного
источника, заключенного в свинцовый
контейнер, α-частицы направлялись на
тонкую металлическую фольгу. Рассеянные
частицы попадали на экран, покрытый
слоем кристаллов сульфида цинка,
способных светиться под ударами быстрых
заряженных частиц. Вспышки на экране
наблюдались глазом с помощью микроскопа.
Наблюдения рассеянных α-частиц в опыте
Резерфорда можно было проводить под
различными углами φ к первоначальному
направлению пучка. Было обнаружено, что
большинство α-частиц проходит через
тонкий слой металла, практически не
испытывая отклонения. Однако небольшая
часть частиц отклоняется на значительные
углы, превышающие 30°. Очень редкие
α-частицы испытывали отклонение на
углы, близкие к 180°
Модель
атома Томпсона. Опыт Резерфорда. Ядерная
модель атома.
Томсон
считал, что атом представляет собой
электронейтральную систему шарообразной
формы радиусом примерно равным 10–10 м.
Положительный заряд атома равномерно
распределен по всему объему шара, а
отрицательно заряженные электроны
находятся внутри него (рисунок).
Для объяснения линейчатых спектров
испускания атомов Томсон пытался
определить расположение электронов в
атоме и рассчитать частоты их колебаний
около положений равновесия. Однако эти
попытки не увенчались успехом. В опытах
Э. Резерфорда было доказано, что
модель Томсона неверна. Резерфорд
предложил применить зондирование атома
с помощью - частиц, которые возникают
при радиоактивном распаде радия и
некоторых других элементов. Резерфорд
использовал α-частицы Этими частицами
Резерфорд бомбардировал атомы тяжелых
элементов (золото, серебро,.). Электроны,
входящие в состав атомов, вследствие
малой массы не могут заметно изменить
траекторию α-частицы. Рассеяние, то есть
изменение направления движения α-частиц,
может вызвать только тяжелая положительно
заряженная часть атома. От радиоактивного
источника, заключенного в свинцовый
контейнер, α-частицы направлялись на
тонкую металлическую фольгу. Рассеянные
частицы попадали на экран, покрытый
слоем кристаллов сульфида цинка,
способных светиться под ударами быстрых
заряженных частиц. Вспышки на экране
наблюдались глазом с помощью микроскопа.
Наблюдения рассеянных α-частиц в опыте
Резерфорда можно было проводить под
различными углами φ к первоначальному
направлению пучка. Было обнаружено, что
большинство α-частиц проходит через
тонкий слой металла, практически не
испытывая отклонения. Однако небольшая
часть частиц отклоняется на значительные
углы, превышающие 30°. Очень редкие
α-частицы испытывали отклонение на
углы, близкие к 180°
Этот
результат находился в резком противоречии
с моделью атома Томсона. При таком
распределении положительный заряд не
может создать сильное электрическое
поле, способное отбросить α-частицы
назад. Электрическое поле однородного
заряженного шара максимально на его
поверхности и убывает до нуля по мере
приближения к центру шара. Если бы радиус
шара, в котором сосредоточен весь
положительный заряд атома, уменьшился
в n
раз, то максимальная сила отталкивания,
действующая на α-частицу по закону
Кулона,
возросла бы в n2
раз. Следовательно, при достаточно
большом значении n
α-частицы могли бы испытать рассеяние
на большие углы вплоть до 180°. Эти
соображения привели Резерфорда к выводу,
что атом почти пустой, и весь его
п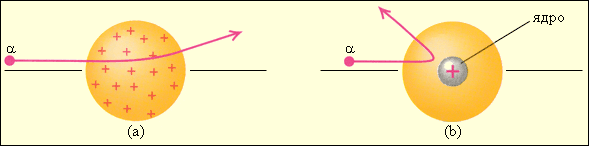 оложительный
заряд сосредоточен в малом объеме. Эту
часть атома Резерфорд назвал атомным
ядром.
Так возникла ядерная
модель
атома.
оложительный
заряд сосредоточен в малом объеме. Эту
часть атома Резерфорд назвал атомным
ядром.
Так возникла ядерная
модель
атома.
Рисунок 9.1.3. Рассеяние α-частицы в атоме Томсона (a) и в атоме Резерфорда (b)
Опираясь на классические представления о движении микрочастиц, Резерфорд предложил планетарную модель атома. Согласно этой модели, в центре атома располагается положительно заряженное ядро, в котором сосредоточен весь положительный заряд почти вся масса атома. Атом в целом нейтрален. Вокруг ядра, подобно планетам, вращаются под действием кулоновских сил со стороны ядра электроны.
Квантовые постулаты Бора .Планетарная модель атома, предложенная Резерфордом, – это попытка применения классических представлений о движении тел к явлениям атомных масштабов. Эта попытка оказалась несостоятельной. Классический атом неустойчив. Электроны, движущиеся по орбите с ускорением, должны неизбежно упасть на ядро, растратив всю энергию на излучение электромагнитных волн. Проанализировав всю совокупность опытных фактов, Бор пришел к выводу, что при описании поведения атомных систем следует отказаться от многих представлений классической физики. Он сформулировал постулаты, которым должна удовлетворять новая теория о строении атомов.
Первый постулат Бора (постулат стационарных состояний) : атомная система может находится только в особых стационарных или квантовых состояниях, каждому из которых соответствует определенная энергия En. В стационарных состояниях атом не излучает. Согласно первому постулату Бора, атом характеризуется системой энергетических уровней, каждый из которых соответствует определенному стационарному состоянию . Механическая энергия электрона, движущегося по замкнутой траектории вокруг положительно заряженного ядра, отрицательна. Поэтому всем стационарным состояниям соответствуют значения энергии En < 0. При En ≥ 0 электрон удаляется от ядра. Величина |E1| называется энергией ионизации. Состояние с энергией E1 называется основным состоянием атома. Второй постулат Бора (правило частот): при переходе атома из одного стационарного состояния с энергией En в другое стационарное состояние с энергией Em излучается или поглощается квант, энергия которого равна разности энергий стационарных состояний:
|
Отсюда
можно выразить частоту излучения:
![]() .Классическая
ядерная модель атома Резерфорда была
дополнена в теории Бора идеей о квантовании
электронных орбит. Поэтому теорию Бора
иногда называют полуклассической.
.Классическая
ядерная модель атома Резерфорда была
дополнена в теории Бора идеей о квантовании
электронных орбит. Поэтому теорию Бора
иногда называют полуклассической.
Атом водорода.
Линейчатые спектры. Простейший
из атомов- атом водорода. Еще в начале
XIX века были открыты дискретные
спектральные линии в излучении атома
водорода в видимой области (линейчатый
спектр).
Впоследствии закономерности, которым
подчиняются длины волн (или частоты)
линейчатого спектра, были хорошо изучены
количественно. Совокупность спектральных
линий атома водорода в видимой части
спектра была названа серией
Бальмера.
Аналогичные серии спектральных линий
были обнаружены в ультрафиолетовой и
инфракрасной частях спектра. Ридберг
получил эмпирическую формулу для частот
спектральных линий:
![]()
Для серии Бальмера m = 2, n = 3, 4, 5, ... . Для ультрафиолетовой серии (серия Лаймана) m = 1, n = 2, 3, 4, ... . Постоянная R в этой формуле называется постоянной Ридберга. Ее численное значение R = 3,29·1015 Гц.
Правило
квантования,
приводящее к правильным, согласующимся
с опытом значениям энергий стационарных
состояний атома водорода, было введено
Бором. Бор предположил, что момент
импульса электрона, вращающегося вокруг
ядра, может принимать только дискретные
значения, кратные постоянной Планка.
Для круговых орбит правило квантования
Бора записывается в виде:
![]()
![]()
Здесь
me
– масса электрона, υ – его скорость, rn
– радиус стационарной круговой орбиты.
Правило квантования Бора позволяет
вычислить радиусы стационарных орбит
электрона в атоме водорода и определить
значения энергий. Скорость электрона,
вращающегося по круговой орбите
некоторого радиуса r
в кулоновском поле ядра определяется
соотношением
![]() где
e
– элементарный заряд, ε0
– электрическая постоянная. Скорость
электрона υ и радиус стационарной орбиты
rn
связаны правилом квантования Бора.
Отсюда следует, что радиусы стационарных
круговых орбит определяются выражением:
где
e
– элементарный заряд, ε0
– электрическая постоянная. Скорость
электрона υ и радиус стационарной орбиты
rn
связаны правилом квантования Бора.
Отсюда следует, что радиусы стационарных
круговых орбит определяются выражением:
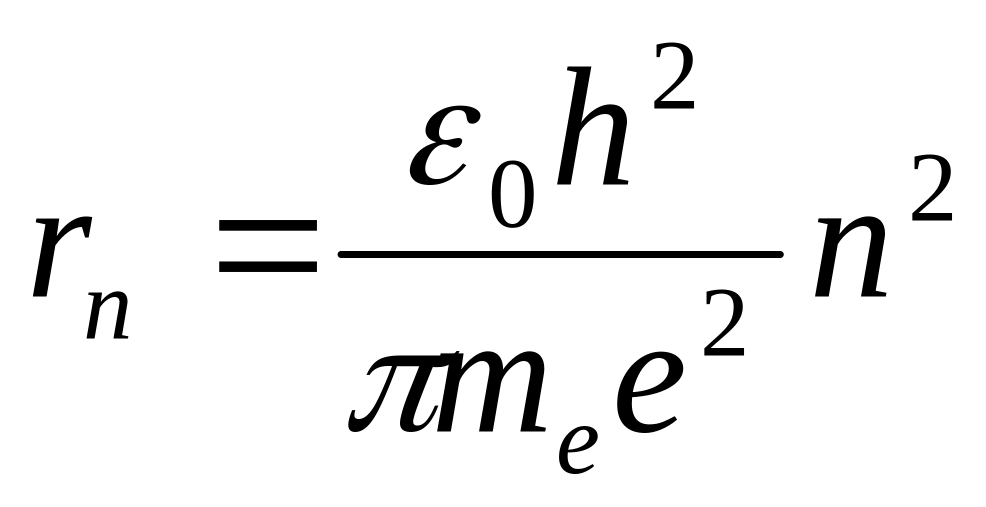 Самой
близкой к ядру орбите соответствует
значение n = 1.
Радиус первой орбиты, который называется
боровским
радиусом,
равен
Самой
близкой к ядру орбите соответствует
значение n = 1.
Радиус первой орбиты, который называется
боровским
радиусом,
равен
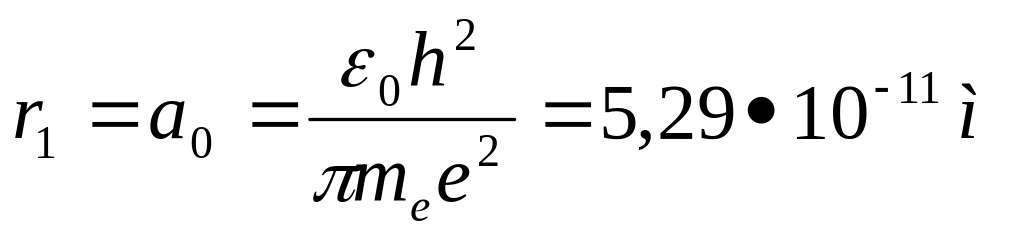 Радиусы
последующих орбит возрастают
пропорционально n2.Полная
механическая энергия E
системы из атомного ядра и электрона,
обращающегося по стационарной круговой
орбите радиусом rn,
равна
Радиусы
последующих орбит возрастают
пропорционально n2.Полная
механическая энергия E
системы из атомного ядра и электрона,
обращающегося по стационарной круговой
орбите радиусом rn,
равна
![]()
Следует
отметить, что Ep < 0,
так как между электроном и ядром действуют
силы притяжения. Подставляя в эту формулу
выражения для υ2
и rn,
получим:
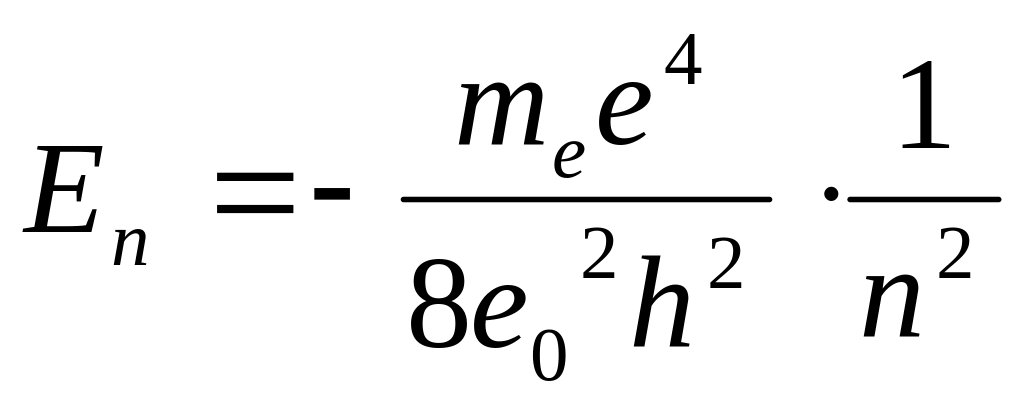 Целое
число n = 1, 2, 3, ...
называется в квантовой физике атома
главным
квантовым числом.
Согласно второму постулату Бора, при
переходе электрона с одной стационарной
орбиты с энергией En
на другую стационарную орбиту с энергией
Em < En
атом испускает квант света, частота νnm
которого равна ΔEnm / h:
Целое
число n = 1, 2, 3, ...
называется в квантовой физике атома
главным
квантовым числом.
Согласно второму постулату Бора, при
переходе электрона с одной стационарной
орбиты с энергией En
на другую стационарную орбиту с энергией
Em < En
атом испускает квант света, частота νnm
которого равна ΔEnm / h:
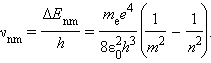
Эта
формула в точности совпадает с эмпирической
формулой Ридберга для спектральных
серий атома водорода, если положить
постоянную R
равной:
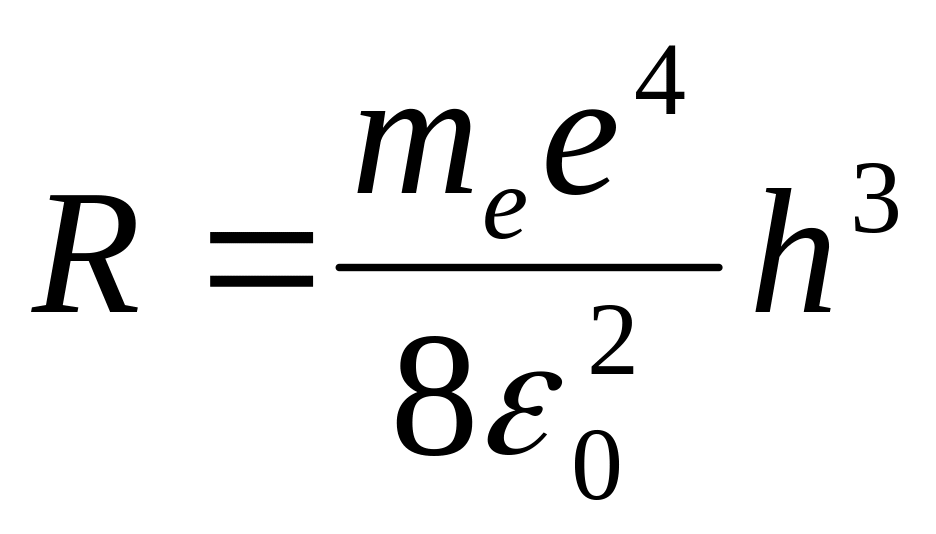
№32 Квантовомеханическая теория атома водорода. Квантовые операторы. Описание состояний атома водорода с помощью квантовых чисел. Кратность вырождения энергии, собственные значения и собственные функции. Спектр излучения атомарного водорода. Правила отбора.
Уравнение Шрёдингера является основным уравнением квантовой механики. Его нельзя вывести из каких-либо известных ранее соотношений, следует рассматривать как исходное основное предположение, справедливость которого доказывается тем, что все вытекающие из него следствия согласуются с опытными фактами.
В
атоме водорода или водородоподобном
ионе потенциальная энергия электрона
равна:
![]()
Уравнение Шрёдингера имеет в этом случае вид:
![]() .
(1.4)
.
(1.4)
Это уравнение имеет однозначные, конечные и непрерывные решения в следующих случаях: 1) при любых положительных значениях Е; 2) при дискретных отрицательных значениях энергии, равных:
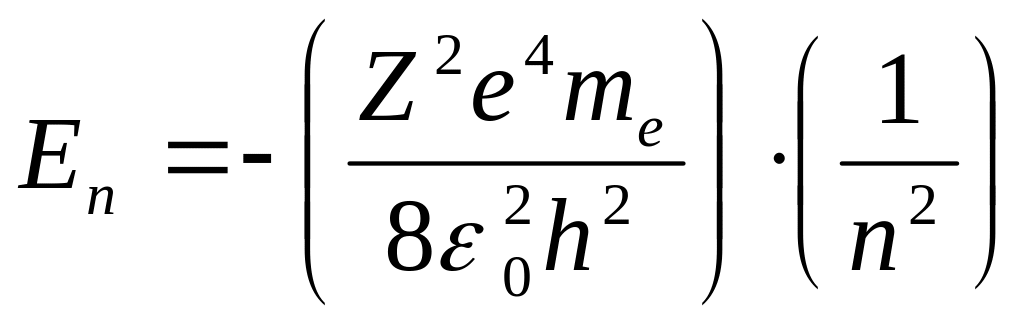 ,
(n=1,
2, 3,…∞). (1.5)
,
(n=1,
2, 3,…∞). (1.5)
Случай Е>0 соответствует электрону, пролетающему вблизи ядра и удаляющемуся вновь на бесконечность. Случай Е<0 соответствует электрону, находящемуся в пределах атома. Значения энергии (En), при которых уравнение Шредингера имеет решение, называются собственными значениями, а соответствующие им волновые функции – собственными функциями. Собственные функции уравнения (1.4) содержат три целочисленных параметра. Один из них совпадает с номером уровня энергии n, два других принято обозначать буквами l и ml. Эти числа называют квантовыми:
n – главное квантовое число; оно определяет энергию (1.5) водородоподобной системы и размеры электронного облака;
l
– орбитальное квантовое число;
оно определяет
форму электронного облака и величину
орбитального момента импульса электрона
(механического момента):![]() ,
,
а
также связанного с ним магнитного
момента
![]() ;
;
ml – магнитное квантовое число; оно определяет проекцию момента импульса на заданное направление в пространстве:
![]() .
(1.8)
.
(1.8)
При заданном n числа l и ml могут принимать следующие значения:
l=0, 1, 2, …, (n–1), то есть всего n значений;
ml=0, ±1, …, ±(l), то есть всего (2.l+1) значений.
Состояния электрона, обладающего различными значениями орбитального квантового числа, в атомной физике принято обозначать и называть следующим образом:
l =0
– s-состояние,
=0
– s-состояние,
l=1 – p-состояние,
l=2 – d-состояние,
l=3 – f-состояние и так далее.
Значение главного квантового числа n указывается перед условным обозначением орбитального l. Таким образом, электрон в состоянии с n=3 и l=1 обозначается символом 3p и т.д.
Вектор
![]() может принимать (2.l+1)
ориентаций в пространстве. На рис.1.1
приведены возможные ориентации вектора
для электронов в p-
и d-состояниях.
может принимать (2.l+1)
ориентаций в пространстве. На рис.1.1
приведены возможные ориентации вектора
для электронов в p-
и d-состояниях.
Таким образом, каждому En, кроме E1, соответствует несколько волновых функций ψnlm, отличающихся значениями квантовых чисел l и ml. Это значит, что атом водорода, имея одну и ту же энергию, может находиться в нескольких различных состояниях. Такие состояния называются вырожденными. Кратность вырождения энергетического уровня с номером n можно рассчитать, исходя из возможных значений n:
![]() .
(1.9)
.
(1.9)
Квантовые
операторы
служат для сопоставления определенной
волновой функции y другой определенной
волновой функции
![]() ':
':
![]() =
=
![]() ,
где
–
оператор. Оператор – это математическое
правило, следуя которому мы можем
преобразовать одну функцию в другую.
Свойства оператора определяются
уравнением
n
=
,
где
–
оператор. Оператор – это математическое
правило, следуя которому мы можем
преобразовать одну функцию в другую.
Свойства оператора определяются
уравнением
n
=![]() n
n, где
n
- решение этого уравнения (собственные
функции уравнения). Числа
n
– собственные
значения оператора. В качестве примера
приведем оператор дифференцирования
n
n, где
n
- решение этого уравнения (собственные
функции уравнения). Числа
n
– собственные
значения оператора. В качестве примера
приведем оператор дифференцирования
![]() .
.
![]() .
.
![]()
В начале XIX века были открыты дискретные спектральные линии в излучении атома водорода в видимой области (линейчатый спектр). Впоследствии закономерности, которым подчиняются длины волн (или частоты) линейчатого спектра, были хорошо изучены количественно. Совокупность спектральных линий атома водорода в видимой части спектра была названа серией Бальмера. Аналогичные серии спектральных линий были обнаружены в ультрафиолетовой и инфракрасной частях спектра. Ридберг получил эмпирическую формулу для частот спектральных линий:
Для серии Бальмера m = 2, n = 3, 4, 5, ... . Для ультрафиолетовой серии (серия Лаймана) m = 1, n = 2, 3, 4, ... . Постоянная R в этой формуле называется постоянной Ридберга. Ее численное значение R = 3,29·1015 Гц.
Испускание и поглощение света происходит при переходе электрона с одного уровня на другой. В квантовой механике доказывается, что для орбитального квантового числа имеется правило отбора
![]() .
(1.13)
.
(1.13)
Это означает, что возможны только такие переходы, при которых l изменяется на единицу. Правило обусловлено тем, что фотон обладает собственным моментом импульса (спином). При испускании фотон уносит из атома этот момент, а при поглощении привносит. Разрешенными являются переходы лишь между s- и р-состояниями, между р- и d-состояниями и т. д.. При этом главное квантовое число п может изменяться на любое целое число. С точки зрения квантовой теории правила отбора связаны с вероятностью перехода из одного квантового состояния в другое.
№ 33. Состояние электрона в многоэлектронном атоме. Электронные слои, электронные оболочки. Количество электронов в слое. Принципы построения многоэлектронного атома. Запись конфигурации атома. Полная энергия, спектр излучения. Периодическая система элементов Д.И. Менделеева.
Состояние каждого электрона в атоме характеризуется четырьмя квантовыми числами:
– главным n (n=1, 2, … ∞),
– орбитальным l (l=0, 1, 2, … n–1),
– магнитным ml (ml=0, 1, 2, … l),
– спиновым ms (ms=1/2).
Данному n соответствуют n2 состояний, отличающихся значениями l и ml. В атоме водорода энергия электрона зависит от n и слабо – от ms и не зависит от l и ml. Каждый уровень энергии является вырожденным, причём кратность вырождения равна
В
многоэлектронных атомах состояние
каждого электрона определяется теми
же квантовыми числами, что и в атоме
водорода. Влияние на данный электрон
остальных электронов проявляется в
том, что поле, в котором движется электрон,
перестаёт быть кулоновским ( то есть
изменяющимся по закону обратных
квадратов:
![]() ~
~![]() ).
Это обусловливает зависимость энергии
электрона также и от орбитального
квантового числа l
(снимается вырождение по квантовому
числу l).
Энергия состояния зависит в основном
от чисел n
и l.
Распределение электронов в атоме по
уровням энергии осуществляется в
соответствии с принципами:
).
Это обусловливает зависимость энергии
электрона также и от орбитального
квантового числа l
(снимается вырождение по квантовому
числу l).
Энергия состояния зависит в основном
от чисел n
и l.
Распределение электронов в атоме по
уровням энергии осуществляется в
соответствии с принципами:
1. Принцип Паули. В одном атоме не может быть двух и более электронов, находящихся в одинаковом стационарном состоянии, то есть с одинаковым набором всех четырёх квантовых чисел.
2. Принцип минимума энергии. В первую очередь заполняются уровни с минимальной энергией, то есть с наименьшими квантовыми числами n, l, ml, ms.
В нормальном (невозбуждённом) состоянии атома электроны располагаются на самых низких доступных для них энергетических уровнях. Совокупность электронов, имеющих одинаковые n и l, образуют оболочку. Данному значению п соответствует 2п2 состояний, отличающихся друг от друга значениями квантовых чисел ℓ, mℓ, ms Совокупность оболочек с одинаковым n образуют слой. Подразделение возможных состояний в атоме на оболочки и слои показано в табл.1. . Распределение электронов по состояниям называют электронной конфигурацией. Их обозначают символически, например, так: ls2 2s2 2p6 3s. Это означает, что в атоме имеются два ls-электрона, два 2s2-электрона, шесть 2р-электронов и один 3s -электрон.
В атоме водорода в основном состоянии имеется один электрон (1s). Если заряд ядра увеличить на единицу и добавить один электрон, получится атом гелия. Оба электрона в атоме гелия в основном состоянии находятся в K-слое. Электронная конфигурация записывается как 1s2, где цифра означает квантовое число п, т. е. принадлежность к соответствующей оболочке (К, L, М, ...).. На атоме гелия заканчивается заполнение K-слоя. Третий электрон атома лития может занять лишь уровень n=2; электронная конфигурация 1s22s. Третий электрон лития, занимая более высокий энергетический уровень, чем остальные два электрона, оказывается слабее, чем они, связанным с ядром атома. В результате он определяет оптические и химические свойства атома.
У четвертого элемента полностью заполняется оболочка 2s. У последующих шести элементов заполняется оболочка 2p. Неон имеет полностью заполненные слои K (двумя электронами) и L (восемью электронами), образующие устойчивую систему, подобную системе гелия, чем обуславливаются специфические свойства инертных газов.
Табл.1
Слой |
n |
l |
ml |
ms |
Обо- лочка |
Максимальное число электронов в оболочке
|
Максимальное число электронов в слое 2 n2 |
Элемент, число электронов z |
K |
1 |
0 |
0 |
|
1s |
2 |
2 |
H (1), He (2) |
L |
2 |
0 |
0 |
|
2s |
2 |
8 |
Li (3), Be (4) |
1 |
0 ±1 |
|
2p |
6 |
B (5), … Ne (10) |
|||
M |
3 |
0 |
0 |
|
3s |
2 |
18 |
Na (11) Mg (12) |
1 |
0 ±1 |
|
3p |
6 |
Al (13), … Ar (18) |
|||
2 |
0 ±1 ±2 |
|
3d |
10 |
Sc (21), … Ni (28) |
|||
N |
4 |
0 |
0 |
|
4s |
2 |
32 |
K (19), Ca (20) |
… |
… |
|||||||
Молекулярные спектры. Молекула – это наименьшая частица вещества, состоящая из одинаковых или различных атомов, соединенных между собой химическими связями. И являющаяся носителем его основных химических свойств. Химические связи обусловлены взаимодействием внешних электронов атомов. Наиболее часто встречаются два типа связи:
Ионная связь осуществляется кулоновским притяжением атомов при переходе электрона от одного атома к другому
Ковалентная связь осуществляется при обобществлении валентных электронов двумя соседними атомами. Наглядно можно представить себе, что электрон каждого атома молекулы проводит некоторое время у ядра другого атома. Такое квантовое взаимодействие называется обменным взаимодействием. Молекула является квантовой системой; она описывается уравнением Шредингера, учитывающим движение электронов в молекуле, колебания атомов в молекуле, вращение молекулы. Энергию изолированной молекулы можно представить в виде суммы:
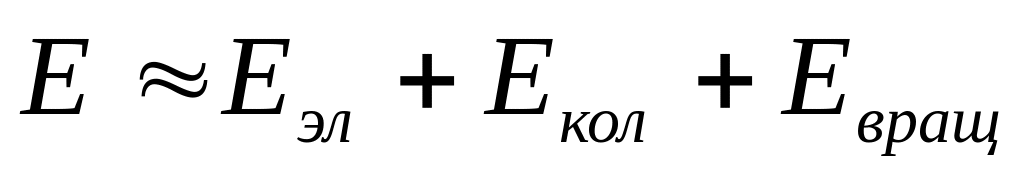 где
где
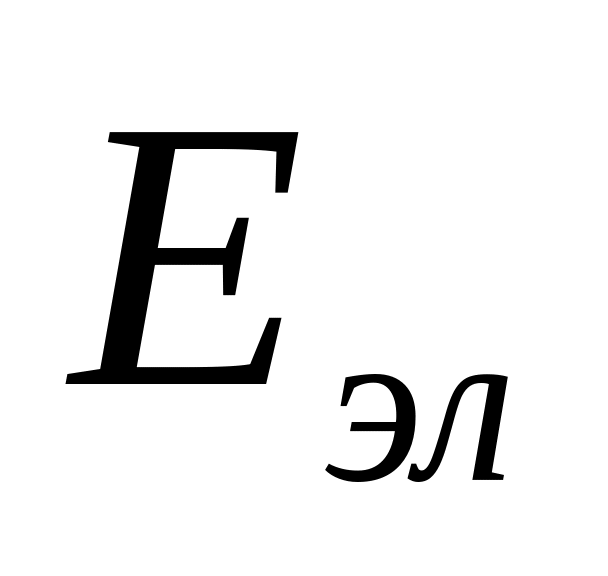 -
энергия движения электронов относительно
ядер,
-
энергия движения электронов относительно
ядер,
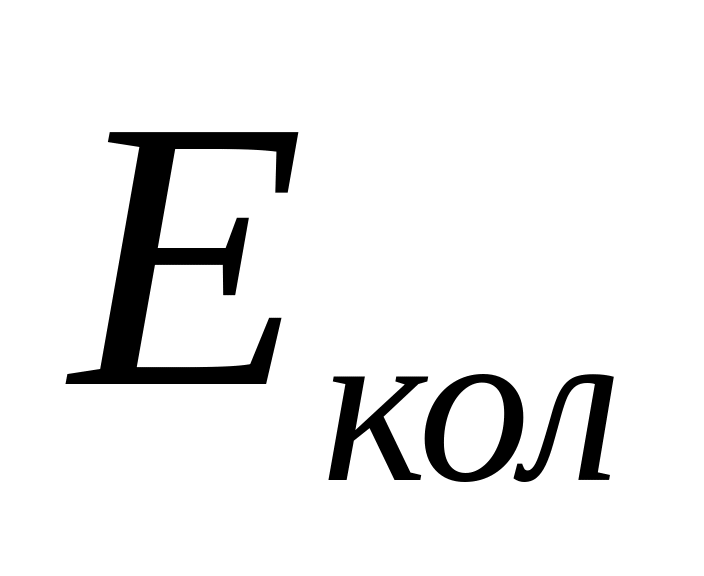 -
энергия колебаний ядер,
-
энергия колебаний ядер,
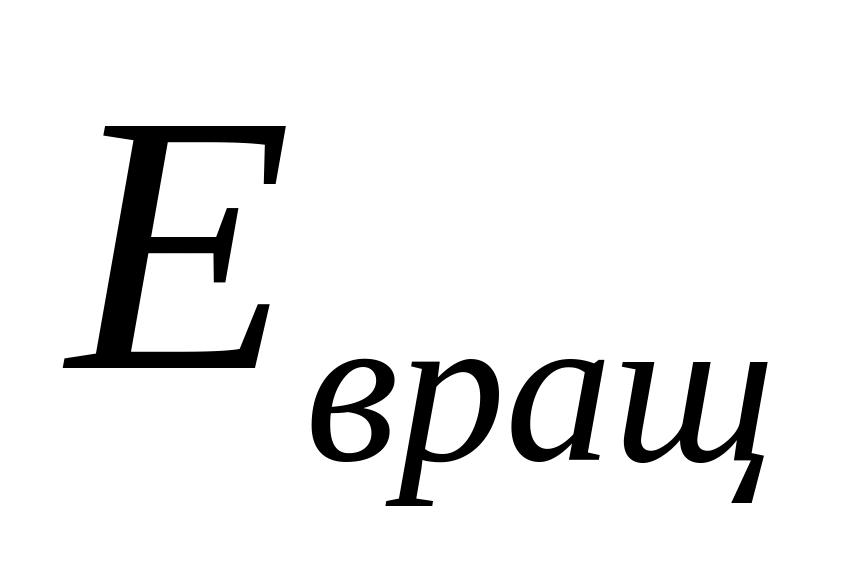 -
энергия вращения ядер. Соотношение
между ними:
-
энергия вращения ядер. Соотношение
между ними:
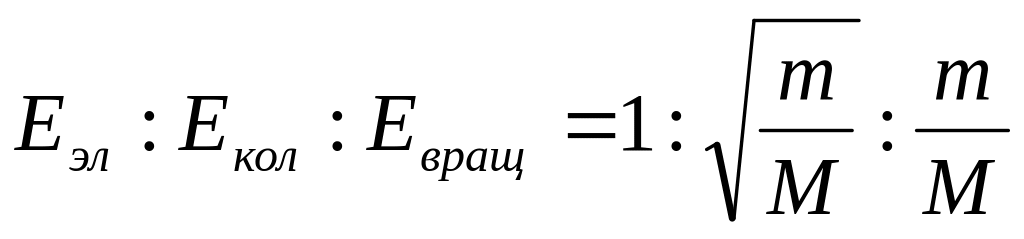 где m- масса электрона, М- величина,
имеющая порядок массы ядер атомов в
молекуле. Поэтому:
где m- масса электрона, М- величина,
имеющая порядок массы ядер атомов в
молекуле. Поэтому:
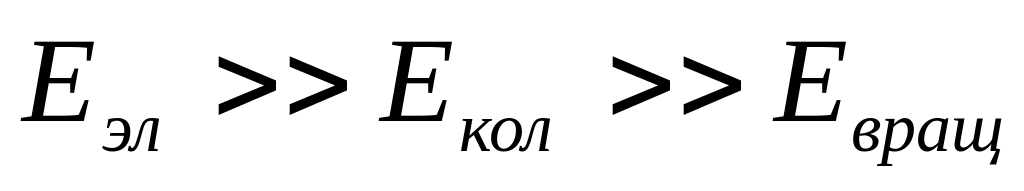 .
Каждая из энергий квантуется и
определяется квантовыми числами.
Колебательная
энергия,
при небольших значениях колебательного
квантового числа
.
Каждая из энергий квантуется и
определяется квантовыми числами.
Колебательная
энергия,
при небольших значениях колебательного
квантового числа
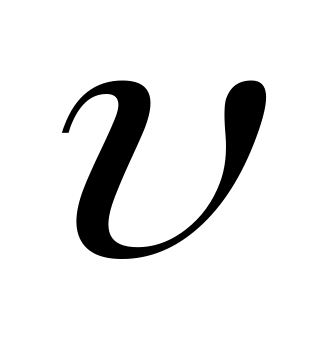 ,
определяется формулой для энергии
гармонического осциллятора:
,
определяется формулой для энергии
гармонического осциллятора:

 При
этом правило отбора для колебательного
квантового числа:
При
этом правило отбора для колебательного
квантового числа:
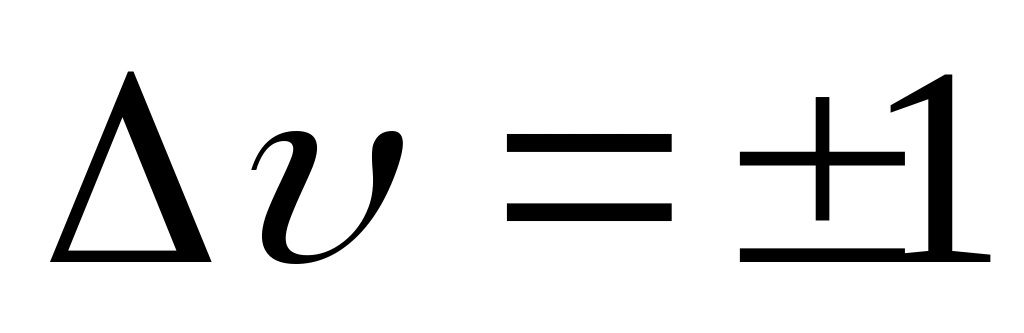 .
Вращательная
энергия
молекулы, вращающейся с угловой скоростью
.
Вращательная
энергия
молекулы, вращающейся с угловой скоростью
 ,
и имеющей момент инерции I относительно
оси, проходящей через центр ее инерции,
равна:
,
и имеющей момент инерции I относительно
оси, проходящей через центр ее инерции,
равна:
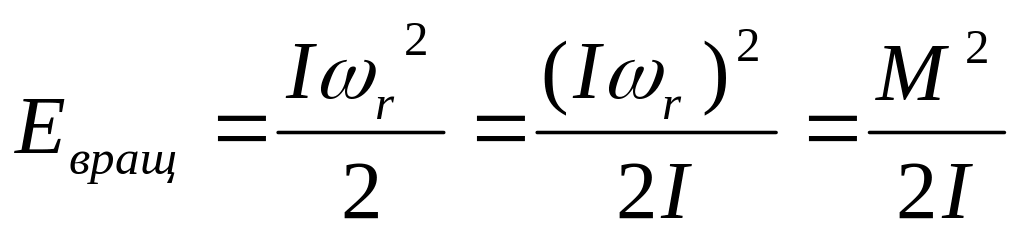 где
где
 -
момент импульса молекулы.Момент импульса
квантуется по закону:
-
момент импульса молекулы.Момент импульса
квантуется по закону:
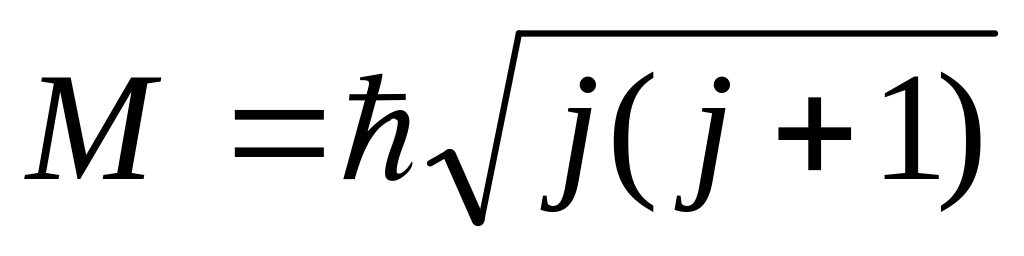
 где j
– вращательное квантовое число.
Следовательно, вращательная энергия
молекулы может иметь только квантованные
значения:
где j
– вращательное квантовое число.
Следовательно, вращательная энергия
молекулы может иметь только квантованные
значения:
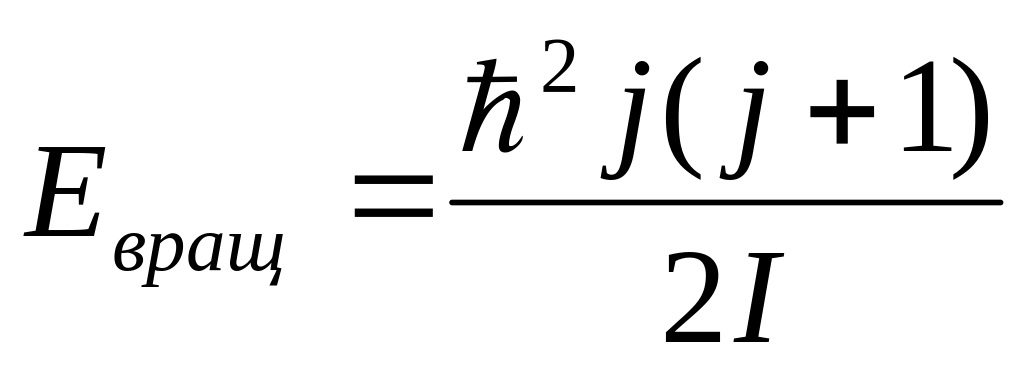 .
Периодическая
система элементов Д.И.Менделеева:
Менделеев
открыл периодический закон изменения
химических и физических свойств
элементов в зависимости от их атомных
масс. Если расположить хим.элементы в
порядке возрастания их атомных масс
то через правильные промежутки,
называемые периодами, элементы
оказавшиеся в одном вертикальном ряду
обнаруживают сходные физико-химические
свойства. Теория периодической системы
основывается на следующих положениях:1)
порядковый номер хим.элемента равен
общему числу электронов в атоме данного
элемента; 2) состояние электронов в
атоме определяется набором их квантовых
чисел
.
Периодическая
система элементов Д.И.Менделеева:
Менделеев
открыл периодический закон изменения
химических и физических свойств
элементов в зависимости от их атомных
масс. Если расположить хим.элементы в
порядке возрастания их атомных масс
то через правильные промежутки,
называемые периодами, элементы
оказавшиеся в одном вертикальном ряду
обнаруживают сходные физико-химические
свойства. Теория периодической системы
основывается на следующих положениях:1)
порядковый номер хим.элемента равен
общему числу электронов в атоме данного
элемента; 2) состояние электронов в
атоме определяется набором их квантовых
чисел
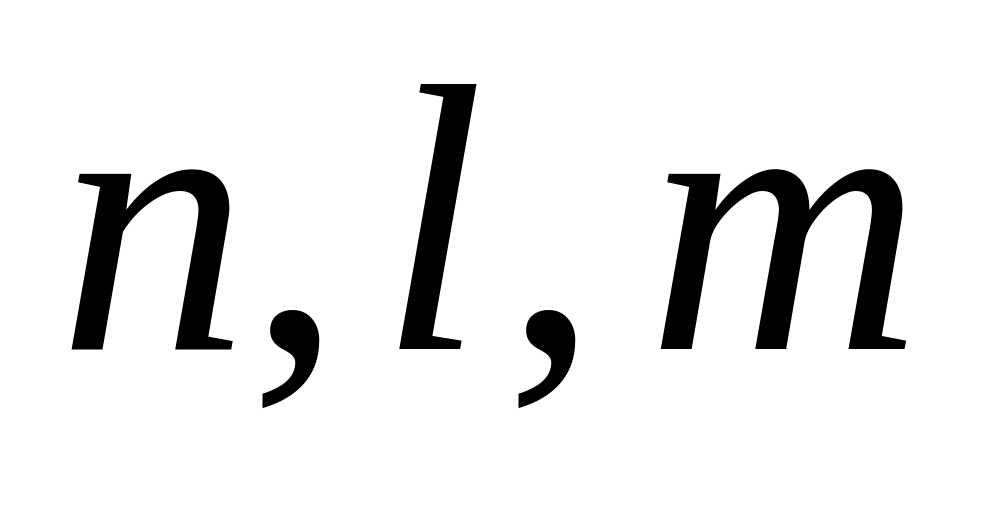 и
и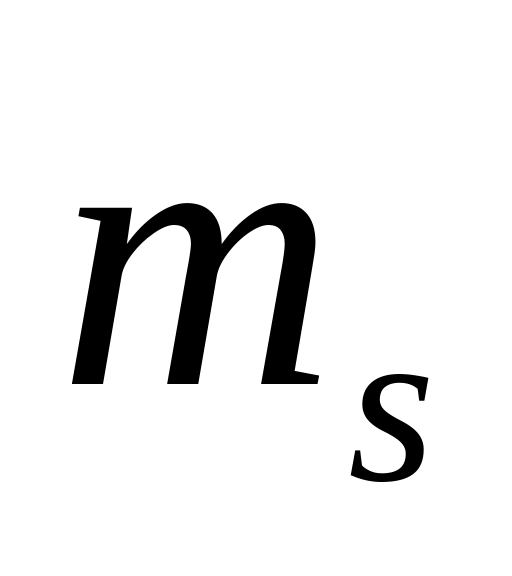 .Распределение
электронов в атоме по энергетическим
состояниям должно удовлетворять
принципу минимума энергии атома. 3)
заполнение электронами энергетических
состояний в атоме должно происходить
в соответствии с принципом Паули.
.Распределение
электронов в атоме по энергетическим
состояниям должно удовлетворять
принципу минимума энергии атома. 3)
заполнение электронами энергетических
состояний в атоме должно происходить
в соответствии с принципом Паули.
№34 Волновые свойства частиц. Волна де-Бройля. Волновая функция, уравнение плоской волны. Волновой пакет, фазовая и групповая скорость. Соотношение неопределенностей на примере дифракции электрона на щели. Вероятностный характер описания поведения микрочастиц. Квадрат волновой функции.
Корпускулярно-волновой
дуализм свойств вещества. Квантовая
механика основывается на предположении
де Бройля о том, что электроны и любые
другие частицы материи наряду с
корпускулярными обладают также волновыми
свойствами. Каждому объекту присущи
как корпускулярные характеристики –
энергия Е и импульс р, так и волновые
характеристики – частота
![]() и длина волны
.
Соотношение между корпускулярными и
волновыми характеристиками частиц
такие же как для фотонов:
и длина волны
.
Соотношение между корпускулярными и
волновыми характеристиками частиц
такие же как для фотонов:
![]() и
и
![]() .
Т. о., любой частице, обладающей импульсом
сопоставляется волновой процесс с
длиной волны, определяемой по формуле
де Бройля:
.
Т. о., любой частице, обладающей импульсом
сопоставляется волновой процесс с
длиной волны, определяемой по формуле
де Бройля:
![]() .
Гипотеза де Бройля была подтверждена
экспериментально в опытах по дифракции
электронов на монокристаллах металлов
– естественных дифракционных решетках
– и на металлических пленках. Даже в
случае чрезвычайно слабых пучков, когда
каждый электрон проходил препятствие
независимо от других электронов пучка,
формировалась дифракционная картина
как в проходящем, так и в отраженном
пучке электронов. Полная энергия частицы
определяется частотой волн де Бройля
с помощью соотношения
.
Гипотеза де Бройля была подтверждена
экспериментально в опытах по дифракции
электронов на монокристаллах металлов
– естественных дифракционных решетках
– и на металлических пленках. Даже в
случае чрезвычайно слабых пучков, когда
каждый электрон проходил препятствие
независимо от других электронов пучка,
формировалась дифракционная картина
как в проходящем, так и в отраженном
пучке электронов. Полная энергия частицы
определяется частотой волн де Бройля
с помощью соотношения
![]() .
Таким образом, корпускулярно-волновой
дуализм – универсальное свойство
материи..
.
Таким образом, корпускулярно-волновой
дуализм – универсальное свойство
материи..
Некоторые
свойства волн де Бройля: рассмотрим
свободно движущуюся со скоростью
частицу массой
.
Фазовая
скорость
волн де
Бройля:
![]() т.е. фазовая скорость волн де Бройля
больше скорости света в вакууме (т.к.
т.е. фазовая скорость волн де Бройля
больше скорости света в вакууме (т.к.
![]() ).
Использованы соотношения:
).
Использованы соотношения:
![]() ,
,
![]() ,
,
![]() -
волновое число. Групповая
скорость
волн де
Бройля:
-
волновое число. Групповая
скорость
волн де
Бройля:
![]() .
Для свободной частицы
.
Для свободной частицы
![]() ,
поэтому
,
поэтому
![]() .
Групповая скорость волн де Бройля равна
скорости частицы. Иными словами, волны
де Бройля перемещаются вместе с частицей.
Для фотона:
.
Групповая скорость волн де Бройля равна
скорости частицы. Иными словами, волны
де Бройля перемещаются вместе с частицей.
Для фотона:
![]() и
и
![]() .
.
Соотношение
неопределенностей Гейзенберга:
микрочастица
не может иметь одновременно определенную
координату
![]() и
определенную соответствующую проекцию
импульса
и
определенную соответствующую проекцию
импульса
![]() ,
причем неопределенности этих величин
удовлетворяют соотношениям
,
причем неопределенности этих величин
удовлетворяют соотношениям
![]() ,
,
![]() ,
,
![]() т.е. произведение неопределенностей
координаты и соответствующей ей проекции
импульса не может быть меньше величины
п
т.е. произведение неопределенностей
координаты и соответствующей ей проекции
импульса не может быть меньше величины
п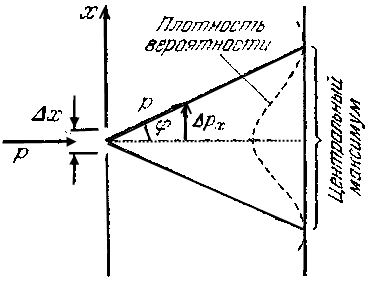 орядка
орядка
![]() .
Соотношение неопределенностей проявляется
в дифракции частиц. Пусть поток частиц
движется вдоль оси
.
Соотношение неопределенностей проявляется
в дифракции частиц. Пусть поток частиц
движется вдоль оси
![]() с
импульсом
с
импульсом
![]() .
До прохождения частицы через щель
составляющая ее импульса
.
До прохождения частицы через щель
составляющая ее импульса
![]() ,
так что
,
так что
![]() ,
а координата
,
а координата
![]() является совершенно неопределенной. В
момент прохождения частицы через щель
неопределенность координаты
частицы становится равной ширине щели
является совершенно неопределенной. В
момент прохождения частицы через щель
неопределенность координаты
частицы становится равной ширине щели
![]() .
Вследствие дифракции частицы будут
двигаться в пределах угла
.
Вследствие дифракции частицы будут
двигаться в пределах угла
![]() ,
где
-
угол, соответствующий первому
дифракционному минимуму. Т.о.
неопределенность в значении составляющей
вдоль оси
:
,
где
-
угол, соответствующий первому
дифракционному минимуму. Т.о.
неопределенность в значении составляющей
вдоль оси
:
![]() .
С другой стороны,
.
С другой стороны,
![]() - условие первого дифракционного
минимума. Следовательно
- условие первого дифракционного
минимума. Следовательно
![]() .
Поскольку часть частиц попадает за
пределы первого дифракционного максимума,
то получаем выражение
,
т.е. соотношение неопределенностей.
Соотношение
неопределенностей –
квантовое ограничение применимости
классической механики к микрообъектам.
Для микрочастицы не существует состояний,
в которых ее координаты и соответствующие
им проекции импульса имели бы одновременно
точные значения. Для неопределенности
энергии
.
Поскольку часть частиц попадает за
пределы первого дифракционного максимума,
то получаем выражение
,
т.е. соотношение неопределенностей.
Соотношение
неопределенностей –
квантовое ограничение применимости
классической механики к микрообъектам.
Для микрочастицы не существует состояний,
в которых ее координаты и соответствующие
им проекции импульса имели бы одновременно
точные значения. Для неопределенности
энергии
![]() некоторого
состояния системы и промежутка времени
некоторого
состояния системы и промежутка времени
![]() ,
в течение которого это состояние
существует, также выполняется соотношение
неопределенностей
,
в течение которого это состояние
существует, также выполняется соотношение
неопределенностей
![]() .
Следовательно система имеющая среднее
время жизни
,
не может быть охарактеризована
определенным значением энергии.
.
Следовательно система имеющая среднее
время жизни
,
не может быть охарактеризована
определенным значением энергии.
Волновая
функция и ее свойства.
Для описания поведения квантовых систем
вводится волновая
функция
(пси-функция)
![]() .
Она определяется таким образом, чтобы
вероятность
.
Она определяется таким образом, чтобы
вероятность
![]() того что частица находится в элементе
объема
того что частица находится в элементе
объема
![]() была
равна:
была
равна:
![]() .
Физический смысл имеет не сама функция
.
Физический смысл имеет не сама функция
![]() ,
а квадрат ее модуля
,
а квадрат ее модуля
![]() ,
которым задается интенсивность волн
де Бройля (здесь
,
которым задается интенсивность волн
де Бройля (здесь
![]() -
функция, комплексно сопряженная с
).
Величина
-
функция, комплексно сопряженная с
).
Величина
![]() имеет смысл плотности вероятности
имеет смысл плотности вероятности
![]() ,
а сама волновая функция
имеет смысл амплитуды вероятностей.
,
а сама волновая функция
имеет смысл амплитуды вероятностей.
![]()
![]() .
Условие нормировки вероятностей
получается из того, что вероятность
существования частицы где-либо в
пространстве равна единице (интеграл
вычисляется по всему бесконечному
пространству). Волновая функция,
характеризующая вероятность обнаружения
действия микрочастицы в элементе объема
должна быть 1) конечной (вероятность не
может быть больше единицы), 2) однозначной
(вероятность не может быть неоднозначной
величиной) и 3) непрерывной (вероятность
не может изменяться скачком). Волновая
функция позволяет вычислить средние
значения физических величин, характеризующих
данный микрообъект. Например, среднее
расстояние
.
Условие нормировки вероятностей
получается из того, что вероятность
существования частицы где-либо в
пространстве равна единице (интеграл
вычисляется по всему бесконечному
пространству). Волновая функция,
характеризующая вероятность обнаружения
действия микрочастицы в элементе объема
должна быть 1) конечной (вероятность не
может быть больше единицы), 2) однозначной
(вероятность не может быть неоднозначной
величиной) и 3) непрерывной (вероятность
не может изменяться скачком). Волновая
функция позволяет вычислить средние
значения физических величин, характеризующих
данный микрообъект. Например, среднее
расстояние
![]() имеет вид:
имеет вид:
![]() .
Волновая функция удовлетворяет принципу
суперпозиции: если система может
находиться в различных состояниях,
описываемых волновыми функциями
.
Волновая функция удовлетворяет принципу
суперпозиции: если система может
находиться в различных состояниях,
описываемых волновыми функциями
![]() то она также может находиться в состоянии,
описываемом линейной комбинацией этих
функций (где
то она также может находиться в состоянии,
описываемом линейной комбинацией этих
функций (где
![]() произвольные,
вообще говоря, комплексные числа)
произвольные,
вообще говоря, комплексные числа)
![]() .
.
№ 35 Уравнение Шрёдингера. Операторы импульса, энергии. Принцип причинности в квантовой механике. Принцип наименьшего действия. Классическая механика как предельный случай квантовой. Принцип соответствия. Стационарное уравнение Шредингера и свойства стационарных состояний.
Общее
уравнение Шредингера. Основное
уравнение нерелятивистской квантовой
механики имеет вид
![]()
![]() где
где
![]() ,
-масса
частицы,
-
оператор Лапласа,
,
-масса
частицы,
-
оператор Лапласа,
![]() -
мнимая единица,
-
мнимая единица,
![]() -
потенциальная функция частицы в силовом
поле, в котором она движется,
-
потенциальная функция частицы в силовом
поле, в котором она движется,
![]() -искомая
волновая функция частицы. Уравнение
дополняется условиями, накладываемыми
на волновую функцию: (1) волновая функция
должна быть конечной, однозначной и
непрерывной; (2) производные
-искомая
волновая функция частицы. Уравнение
дополняется условиями, накладываемыми
на волновую функцию: (1) волновая функция
должна быть конечной, однозначной и
непрерывной; (2) производные
![]() должны быть непрерывны; (3) функция
должны быть непрерывны; (3) функция
![]() должна быть интегрируемая; это условие
в простейших случаях сводится к условию
нормировки вероятностей.
должна быть интегрируемая; это условие
в простейших случаях сводится к условию
нормировки вероятностей.
Уравнение
Шредингера для стационарных состояний
В уравнении
Шредингера для стационарных состояний
исключена зависимость
![]() от
времени и, поэтому, значения этих
состояний являются фиксированными (не
изменяются со временем). В этом случае
силовое поле, в котором движется частица,
стационарно, т.е. функция
от
времени и, поэтому, значения этих
состояний являются фиксированными (не
изменяются со временем). В этом случае
силовое поле, в котором движется частица,
стационарно, т.е. функция
![]() не зависит явно от времени и имеет смысл
потенциальной энергии. Решение уравнения
может быть представлено в виде произведения
двух функций – функции только координат
и функции только времени:
не зависит явно от времени и имеет смысл
потенциальной энергии. Решение уравнения
может быть представлено в виде произведения
двух функций – функции только координат
и функции только времени:
![]() где
где
![]() -
полная энергия частицы.
-
полная энергия частицы.
![]() или
или
![]() -уравнение
Шредингера для стационарных состояний.
Физический
смысл имеют только регулярные волновые
функции - конечные, однозначные и
непрерывные вместе со своими первыми
производными. Эти условия выполняются
только при определенном наборе
.
Эти значения энергии называются
собственными. Решения, которые
соответствуют собственным значениям
энергии, называются собственными
функциями. Собственные значения
могут образовывать как непрерывный,
так и дискретный ряд. В первом случае
говорят о непрерывном (или сплошном)
спектре, во втором – о дискретном
спектре.
-уравнение
Шредингера для стационарных состояний.
Физический
смысл имеют только регулярные волновые
функции - конечные, однозначные и
непрерывные вместе со своими первыми
производными. Эти условия выполняются
только при определенном наборе
.
Эти значения энергии называются
собственными. Решения, которые
соответствуют собственным значениям
энергии, называются собственными
функциями. Собственные значения
могут образовывать как непрерывный,
так и дискретный ряд. В первом случае
говорят о непрерывном (или сплошном)
спектре, во втором – о дискретном
спектре.
Оператор
импульса.
Оператором
называют
символическое обозначение математической
операции, которую необходимо совершить
с интересующей нас функцией. Операторы
принято обозначать буквами со «шляпкой».
С помощью
операций дифференцирования по координатам
определим операторы проекций импульса,
записав эти определения в символической
операторной форме как :
![]() ,
,
![]() ,
,![]()
Все
три формулы в можно объединить в одну,
введя векторный оператор импульса
![]() ,который
запишется как:
,который
запишется как:
![]() .
Здесь
.
Здесь
![]() . Используя соотношение классической
механики
. Используя соотношение классической
механики
![]() определим
оператор квадрата импульса как
определим
оператор квадрата импульса как
![]()
Используя
символ оператора Лапласа, запишем
![]() .
.
Операторы
энергий.
Классическая формула связи кинетической
энергии частицы с квадратом ее импульса
![]() позволяет записать аналогичное
соотношение между соответствующими
операторами, поэтому
позволяет записать аналогичное
соотношение между соответствующими
операторами, поэтому
![]() . Если
частица движется в стационарном силовом
поле, и ее потенциальная энергия
. Если
частица движется в стационарном силовом
поле, и ее потенциальная энергия![]() определена в любой точке пространства,
то оператор потенциальной энергии
определена в любой точке пространства,
то оператор потенциальной энергии
![]() определяется
как оператор умножения на функцию
определяется
как оператор умножения на функцию![]() ,
то есть
,
то есть
![]() или
или
![]() .
Т. к. полная энергия частицы в классической
механике есть сумма кинетической и
потенциальной энергий, то в квантовой
механике оператор полной энергии
.
Т. к. полная энергия частицы в классической
механике есть сумма кинетической и
потенциальной энергий, то в квантовой
механике оператор полной энергии
![]() определяется
как сумма операторов кинетической и
потенциальной энергий:
определяется
как сумма операторов кинетической и
потенциальной энергий:
![]() .
.
Раскрывая
выражение для оператора квадрата
импульса, запишем оператор полной
энергии
![]()
В квантовой механике оператор полной энергии называют оператором функции Гамильтона или просто гамильтонианом.
Принцип причинности: состояние микросистемы в начальный момент времени и закон действия физических полей на микрочастицу в этот момент полностью определяют ее состояние в последующие моменты времени.
Принцип наименьшего действия: из всех возможных движений механической системы практически реализуется только такое, для которого действие по Гамельтону имеет минимальное значение.
