2. Магнитное поле в центре кругового тока.

На расстоянии r от центра витка вдоль оси витка магнитное поле будет .

Энергия магнитного поля. Вокруг проводника с током всегда существует магнитное поле. Магнитное поле всегда появляется и исчезает с появлением и исчезновением тока. Энергия магнитного поля равна работе, которую затрачивает ток на создание магнитного поля.

Пусть имеется контур индуктивностью L с током I. Магнитный поток Ф= LI, а dФ= LdI. Работа dА=I dФ=LIdI, тогда работа , т.е. энергия .

Поток вектора магнитной индукции, пронизывающий площадку S - это величина, равная: Измряется в веберах (Вб) величина скалярная. Равен числу линий магнитной индукции, проходящих сквозь данную поверхность. Поток вектора магнитной индукции сквозь произвольную замкнутую поверхность равен нулю: Это теорема Остроградского-Гаусса для магнитного поля. Она свидетельствует о том, что в природе не существует магнитных зарядов – физических объектов, на которых бы начинались или заканчивались линии магнитной индукции.

магнитный дипольный момент — основная величина, характеризующая магнитные свойства вещества. Источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки. Элементарным источником магнетизма считают замкнутый ток. Магнитный момент измеряется в А⋅м² или Дж/Тл (СИ).В случае плоского контура с электрическим током магнитный момент вычисляется как где I — сила тока в контуре, S — площадь контура, — единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находится по правилу буравчика: если вращать ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика.Для произвольного замкнутого контура магнитный момент находится из:

,где — радиус-вектор, проведенный из начала координат до элемента длины контура

В общем случае произвольного распределения токов в сре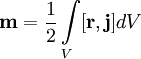де:

,где — плотность тока в элементе объёма dV.

№ 18. Магнитное поле в веществе .Намагниченность, напряженность магнитного поля ,магнитная восприимчивость, проницаемость, энергия магнитного поля. Диамагнетизм. Парамагнетизм. Ферромагнетизм .Петля гистерезиса. Условия на границе раздела двух магнетиком.

Для объяснения намагниченности тел Ампер предположил, что в молекулах вещества циркулируют круговые токи.. Каждый такой ток обладает магнитным моментом и создаёт в окружающем пространстве магнитное поле. В отсутствии внешнего поля магнитные токи ориентированы беспорядочным образом, вследствии чего обусловленное ими магнитное поле равно нулю. Под действием внешнего магнитного поля магнитные моменты молекул приобретают преимущественное направление, вследствие чего образец становится магнетиком, т.е. наманичивается –его суммарный магнитный момент становится отличным от нуля.

Для объяснения многих магнитных явлений используют квазиклассическую модель, в которой предполагается , что атом состоит из положительного ядра, вокруг которого вращаются электроны по круговым орбитам. Электроны, обращающиеся по орбитам ,представляют собой замкнутые электрические токи. Кроме орбитальных моментов, электрон обладает собственным механическим моментом импульса , называемый спином. Спину электрона соответствует собственный магнитный момент . Общий магнитный момент атома или молекулы равен векторной сумме магнитных моментов (орбитальных и спиновых) входящих в атом (молекулу) электронов:

.

Для количественного описания намагничивания магнетиков вводится векторная величина – намагниченность, определяемая магнитным моментом единицы объёма магнетика: , где – магнитный момент магнетика, равный векторной сумме магнитных моментов отдельных молекул. Вектор намагничения связан с напряжённостью магнитного поля: , где – магнитная восприимчивость, величина безразмерная. Магнитная восприимчивость — физическая величина, характеризующая связь между магнитным моментом (намагниченностью) вещества и магнитным полем в этом веществе.

Магнитное поле в веществе складывается из двух полей: внешнего поля , создаваемого намагничивающим током в вакууме, и поля намагниченного вещества , где , , тогда или , величина – называется магнитной проницаемостью вещества. Магнитная проницаемость — физическая величина, характеризующая связь между магнитной индукцией B и напряжённостью магнитного поля H в веществе. В общем случае зависит как от свойств вещества, так и от величины и направления магнитного поля.

Обычно обозначается греческой буквой μ.

Напряжённость магнитного поля- векторная физическая величина (Н), являющаяся количественной характеристикой магнитного поля. Н. м. п. не зависит от магнитных свойств среды. В среде Н. м. п. Н определяет тот вклад в магнитную индукцию В, который дают внешние источники поля , где j — намагниченность среды.

Единицей Н. м. п. в СИ является ампер на метр (а/м).