Второй закон термодинамики.

Запишем формулу Больцмана для энтропии: .λ- внешний параметр.

Пусть для рассматриваемой термодинамической системы зафиксирована не энергия, а температура, в этом случае вероятность состояний системы определяется каноническим распределением. Энергия в этом случае не имеет определенного значения, поэтому энтропия определяется, как средняя по каноническому распределению: , т.к. , то с достаточной точностью можно считать, что .

Полный дифференциал энтропии будет равен:

, .

Сравнив полученное равенство с первым законом термодинамики, приходим к выводу, что , откуда , .

При равновесном циклическом процессе .

Рассмотрим адиабатический равновесный процесс. Для него . В случае неравновесного адиабатического процесса .

Если энергия системы изменяется, как по средствам совершения работы, так и по средствам теплообмена, то в равновесном процессе , а в неравновесном .

Учитывая вышесказанное можно дать формулировку 2-го закона термодинамики, как закона изменения энтропии для произвольного процесса:

Существует функция состояния термодинамической системы, которая называется энтропией, и изменение которой определяется выражением . В случае конечного процесса энтропия определяется с точностью до постоянного слагаемого определяемого начальными условиями.

Изменение энтропии в круговом процессе равно нулю, откуда получаем неравенство Клаузиуса: , для любого термодинамического цикла. Из первого закона термодинамики: следует что - основное термодинамическое равенство для равновесных процессов.

Все неравновесные процессы являются необратимыми. Необратимость процесса означает, что после его совершения вначале в прямом направлении, затем в обратном направлении остаются изменения в окружающих телах.

Из 2-го закона термодинамики имеются следствия:

1. невозможно некоторое количество теплоты, взятое у какого-либо тела полностью превратить в работу без изменения состояния других объектов. (Кельвин).

Это означает, что всякая периодически действующая тепловая машина имеет 3 части: нагреватель, рабочее тело и холодильник .

2. невозможен вечный двигатель 2-го рода, т.е. периодически действующая тепловая машина, совершающая работу только за счет одного источника теплоты.

3. невозможен круговой процесс единственным результатом, которого является передача тепла от менее нагретого тела к более нагретому. (Клаузиус)

Рассмотрим цикл Карно:

Рассмотрим систему, в которой нагретое тело охлаждается, причем его внутренняя энергия переходит в работу, совершенную над другими телами (адиабатически изолированными). Оказывается можно превратить лишь часть теплоты в работу передавая другую ее часть третьим телам. Следствие из этого: всякая периодически действующая машина имеет три части: нагреватель, рабочее тело и холодильник. Теплота, взятая у нагревателя, передается рабочему телу, в котором совершается круговой процесс. Машина будет работать, если

Т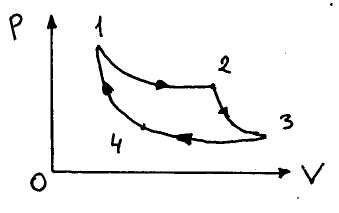 .е пока имеется разность температур нагревателя и холодильника. Рассмотрим цикл Карно, состоящий из двух изотерм и двух адиабат. В адиабатическом процессе система не получает и не отдает теплоту. Пусть Q₁ – теплота полученная системой при изотермическом процессе 1-2, а Q₂ теплота, отданная при изотермическом процессе 3-4.

1-2, 3-4 – изотермы

2-3, 4-1 – адиабаты.

Из неравенства Клаузиуса следует: .

, , .

Вывод:

Т. Карно

КПД всех равновесных машин Карно одинаков и зависит только от температуры нагревателя и холодильника.

КПД неравновесной машины всегда меньше КПД равновесной, работающей в том же интервале температур.

Рассмотрение цикла Карно позволяет ввести понятие абсолютного нуля температуры.

Абсолютный нуль температуры – температура холодильника обратимого цикла Карно с КПД равным 1.

№12 Микросостояния макроскопической системы. Статистическое распределение микросостояния. Флуктуации. Статистическое определение энтропии. Закон возрастания энтропии.

При изучении макроскопической системы в статистической физике исходят из определенной ее модели. Вначале выделяются элементарные структурные единицы, из которых построена система. Затем указывают, как они взаимодействуют друг с другом и как средствами классической или квантовой механики описывается движение частиц.

В статистической физике изучаются неупорядоченные, хаотические движения.

Будем рассматривать частицу как материальную точку. Пусть в каждый момент времени частица имеет определенное положение в пространстве и импульс, которые задаются векторами и . Одновременное задание 3N координат частиц и 3N импульсов определит микроскопическое состояние системы. С течение времени координаты, и импульс частиц изменяются, - следовательно, изменяются и микросостояние системы. В статистической физике движение системы описывается уравнениями Гаммельтона.

где (i=1,2..3N)

Функция Гаммельтона есть энергия системы, выраженная через обобщенные координаты и обобщенные импульсы H=E(q_i P_i). В декартовых координатах

где - параметр внешнего воздействия на систему.

Первое слагаемое есть суммарная кинетическая энергия частиц, второе – потенциальная энергия их взаимодействия друг с другом и внешними телами.

Статистические закономерности в системе появляются в том, что имеют место различные вероятности различных микросостояний, вместе с ними вероятности для значений физических величин, описывающих всю систему в целом.

Совокупность чисел W_i образует распределение вероятностей для состояния системы, которое имеет вид:

Где - время пребывания системы в i- состоянии. – большой период времени

Введем понятие статистического ансамбля систем. Обозначим n_i число систем в I – квантовом состоянии и через N – число членов ансамбля. Тогда вероятность обнаружения системы в заданном состоянии равна

Закон распределения вероятностей для ансамбля систем будет тем же, что и для временной последовательности состояния системы. Это положение называется эргодинамической гипотезой и составляет один из исходных принципов статистического метода.

Зная функцию распределения вероятностей микроскопических состояний, можно вычислить среднее значение физических величин – микроскопические характеристики системы. Пусть имеется дискретный ряд состояний, при которых величина L принимает значение L_i с вероятностью W_i , тогда среднее значение , Сумма берется по всем допустимым квантовым состояниям системы. Распределение вероятностей W_i должно быть нормировано условием

Микросостояния с течением времени изменяются, и это приводит к изменению физических характеристик системы. Для количественной оценки отклонений от среднего вводится квадратичная флуктуация (среднеквадратичное отклонение)

Чем меньше квадратичная флуктуация, тем ближе среднее значение к мгновенным. Это означает, что большие отклонения L от встречаются редко и они маловероятны. Значения отклонений от среднего характеризуется относительной флуктуацией:

или - соотношение является частным случаем общей закономерности: статистический метод применим лишь к системам состоящим из большого числа частиц

Всякому микросостоянию соответствует набор микросостояний, с ним совместимых. Назовем термодинамической вероятностью макроскопического состояния величину, равную числу микросостояний системы, посредством которых данное макросостояние осуществляется. Обозначим термодинамическую вероятность W_T

W_T=Ω (омега). Число микросостояний Ω называется статистическим весом макросостояния.

Если исходить из допущения равновероятности всех микросостояний произвольной изолированной системы, то справедливо утверждение: вероятность осуществления макроскопического состояния системы пропорциональна числу микросостояний, с ним совместимы

Величина - называется энтропией системы, К – постоянная Больцмана.

Энтропия для полосы энергий шириной определяется формулой

Где Ω(E) – число состояний при всех энергиях от 0 до E. Учитывая объем ячейки (Г) в фазовом пространстве, приходящей на одно квантовое состояние, имеем:

f- число степеней свободы

и

В классической статистике для заданной энергии системы полагают:

Энтропия S_кл всегда определяется с точностью до аддитивной постоянной.

Представленная самой себе замкнутая система будет переходить от менее вероятных состояний к более вероятным состояниям, пока не достигнет наиболее вероятного, равновесного состояния. В то же время будет расти энтропия системы. В равновесии она имеет максимум.

Теорема Нернста, недостижимость абсолютного нуля.

Нернст доказал теорему, которая дает возможность определить значение энтропии в любом состоянии.

Теорема Нернста формулируется так, что при стремлении абсолютной температуры к нулю энтропия любого тела также стремиться к нулю:

Согласно теореме Нернста энтропия любого тела при абсолютном нуле равна нулю. На этом основании энтропия в состоянии с температурой T может быть представлена следующим образом:

Если известна, например теплоемкость тела при постоянном давлении, как функция температуры, то энтропия может быть вычислена по формуле

№ 13. Агрегатное состояние вещества. Характер теплового движения молекул и свойства вещества в различных агрегатных состояниях. Равновесие фаз, фазовые переходы. Уравнение Клапейрона-Клаузиуса.

В природе существует три агрегатных состояния вещества: твёрдое, жидкое и газообразное. Молекулярная физика основана на молекулярно-кинетической теории строения вещества. Согласно этой теории все тела состоят из частиц – атомов, молекул, находящихся в непрерывном хаотическом движении, которое называется тепловым движением. Тепловое движение частиц вещества в различных агрегатных состояниях не одинаково. Оно зависит от сил притяжения и отталкивания, действующих между молекулами и атомами.

Сила притяжения между атомами и молекулами достаточно разряжённых газов практически отсутствуют; частицы таких газов находятся друг от друга на расстояниях превышающий радиус молекулярного действия. Частицы таких газов движутся равномерно и прямолинейно до тех пор, пока они не столкнутся между собой и стенками сосуда. Эти столкновения носят случайный характер. При взаимодействии молекулы изменяют произвольным образом направление своего движения. В итоге тепловое движение молекул газов является беспорядочным и в среднем в любом произвольном направлении внутри газа в любой момент времени движется одинаковое число молекул.

Твёрдые кристаллические тела характеризуются значительными силами взаимодействия между частицами твёрдых тел (атомами, молекулами). Совместное действие сил притяжения и отталкивания между этими частицами приводит к тому, что частицы твёрдых тел совершают колебания около средних равновесных положений – узлов кристаллической решётки.

Тепловое движение молекул жидкости имеет промежуточный характер между движениями частиц в газах и твёрдых телах. Молекула жидкости определённое время колеблется около некоторого положения равновесия и находится в оседлом положении. По истечении некоторого времени положение равновесия молекулы смещается и образуется новое осёдлое положение. Происходят одновременно медленное перемещение молекул и их колебания внутри малых объёмов.

Фазой называется термодинамическое равновесное состояние вещества, отличающееся от других возможных равновесных состояний того же вещества. Переход вещества из одной фазы в другую называется фазовым переходом. Он всегда связан с качественным изменением свойств вещества.

Фазовый переход первого рода – это переход, сопровождающийся поглощением или выделением теплоты (плавление, кристаллизация). Он характеризуется постоянством температуры, изменениями энтропии и объёма.

Фазовый переход второго рода – переход не связанный с поглощением или выделением теплоты и изменением объёма. Он характеризуется постоянством объёма и энтропии, но скачкообразным изменением теплоёмкости.

Е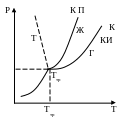 сли система является химически однородной, то понятие фазы совпадает с понятием агрегатного состояния.

Для наглядного изображения фазовых превращений используется диаграмма состояний, на которой в координатах (Р,Т) задаётся зависимость между температурой фазового перехода и давлением в виде кривых.

КИ – испарение, КП – плавление, сублимация. ТТ – твёрдая фаза, Ж – жидкая и Г ­– газообразная. Кривые на диаграмме называются кривыми фазового равновесия, каждая их точка соответствует условиям равновесия двух существующих фаз.

Тройной точкой называется точка, в которой пересекаются крвые фазового равновесия и которая определяет условия (Р_тр, Т_тр) одновременного существования трёх фаз вещества.

Уравнение Клапейрона-Клаузиуса позволяет определить наклоны кривых. Здесь L – теплота фазового перехода, (V₂ – V₁) – изменения объёма вещества при переходе из первой во вторую фазу, T – температура перехода.

Поскольку L и T всегда положительны, то наклон кривой равновесия определяется знаком (V₂ – V₁). Так при испарении и сублимации объём всегда возрастает, поэтому . К – критическая точка, на кривой испарения. Поэтому возможен непрерывный переход вещества из жидкого состояния в газообразное и обратно, который не сопровождается фазовыми превращениями.

№14 Электрический заряд. Дискретность заряда. Закон Кулона. Объемная, поверхностная, линейная плотность заряда. Измерение элементарного заряда(опыт Миллекена-Иоффе) и удельного заряда частиц( опыт Томсона). Закон сохранения заряда( уравнение непрерывности).

Электрический заряд — физическая величина, определяющая интенсивность электромагнитного взаимодействия.

Свойства заряда:

1. Носителями электрического заряда являются заряженные эле­ментарные частицы — протон и электрон. Заряженные частицы взаимодействуют между собой с силами, убывающими с расстоянием так же медленно, как гравитационные, но во много раз превышающими их по величине.

2. Все заряженные элементарные частицы обладают одним и тем же по величине зарядом, который называют элементарным зарядом и обозначают буквой е. Опыт показывает, что заряд элементарных частиц не зависит от их скорости.

3. Заряд элементарных частиц может быть положительным или от­рицательным. Одноименные частицы отталкиваются, разноименные — притягиваются. За положительный заряд принят заряд протона +е. Заряд электрона —отрицательный (—е). Заряд электрона - 1,6^. 10^-19 Кл, Масса электрона 9,1 ^. 10^{-31 кг}

Если в состав макроскопического тела входит различное количество электронов N_e и протонов N_P, то оно оказывается заряженным. Заряд тела всегда представляется числом, кратным величине элементарного заряда: q = e(N_p — N_e).Дискретность заряда: любой электрический заряд является кратным элементарному заряду е.

Закон сохранения электрического заряда гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется.

Закон Кулона описывает взаимодействие покоящихся точечных зарядов, т.е. элементарных частиц или заряженных тел, размеры ко­торых малы по сравнению с расстоянием между ними. Сила взаимо­действия двух точечных зарядов в вакууме (кулоновская сила) прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними: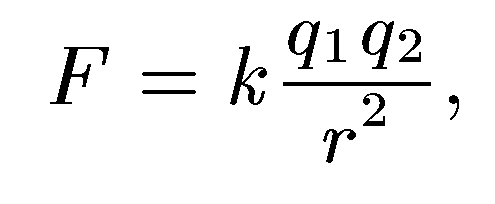 где к — коэффициент пропорциональности, зависящий от системы еди­ниц. Сила взаимодействия направлена вдоль прямой, соединяющей зарядыВ СИ единица заряда кулон (Кл) определяется через еди­ницу силы тока ампер, а коэффициент в формуле (1) равен к = 9,0 х 10⁹ Н • м²/Кл²

или эл.постоянная

Распределение заряда по пространству задается пространственной плотностью заряда ρ(r), по поверхности — поверхностной плотно­стью заряда σ(r), по линии — линейной плотностью заряда λ (r): dq = ρdV, dq = σdS, dq =λdl.

Опыт Милликена. доказательство существования элементарного электрического заряда было дано опытами, которые выполнил Милликен. В этих опытах измерялась скорость движения капель масла в однородном электрическом поле между двумя металлическими пластинами. Капля масла, не имеющая электрического заряда из-за сопротивления воздуха падает с некоторой постоянной скоростью. Если на своем пути капля встречается с ионом и приобретает электрический заряд q, то на нее, кроме силы тяжести, действует еще кулоновская сила со стороны электрического поля. В результате изменения силы, вызывающей движение капли, изменяется скорость ее движения. Измеряя скорость движения капли и зная напряженность электрического поля, в котором происходило ее движение, Милликен мог определить заряд капли.    Опыт Милликена был повторен Иоффе. В опытах Иоффе для определения элементарного электрического заряда вместо капель масла использовались металлические пылинки. Изменением напряжения между пластинами достигалось равенство кулоновской силы и силы тяжести (рис. 163), пылинка в этом случае была неподвижной:

При освещении пылинки ультрафиолетовым светом ее заряд изменялся и для уравновешивания силы тяжести нужно было изменить напряженность электрического поля между пластинами: .По измеренным значениям напряженности электрического поля можно было определить отношение электрических зарядов пылинки: ;

,    ,    ...,    .Опыты Милликена и Иоффе показали, что заряды капель и пылинок всегда изменяются скачкообразно. Минимальная «порция» электрического заряда — элементарный электрический заряд, равный .В своем опыте Томсон использовал усовершенствованную катодно-лучевую трубку, конструкция которой была дополнена электрическими катушками, создававшими внутри трубки магнитное поле, и набором параллельных электрических конденсаторных пластин, создававших внутри трубки электрическое поле. Благодаря этому появилась возможность исследовать поведение катодных лучей под воздействием и магнитного, и электрического поля. Проведя ряд измерений, Томсон определил скорость движения катодных лучей. Оказалось, что они движутся значительно медленнее скорости света, из чего следовало, что катодные лучи могут быть только частицами, т.к.любое электромагнитное излучение распространяется со скоростью света. Эти неизвестные частицы Томсон назвал корпускулами, но вскоре они стали называться электронами.

№ 15. Электростатическое поле в вакууме его потенциальность. Принцип суперпозиции и теорема Остроградского-Гаусса; их применимость к решению задач. Энергия взаимодействия системы зарядов и энергия электростатического поля. Электроемкость.

Электростатическим полем называется поле, создаваемое неподвижными электрическими зарядами. Электростатическое поле описывается двумя физическими величинами: потенциалом (энергетическая скалярная характеристика) и напряжённостью (векторная силовая характеристика).

Потенциалом электростатического поля называется физическая величина, равная отношению потенциальной энергии пробного точечного электрического заряда, помещенного в рассматриваемую точку поля, к этому заряду q. . Потенциалы электростатического поля одного точечного заряда q_i и системы из n точечных зарядов в вакууме равны , . Т. о. , т.е при наложении электростатических полей их потенциалы складываются алгебраически.

Напряжённость– векторная величина, определяемая отношением силы действующей на единичный положительный заряд q₀, помещённый в данную точку к величине этого заряда; вычисляется по формуле . Напряжённость поля точечного заряда , в диэлектрике , в скалярной форме и , .Графически электростатическое поле изображается с помощью линий напряжённости. Линиям напряжённости приписывается направление, совпадающее с направлением вектора напряжённости. Так как в данной точке пространства вектор напряжённости имеет лишь одно направление, то линии напряжённости никогда не пересекаются.

Примеры.

Н апряжённость результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряжённостей полей создаваемых в данной точке каждым зарядом в отдельности, т.е. . Эта формула выражает принцип суперпозиции электростатических полей.

Теорема Остроградского-Гаусса. позволяет вычислить напряжённости поля системы электрических зарядов с помощью принципа суперпозиции электростатических полей. Теорема определяет поток вектора напряжённости электрического поля сквозь замкнутую поверхность.

Рассмотрим поток вектора напряжённости через сферическую поверхность радиуса r, охватывающую точечный заряд q, находящийся в её центре . Этот результат справедлив для любой точки замкнутой поверхности произвольной формы, охватывающей заряд. Рассмотрим общий случай произвольной поверхности, охватывающее n зарядов.

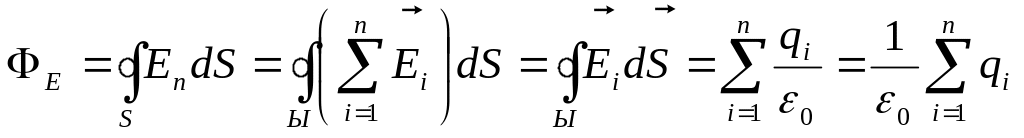
Поток вектора напряжённости электростатического поля в вакууме сквозь произвольную поверхность равен алгебраической сумме заключённого внутри, этой поверхности зарядов, делённых на ( – электрическая постоянная).

Примеры.