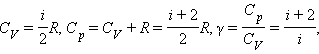Экспериментальные основы с.Т.О. Постулаты Эйнштейна. Пространство время и системы отсчета в с.Т.О. Преобразование Лоренца и их кинематические следствия.

Специальная теория относительности (С.Т.О.) представляет собой современную физическую теорию пространства и времени. Она предложена А. Эйнштейном для согласования экспериментальных данных по измерению скорости света с теоретической базой классической механики. Согласно классическим преобразованиям Галилея, скорость света зависит от скорости источника света. Если источник света движется равномерно со скоростью υ, то для неподвижного наблюдателя результирующая скорость света C должна быть равна C= c+υ где с – скорость света в вакууме. Майкельсон провел опыт по определению разности скорости света вдоль и поперек движения Земли, предполагая, что эта разность будет равна скорости движения земли по орбите но опыт дал отрицательный результат разность скоростей равна нулю, т.е. скорость света с не зависит от скорости источника света υ. Такой результат не мог объясняться в рамках классической механики.

Постулаты Эйнштейн.

1. В любых инерциальных системах отсчета все физические явления протекают одинаково при одних и тех же условиях

2. Скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит ни от скорости источника, ни от скорости приемника света

Первый постулат является обобщением механического принципа относительности Галилея на все физические процессы. Этот постулат называется принципом относительности.

Постулаты С.Т.О. противоречат тем представлениям о свойствах пространства и времени, которые приняты в классической механике.

В механике Ньютона считается утверждением об одинаковости хода времени во всех инерциальных систем отсчета, а также абсолютности промежутка времени между двумя событиями. В С.Т.О. ход времени в разных инерциальных системах различен. Соответственно промежуток времени, между какими – либо двумя определенными событиями относителен; он изменяется при переходе от одной инерциальной системе отсчета к другой. В частности, относительна одновременность двух событий происходящих в разных точках пространства. В одних системах отсчета первое из этих двух событий раньше второго, а других позже второго.

Преобразование Лоренца и их кинематические следствия.

Из постулатов С.Т.О. , а также из однородности к изотропности пространства и однородности времени следует, что соотношение между координатами и временем одного и того же события в двух инерциальных системах отсчета выражаются преобразованиями Лоренца.

Преобразование Лоренца имеют простейший вид, если сходственны оси декартовых координат неподвижной (K) и подвижной ( ) инерциальных систем попарно параллельны, движется относительно K с постоянной скоростью υ вдоль оси OX.

Где ;

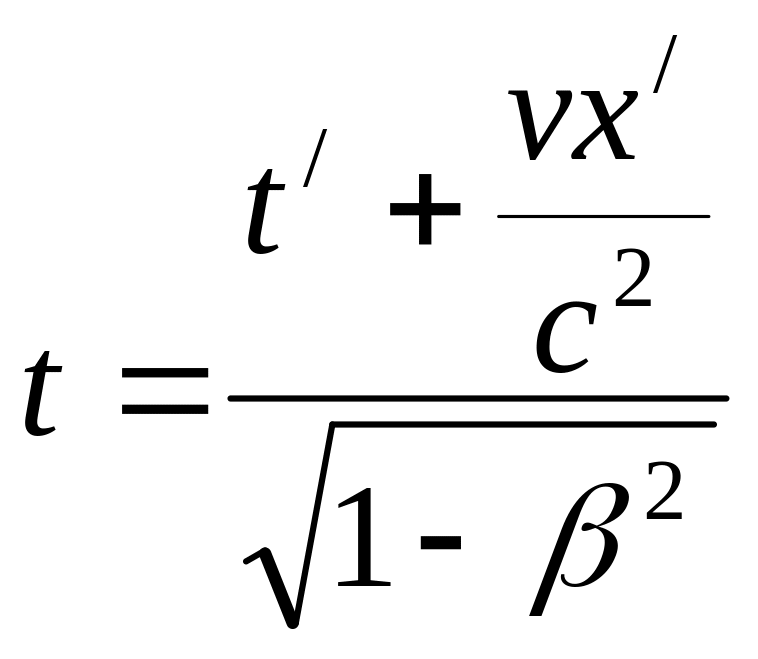
Эти соотношения при υ<<c переходят в преобразования Галилея. Преобразования Лоренца устанавливают взаимосвязь пространства и времени - в закон преобразования координат входит время, а в закон преобразования времени – пространственные координаты.

Следствия:

А) Релятивистский закон сложения скоростей имеет вид

U – Скорость материальной точки относительно подвижной системы отсчета,

- Скорость подвижной системы отсчета относительно неподвижной

- Скорость материальной точки относительно неподвижной системы отсчета

Скорость свет – инвариантна в преобразованиях Лоренца. Например, если источник света, излучает свет, движется в системе со скоростью С, то для наблюдателя в системе

Скорость света в вакууме – есть предельная скорость передачи сигнала. Относительность длины: длина l - тела, движущегося со скоростью , меньшей собственной длины l₀ тела

;

Движущееся тело сокращает длину вдоль направления движения. Размеры тела в направлении перпендикулярно движению неизменны.

Релятивистский интервал времени в неподвижной системе отсчета:

Движущиеся часы идут медленнее неподвижных

№7 Релятивистские импульс и энергия,связь между ними.Энергия покоя. Частицы с нулевой массой. Второй закон Ньютона в СТО. Закон сохранения энерги –импульса

Из теории относительности следует, что уравнение динамики, инвариантное по отношению к преобразованиям Лоренца, имеет вид:

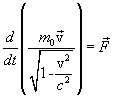(1) где - инвариантная, т.е. одинаковая во всех системах отсчета величина называемая массой покоя частицы, v- скорость частицы, - сила действующая на частицу. Сопоставим с классическим уравнением Мы приходим к выводу, что релятивистский импульс частицы равен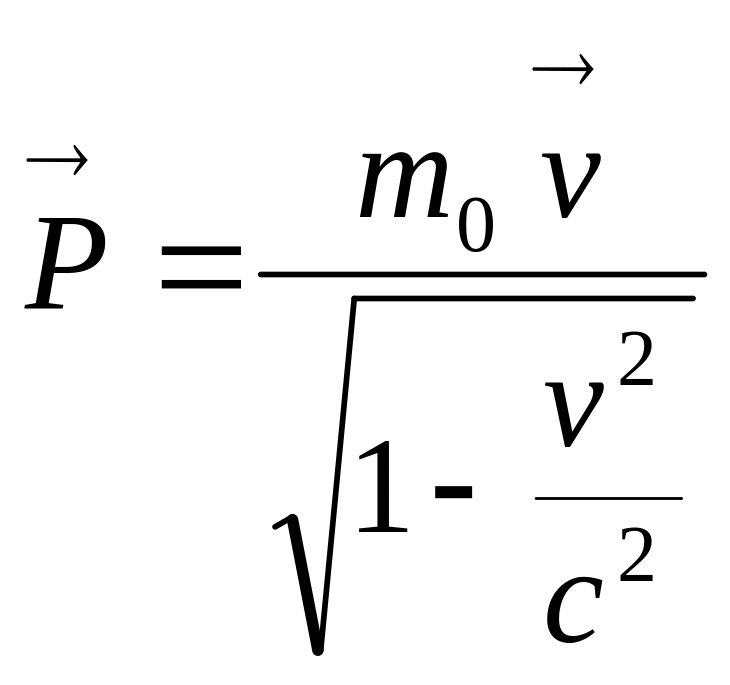 .Пусть на свободное тело с массой покоя m₀ действует полная сила F. Подсчитаем работу этой силы. Элементарная работа на перемещении dl равна: dA=Fdl, где F определяется (1).Опуская выкладки, запишем выражение для работы:

где и — скорость тела; G — постоянная интегрирования, а Мы предполагали, что изменения массы покоя т₀ не происхо­дит. Поэтому можно считать, что работа А полной силы идет исключительно на сообщение телу кинетической энергии:

Постоянную G определим из условия, что при и = О кинетиче­ская энергия тела также равна нулю (Т = 0).Получаем:

Тогда формула для кинетической энергии принимает вид: или, если ввести релятивистскую массу

Кинетическая энергия выступает как разность энергий, ко­торыми обладает тело в состоянии движения и в состоянии по­коя. Движущееся тело обладает энергией, которая зависит от релятивистской массы. Вывод: в каком бы со­стоянии тело ни находилось, оно обладает полной релятивист­ской энергией

Если тело покоится (и=0), то его энергия равна Е₀ = m ₀с².Наличие энергии покоя позволяет рассматри­вать всякое тело как некий ре­зервуар потенциальной энер­гии, которая может обратиться в любые другие виды энергии. При этом не имеет никакого значения внутреннее строение тела: оно может быть простым (элементарная частица) или сложным (атом; кристалл;). Cмысл формулы: формула указывает максимальную энергию, которая мо­жет быть получена от тела с массой покоя m₀, если это тело целиком преобразуется в материальный объект, лишенный массы покоя, т. е. в электромагнитное излучение тела.

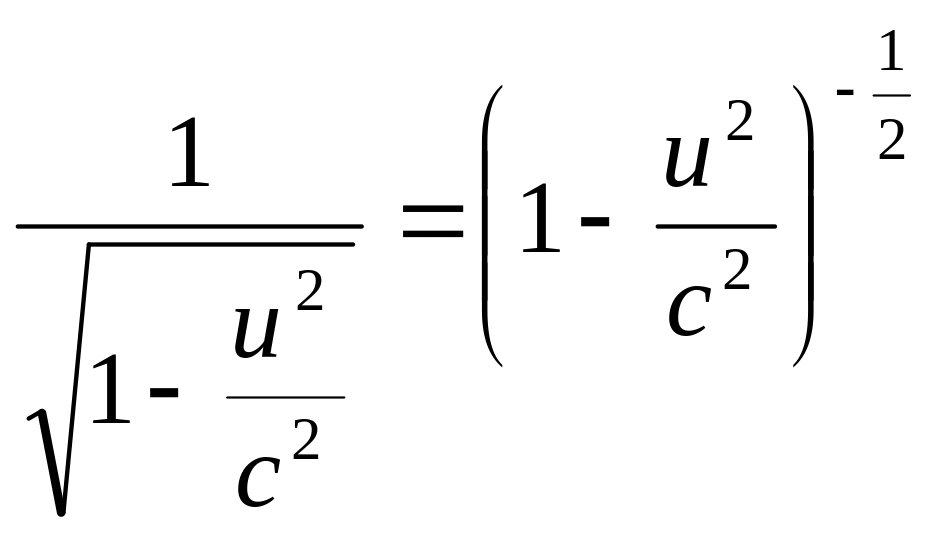Выразим релятивист­скую кинетическую энергию Т из равенства , когда скорость тела не велика: , можно выражение разложить по формуле бинома Ньютона: и ограничиться первыми двумя членами разложения

А это обычная (нерелятивистская) формула кинетической энер­гии.

Мы видим, что обычная формула для кинетической энергии оказывается справедливой лишь при малых скоростях. Точное же значение Т при любых скоростях (при т₀ = const) рассчи­тывается по релятивистской формуле.

Связь энергии с импульсом:

Энергия тела и его импульс связаны с релятивистской массой

соотношениями ,

где и — скорость тела. Возведем оба равенства в квадрат, после чего второе умножим на с²: ,

Вычтя из первого уравнения второе и подставляя выражение для релятивистской массы получаем: искомую связь энергии с импульсом:

Масса покоя т₀ и скорость света в вакууме с имеют во всех инерциальных системах неизменные значения. Они ин­вариантны к преобразованиям Лоренца. Энергия Е и импульс р изменяются при переходе от одной инерциальной системы отсчета к другой. разность Е² — р²с² сохраняется во всех системах отсчета. Т.о., величина Е² — р²с² инвариант­на к преобразованиям Лоренца. В этом состоит особен­ность связи между Е² и р²с².

Выразим из релятивистскую энергию Е:

Отсюда следует, что релятивистской энергией обладают и такие тела, которые не имеют массы покоя (т₀ = 0). В настоящее время известны две такие частицы: фо­тон и нейтрино.

Закон сохранения энергии-импульса:

В релятивистской механике следует различать два вида си­стем: системы, в которых тела не взаимодействуют, и системы, в которых они взаимодействуют.

Для систем первого вида полная релятивистская энергия и импульс будут равны суммам реляти­вистских энергий и импульсов отдельных тел:

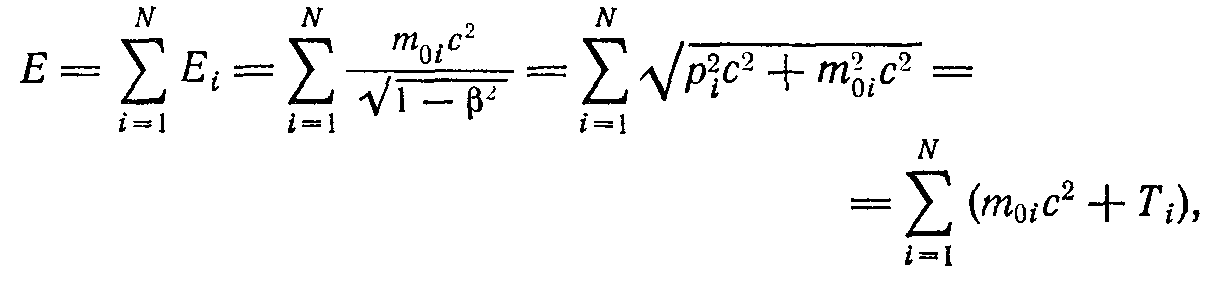
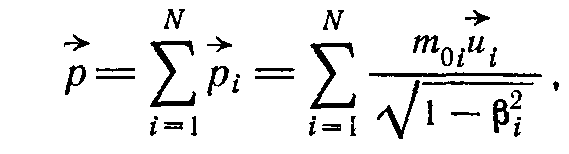
N- число тел составляющих систему

Поскольку тела не взаимодействуют, скорости отдельных тел и их релятивистская энергия будут постоянны. Поэтому постоян­ными будут также полная энергия и полный импульс системы.

Если же система состоит из N взаимодействующих тел, то оказывается невозможным записать выражение для полной энер­гии системы, т.к. невозможно записать потенциальную энер­гию взаимодействия, когда тела движутся, а взаимодействие между ними распространяется с конечной скоростью с.

Однако если взаимодействие носит характер соударения, то выражения для энергии системы и импульса можно записать для тех моментов времени, когда взаимодействие еще не начиналось или уже окончилось, т. е. до соударения или после соударения. Так как система замкнута, то ни энергия, ни импульс системы изменяться не будут:

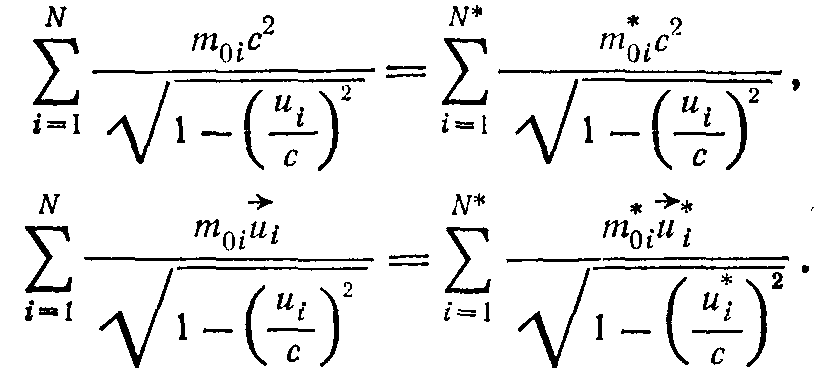
Здесь звездочкой * отмечены величины, которые относятся к мо­менту после соударения. Заметим, что число тел в системе до и после соударения может быть различным (N не= N*). Это на­блюдается при взаимодействии частиц микромира.

№ 8. Молекулярно-кинетическая теория газов. Идеальный газ. Параметры состояния. Уравнения состояния для идеального газа. Температура. Внутренняя энергия.Теплота и работа. Первое начало термодинамики.

Газ – это совокупность хаотически движущихся, невзаимодействующих друг с другом на расстоянии молекул. Размеры молекул столь малы, что суммарным объёмом можно пренебречь по сравнению с объёмом сосуда. Большую часть времени каждая молекула движется свободно, претерпевая иногда соударения с другими молекулами или стенками сосуда. Такая модель представляет собой идеальный газ.

Основное уравнение кинетической теории газов имеет вид , где – число молекул в единице объёма, m₀ – масса одной молекулы газа, – средняя квадратичная скорость в квадрате.

Учитывая, что – кинетическая энергия поступательного движения молекулы, выражение для давления имеет вид: . Согласно этому уравнению давление равно двум третям кинетической энергии поступательного движения молекул, заключённых в единице объёма.

Т. к. средняя кинетическая энергия молекул равна , то давление может быть выражено и такой формулой , где k =1,38*10^-23Дж/К– постоянная Больцмана, Т – температура по абсолютной шкале.

Параметры состояния системы разделяются на внешние и внутренние. Внешними параметрами системы называются физические величины, которые зависят от положения в пространстве и различных свойств тел, являющихся внешними по отнеошению к данной системе, например, объём V для газа.

Внутренними параметрами системы называются физические величины, зависящие как от положения по отношению к системе тел, так и от координат и скоростей частиц, образующих данную систему, например, давление газа и его энергия.

Уравнением состояния простой системы называется функциональная зависимость равновесного давления P в системе от объёма и температуры P=f(V,T).

Уравнение состояния для моля – Клапейрона имеет вид PV=RT, где R=8,31Дж/моль К – универсальная газовая постоянная.

Уравнение Менделеева-Клапейрона – урвнение состояния для любой массы вещества идеального газа . Это уравнение можно преобразовать, учтя , , , . Таким образом:

1. давление идеального газа при данной температуре прямо пропорционально концентрации его молекул.

2. при однинаковых температуре и давлении все газы содержат в единице объёма одинаковое число молекул.

Число молекул, содержащихся в 1 м³ при нормальных условиях называется числом Лошмидта .

Температура- мера средней кинетической энергии поступательного движения молекул.

В настоящее время используют две температурные шкалы. Международная практическая шкала( шкала Цельсия) градуированная в градусах Цельсия по двум реперным точкам- температурам замерзания и кипения воды при давлении 10⁵Па которые принимаются соответственно 0⁰С и 100⁰С.Термодинамическая температурная шкала (шкала Кельвина) градуированная в градусах Кельвина определяется по одной реперной точке- тройной точке воды- температуре при которой лед, вода и насыщенный пар при давлении 609 Па находятся в термодинамическом равновесии. Температура этой точки равна 273 К.

Внутренняя энергия тела (обозначается как E или U) — полная энергия этого тела за вычетом кинетической энергии тела как целого и потенциальной энергии тела во внешнем поле сил. Следовательно, внутренняя энергия складывается из кинетической энергии хаотического движения молекул, потенциальной энергии взаимодействия между ними и внутримолекулярной энергии.Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.

Теплота и работа. Теплотой называется такая форма передачи энер­гии, при которой осуществляется непосредственный об­мен энергией между хаотически движущимися частицами взаимодействующих тел. Процесс передачи внутренней энергии без совершения работы называется теплообменом. Мерой энергии, пере­данной в форме теплоты в процессе теплообмена, служит величина, называемая количеством теплоты.

О работе можно говорить тогда, когда происходит изменение состояния тела. Различаются работа А, которая совершается, системой над внешними телами, и работа А', которая совершается внешними телами над системой. Эти работа. численно равны и противоположны по знаку: А = - А'. Работа А принимается по­ложительной, работа A' отрицательной. Элементарная работа равна: А=рΔV. Теплота, как и работа,. является не видом энер­гии, а формой ее передачи.

Если над телом совершается работа, то это может привести к увеличению любого вида энергии данного тела или дру­гих тел.

Существует несколько эквивалентных формулировок первого начала термодинамики Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил

Q = ΔU+А _газа

Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами ΔU= Q-A Первый закон термодинамики применительно к изотермическому процессу в идеальном газе имеет вид ΔQ = А. Внутренняя энергия идеального газа ^; при этом изменяться не будет, т.к. ΔT = Т₂ — Т₁= 0 и Δ U= 0 Все подведенное количество теплоты расходуется на работу против внешнего дав­ления.

При изохорном процессе количество теплоты ΔQ идет только на увеличение внутренней энергий газа ΔU, ΔQ = ΔU. Следовательно, температура газа повышается на ΔT. Работу расширения газ не совершает (А= 0).При изобарическом процессе количество теплоты, подводимое к газу, расходуется и на увели­чение внутренней энергии и на работу расширения, ко­торую совершает газ против внешнего давления: ΔQ ==ΔU + A. При адиабатическом процессе ΔQ = 0 и первый закон термодинамики принимает вид А = -ΔU. В условиях отсутствия теплообмена с внеш­ней средой работа, которую производит тело против внешних сил, происходит за счет убыли его внутренней энергии.

Первый закон термодинамики утверждает, что не­возможно построить такой периодически действующий двигатель, который совершил бы работу большую, чем энергия, которая подводится к двигателю извне: веч­ный двигатель первого рода невозможен.Действительно, если в периодически действующем двигателе газ, пар или другое рабочее тело совер­шает круговой процесс , то изменения его внутренней энергии не происходит , ΔU = 0 и А = ΔQ . Работа, совершаемая этим телом, не может превосходить подведенного к нему количества теплоты.

№9Система в термостате. Распределение по энергии. Закон равнораспределения энергии по степеням свободы классической системы. Распределение Больцмана. Распределение Максвелла по скоростям для классической системы.

Система в термостате – это система, обменивающаяся тепловой энергией с другими системами, но сохраняющая при этом постоянную температуру.

Молекулу одноатомного газа можно рассматривают как материальную точку. Основанием для этого является то, что масса такого атома сосредоточена практически целиком в ядре, имеющем весьма малые размеры. Молекула одноатомного газа имеет три степени свободы поступательного движения. Числом степеней свободы механической системы называется количество независимых величин, с помощью которых может быть задано положение системы в пространстве. Средняя кинетическая энергия молекулы, движутся со скоростью (средняя квадратичная):

Эта энергия, ввиду хаотичности теплового движения молекул, равномерно распределяется между тремя степенями свободы, на каждую степень свободы поступательного движения одноатомной молекулы приходится одинаковая кинетическая энергия.

K =1,38*10^-23 Дж\К- постоянна Больцмана ,T – абсолютная температура

Законы равномерного распределения энергии по степеням свободы; на каждую степень свободы молекулы в среднем приходится одинаковая кинетическая энергия, равная 1/2KT.

Если молекула имеет i степеней свободы, то ее средняя кинетическая энергия

Закон равномерного распределения энергии по степеням свободы приводит к выводу о равноправности всех степеней свободы молекулы. Все они вносят одинаковый вклад в ее среднюю энергию. Этот вызов имеет ограниченную область применимости и пересмотрен в квантовой статистике.

В однородном поле тяготения Земли тепловое движение молекул приводит к некоторому стационарному состоянию газа, при котором давление газа с высотой убывает. Давление на высоте h газа с молярной массой μ, p_o нормальное давление равно

Используя соотношение

R=8,31 дж\моль К

Получаем

n_o – число молекул в единицу объема на высоте h=0, n- число молекул на высоте h

Так как

Потенциальная энергия молекулы в поле тяготения

Данное распределение называют распределение Больцмана.

Распределение частиц по значениям потенциальной энергии для внешнего потенциального поля .

Отношение n₁ к n₂ в точках, где потенциальная энергия молекулы имеет значения W_p1 и W_p2 равно

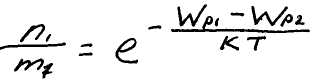
При постоянной температуре плотность газа больше там, где меньше потенциальная энергия молекул. Если частицы имеют одинаковую массу и находятся в хаотическом тепловом движении, то распределение Больцмана справедливо в любом внешнем потенциальном поле, а не только в поле силы тяжести.

В газе, находящемся в состоянии равновесии при данной температуре устанавливается некоторое стационарное не меняющееся со временем распределение молекул по скоростям. Это распределение описывается функцией f(υ), называемой распределения молекул по скоростям, которая определяет относительное число молекул, скорости которых лежат в интервале от υ до υ+dυ т.е.

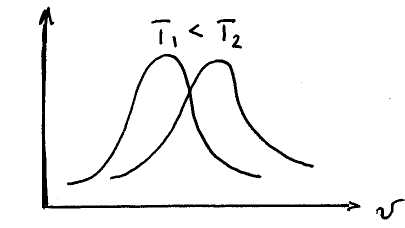
Закон Максвелла

Эта функция удовлетворяет условию нормирования

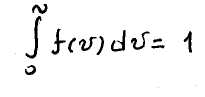Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называют наиболее вероятной скоростью υ_в пусть

получим

С повышением температуры скорость υ_в – растет (график)

№10 Классический идеальный газ и его свойства. Классическая теория теплоемкости идеального газа. Понятие о квантовой теории теплоемкости газа.

Идеальным газом является физическая модель согласно которой :

1. молекулы не взаимодействуют друг с другом на расстоянии

2. при взаимных столкновениях и соударениях со стеками сосуда молеку­лы идеального газа ведут себя как абсолютно упругие шары с диамет­ром d (эффективный диаметр молекулы), зависящим от химической природы газа.

3. межмолекулярные силы притяжения быстро убывают с увеличением расстояния г между молекулами и практически не проявляются.

Если в результате теплообмена телу передается некоторое количество теплоты, то внутренняя энергия тела и его температура изменяются. Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c.

Во многих случаях удобно использовать молярную теплоемкость C:

где M – молярная масса вещества.

Обычно рассматриваются два значения теплоемкости газов: C_V – молярная теплоемкость в изохорном процессе (V = const) и C_p – молярная теплоемкость в изобарном процессе (p = const).

В процессе при постоянном объеме A = 0. Из первого закона термодинамики для 1 моля газа следует

QV = CVΔT = ΔU.

Изменение ΔU внутренней энергии газа прямо пропорционально изменению ΔT его температуры.

Для процесса при постоянном давлении первый закон термодинамики дает:

Qp = ΔU + p(V2 – V1) = CVΔT + pΔV,

где ΔV – изменение объема 1 моля идеального газа при изменении его температуры на ΔT. Отсюда следует:

Отношение ΔV / ΔT может быть найдено из уравнения состояния идеального газа, записанного для 1 моля:

pV = RT,

где R – универсальная газовая постоянная. При p = const

Соотношение, выражающее связь между молярными теплоемкостями C_p и C_V, имеет вид

Cp = CV + R.

Отношение теплоемкостей в процессах с постоянным давлением и постоянным объемом обозначается греческой буквой γ.

Термодинамические процессы, в которых теплоемкость газа остается неизменной, называются политропическими. Все изопроцессы являются политропическими. В случае изотермического процесса ΔT = 0, поэтому C_T = ∞. В адиабатическом процессе ΔQ = 0, следовательно, C_ад = 0. В молекулярно-кинетической теории устанавливается следующее соотношение между средней кинетической энергией поступательного движения молекул и абсолютной температурой T:

При изменении температуры на ΔT внутренняя энергия изменяется на величину

Коэффициент пропорциональности между ΔU и ΔT равен теплоемкости C_V при постоянном давлении:

В классической статистической физике доказывается так называемая теорема о равномерном распределении энергии по степеням свободы:

Если система молекул находится в тепловом равновесии при температуре T, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна . Из этой теоремы следует, что молярные теплоемкости газа C_p и C_V и их отношение γ могут быть записаны в виде

где i – число степеней свободы газа.

Теорему о равномерном распределении энергии по степеням свободы можно применить и к тепловому движению частиц в твердом теле. Атомы, входящие в состав кристаллической решетки, совершают колебания около положений равновесия. Энергия этих колебаний и представляет собой внутреннюю энергию твердого тела. Каждый атом в кристаллической решетке может колебаться в трех взаимно перпендикулярных направлениях. Следовательно, каждый атом имеет 3 колебательные степени. При гармонических колебаниях средняя кинетическая энергия равна средней потенциальной энергии. Поэтому в соответствии с теоремой о равномерном распределении на каждую колебательную степень свободы приходится средняя энергия kT, а на один атом – 3kT. Внутренняя энергия 1 моля твердого вещества равна:

U = 3NAkT = 3RT.

Поэтому молярная теплоемкость вещества в твердом состоянии равна:

C = 3R = 25,12 Дж/моль·К.

Это соотношение называется законом Дюлонга–Пти. Для твердых тел практически не существует различия между C_p и C_V из-за ничтожно малой работы при расширении или сжатии.

Понятие квантовой теории теплоемкостей газов.

Для решения задачи о теплоемкости двухатомных газов необходимо воспользоваться формулами квантовой статистики. Вычислим статистическую сумму, полагая верхний предел для энергии равным

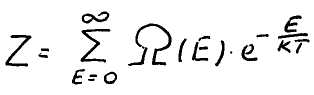
Энергию идеального газа можно представить как сумму энергии отдельных частиц, так как между ними нет взаимодействия. Статистическую сумму можно записать в виде

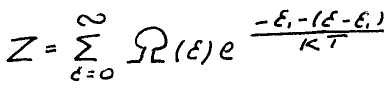
Это выражение после упрощения принимает вид

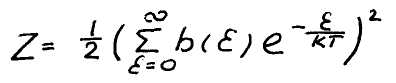
Теплоемкость газа определяется по формуле

Внутренняя энергия вычисляется через статистическую сумму

Она подставляет собой сумму энергий поступательного колебательного и вращательного движения частиц

Внутренняя энергия определяется следующими соотношениями

И теплоемкости представлены в виде суммы трех величин.

№11 Квазистатические процессы. Второе начало термодинамики. Основное термодинамическое тождество. Взаимопревращение внутренней и других форм энергии. Тепловые двигатели. Максимальное К.П.Д. тепловых двигателей.

Если в ходе термодинамического процесса система в каждый момент времени находится в равновесном состоянии, то процесс называется равновесным. В теоретической физике такие процессы называются квазистатическими, т.е. в каждый момент систему приближенно можно считать не изменяющейся, застывшей в равновесном состоянии. Процесс можно считать равновесным, если скорость изменения произвольного параметра в ходе процесса значительно меньше скорости изменения этого же параметра при релаксации: , – время релаксации (процесс перехода к равновесному состоянию называется релаксацией). Из определения следует, что квазистатическими можно считать процессы, протекающие медленно.

Внутренняя энергия является однозначной функцией состояния термодинамической системы, т.е. функцией внешних и внутренних параметров состояния, следовательно, изменения внутренней энергии определяются изменениями этих параметров.

Работа – любой способ передачи энергии, связанный с изменением внешних параметров системы. Можно сказать, что работа – количество переданной энергии.

Для равновесных процессов работу можно записать в виде: , где – внешний параметр, – сопряженная ему обобщенная сила. При равновесном адиабатическом переходе из состояния в состояние изменение внутренней энергии равно: , т.к. , то обобщенная сила равна: . Из этого выражения следует, что обобщенная сила является функцией температуры и внешних параметров системы.

При одновременном изменении внешних нескольких параметров работа равна: .

Изменение внутренней энергии термодинамической системы необязательно сопряжено с изменением внешних параметров.

Теплопередача (теплообмен) – процесс передачи энергии при постоянных внешних параметрах, т.е. без совершения работы.

Количество переданной энергии называется количеством теплоты.

, где С – теплоемкость системы.

Выводы:

Работа и теплота это способы перехода энергии от одной системы к другой.

Работа и теплота это характеристики совершаемого процесса, а не состояния системы.