
- •Длина пути s пройденного точкой за промежуток времени от t1 до t2 задается интегралом
- •Законы Ньютона.
- •И.С.О. Энергия. Работа. Кинетическая и потенциальная энергия. Закон сохранения энергии. Границы применимости з.С.Э.
- •1.2 Добротностью колебательной системы называется безразмерная величина q, равная произведению 2 на отношение энергий
- •Экспериментальные основы с.Т.О. Постулаты Эйнштейна. Пространство время и системы отсчета в с.Т.О. Преобразование Лоренца и их кинематические следствия.
- •Второй закон термодинамики.
- •1 . Поле бесконечной однороно заряженной плоскости. Рассмотрим поле создаваемое бесконечной плоскостью заряженной положительно с постоянной поверхностной плотностью .
- •2. Магнитное поле в центре кругового тока.
- •Энергия магнитного поля
- •Принцип соответствия Бора: выводы и законы квантовой механики при больших значениях квантовых чисел должны соответствовать выводам и законам классической физики.
- •Фермионы и бозоны.
1.2 Добротностью колебательной системы называется безразмерная величина q, равная произведению 2 на отношение энергий
![]()
W(t)- энергия в произвольный момент времени t
W(t+T) - убыль энергия за промежуток времени t+T
![]()
Где θ - логарифмический декремент затухания
Резонанс – явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к чистоте близкой собственной частоте колебаний.

![]()
При
частоте ![]()
Гармонический
осциллятор — это система, которая при
смещении из положения равновесия
испытывает действие возвращающей силы,
пропорциональной смещению (согласно
закону Гука):
![]() .
где k — положительная константа,
описывающая жёсткость системы. Если –
единственная сила, действующая на
систему, то систему называют простым
или консервативным гармоническим
осциллятором. Свободные колебания такой
системы представляют собой периодическое
движение около положения равновесия
(гармонические колебания). Частота и
амплитуда при этом постоянны, причём
частота не зависит от амплитуды. Если
имеется ещё и сила трения (затухание),
пропорциональная скорости движения,
то такую систему называют затухающим
осциллятором. Если трение не слишком
велико, то система совершает почти
периодическое движение. Если осциллятор
предоставлен сам себе, то говорят, что
он совершает свободные колебания. Если
же присутствует внешняя сила, то говорят,
что осциллятор испытывает вынужденные
колебания. Механическими примерами
гармонического осциллятора являются
математический маятник, груз на пружине.
В качестве модели гармонического
осциллятора возьмём груз массы,
закреплённый на пружине жёсткостью.
Пусть x
– это смещение
груза относительно положения равновесия.
Тогда, согласно закону Гука, на него
будет действовать возвращающая сила:
.
Используя второй закон Ньютона,
запишем:
.
где k — положительная константа,
описывающая жёсткость системы. Если –
единственная сила, действующая на
систему, то систему называют простым
или консервативным гармоническим
осциллятором. Свободные колебания такой
системы представляют собой периодическое
движение около положения равновесия
(гармонические колебания). Частота и
амплитуда при этом постоянны, причём
частота не зависит от амплитуды. Если
имеется ещё и сила трения (затухание),
пропорциональная скорости движения,
то такую систему называют затухающим
осциллятором. Если трение не слишком
велико, то система совершает почти
периодическое движение. Если осциллятор
предоставлен сам себе, то говорят, что
он совершает свободные колебания. Если
же присутствует внешняя сила, то говорят,
что осциллятор испытывает вынужденные
колебания. Механическими примерами
гармонического осциллятора являются
математический маятник, груз на пружине.
В качестве модели гармонического
осциллятора возьмём груз массы,
закреплённый на пружине жёсткостью.
Пусть x
– это смещение
груза относительно положения равновесия.
Тогда, согласно закону Гука, на него
будет действовать возвращающая сила:
.
Используя второй закон Ньютона,
запишем:![]() .
Обозначая
.
Обозначая
![]() и заменяя ускорение a
на вторую
производную от координаты по времени,
напишем:
и заменяя ускорение a
на вторую
производную от координаты по времени,
напишем:
![]() .
Это дифференциальное уравнение описывает
поведение гармонического осциллятора.
Коэффициент ω0
называют циклической частотой осциллятора.
Будем искать решение в виде:
.
Это дифференциальное уравнение описывает
поведение гармонического осциллятора.
Коэффициент ω0
называют циклической частотой осциллятора.
Будем искать решение в виде:
![]() .
.
Получаем
условие на частоту колебаний:
![]() ,
,![]() .
Отрицательную частоту можно отбросить,
так как произвол в выборе этого знака
покрывается произволом выбора начальной
фазы. Общее решение уравнения записывается
в виде:
.
Отрицательную частоту можно отбросить,
так как произвол в выборе этого знака
покрывается произволом выбора начальной
фазы. Общее решение уравнения записывается
в виде:
![]() ,
где амплитуда A и начальная фаза φ —
произвольные постоянные.
,
где амплитуда A и начальная фаза φ —
произвольные постоянные.
Кинетическая энергия записывается в виде:
![]()
и
потенциальная энергия есть:
![]()
тогда
полная энергия имеет постоянное значение:
![]()
№5 Гравитационное поле. Закон всемирного тяготения. Опыт Кавендиша. Инертная и гравитационная масса. Задача двух тел. Задача Кеплера.
Гравитационное взаимодействие между телами осуществляется посредством создаваемого ими гравитационного поля называемого также полем тяготения. Особенность гравитационного поля состоит в том, что на помещенную в него материальную точку действует сила пропорциональная массе этой точки.
Силовой
характеристикой гравитационного поля
служит его напряженность – векторная
величина ![]() равная отношению величины силы действующей
со стороны поля на помещенную в него
материальную точку, к массе m
этой точки
равная отношению величины силы действующей
со стороны поля на помещенную в него
материальную точку, к массе m
этой точки ![]() .
Напряженность гравитационного поля
не зависит от массы m
материальной точки, она является функцией
координат (x,y,z)
точек рассматриваемого поля .
.
Напряженность гравитационного поля
не зависит от массы m
материальной точки, она является функцией
координат (x,y,z)
точек рассматриваемого поля .
Закон
всемирного тяготения. Согласно этому
закону, сила с которой две материальные
точки притягивают друг друга,
пропорциональны массам этих точек и
обратно пропорциональна квадрату
расстояния между ними ![]() где G
– гравитационная постоянная. Эта сила
называется гравитационной или силой
всемирного тяготения.
где G
– гравитационная постоянная. Эта сила
называется гравитационной или силой
всемирного тяготения.
С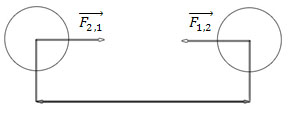
 илы
гравитационные – притяжения, центральные
т.к. направлены по линии соединяющие
центры материальных точек. Опыт
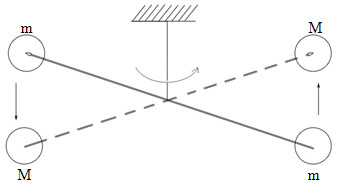
Кавендиша.
Первой успешной попыткой определение
G
были измерения, осуществленные Кавендишем.
Для измерения сил он применил чувствительный
метод крутильных весов. Два свинцовых
шара m?
прикрепленных к концам легкого коромысла,
помещались вблизи симметрично
расположенных шаров M.
Коромысло подвешивалось на упругой
нити, по закручиванию которой можно
было измерить силу притяжения шаров
друг к другу.
илы
гравитационные – притяжения, центральные
т.к. направлены по линии соединяющие
центры материальных точек. Опыт
Кавендиша.
Первой успешной попыткой определение
G
были измерения, осуществленные Кавендишем.
Для измерения сил он применил чувствительный
метод крутильных весов. Два свинцовых
шара m?
прикрепленных к концам легкого коромысла,
помещались вблизи симметрично
расположенных шаров M.
Коромысло подвешивалось на упругой
нити, по закручиванию которой можно
было измерить силу притяжения шаров
друг к другу. ![]() ;
Если подставить
;
Если подставить ![]() и
и ![]() ,
то сила окажется численно равна G.
F=
6.67* 10-11 H.
,
то сила окажется численно равна G.
F=
6.67* 10-11 H.
Инертная и гравитационная масса. Масса входит в двух различных законах: во втором законе Ньютона и в законе всемирного тяготения. В первом случае она характеризует инертные свойства тела, во втором гравитационные свойства, т.е. способность тел притягивать друг друга. Возникает проблема не следует ли различать инертную массу и массу гравитационную. Опытные факты указывают на то, что инертная и гравитационная масса всех тел строго пропорциональны друг другу. Это означает, что при строгом выборе единиц измерения гравитационная и инертная массы становятся тождественными, поэтому в физике говорят просто о массе. Простейший из этих опытов заключается в проверке, действительно ли все тела (из любых веществ) падают на Земле с одинаковым ускорением. Пусть мы имеем два разнородных тела, например из железа и гранита. Обозначим их инертные и гравитационные массы через m1ин, m1грав, и m2ин, m2грав. Для первого тела
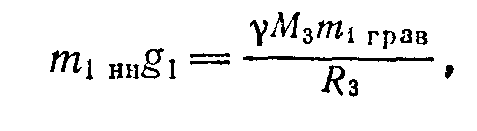 ,
(1)
,
(1)
А для второго
![]() (2)
(2)
После деления уравнения (1) на (2) получим
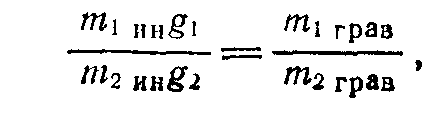 или
или
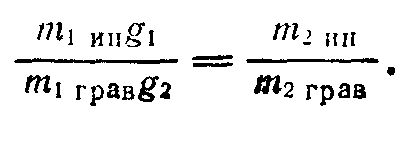
Полученное соотношение показывает, что отношение инертной массы тела к его гравитационной массе будет для всех тел (из любых веществ) одинаковым
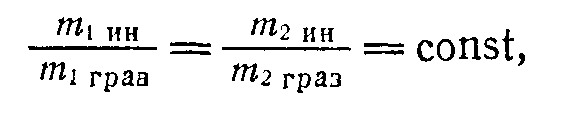
если будет доказано, что все тела независимо от их размера и рода вещества падают в вакууме с одинаковым ускорением. Опыты по непосредственному измерению ускорения свободного падения показывают, что это ускорение в пределах точности измерения одинаково для всех тел.
Тождественность гравитационной и инертной массы положена Эйнштейном в основу общей теории относительности.
З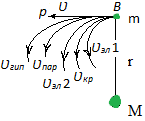 адача
двух тел. В
данном случае рассматривается движение
двух небесных тел под действием сил
всемирного тяготения, предположение,
что никакие другие тела на них не
действуют. В этом случае задачу называют
задачей двух тел. Если тела имеют
сравнимую массу, то оба тела совершают
движение вокруг общего центра масс.
Если масса одного тела значительно
превосходит массу другого, то такая
задача называется ограниченной задачей
двух тел. Предположим что тело массой
адача
двух тел. В
данном случае рассматривается движение
двух небесных тел под действием сил
всемирного тяготения, предположение,
что никакие другие тела на них не
действуют. В этом случае задачу называют
задачей двух тел. Если тела имеют
сравнимую массу, то оба тела совершают
движение вокруг общего центра масс.
Если масса одного тела значительно
превосходит массу другого, то такая
задача называется ограниченной задачей
двух тел. Предположим что тело массой
![]() находится на расстоянии
находится на расстоянии
![]() от тела массой
от тела массой![]() и движется со скоростью V,
тогда в зависимости от величины этой
скорости, расстояния до небесного тела,
движение может происходить различным
образом.
и движется со скоростью V,
тогда в зависимости от величины этой
скорости, расстояния до небесного тела,
движение может происходить различным
образом.
![]() ,
,![]() ,
,![]() -орбита
будет эллиптическая причем тело массой
M
будет лежать в дальнем фокусе эллипса.Если
-орбита
будет эллиптическая причем тело массой
M
будет лежать в дальнем фокусе эллипса.Если
![]() ,
,
![]() -
орбита будет опять эллиптической, тело
массой M
будет лежать в ближнем фокусе эллипса.
Если
-
орбита будет опять эллиптической, тело
массой M
будет лежать в ближнем фокусе эллипса.
Если
![]() -
параболическая скорость.Орбита будет
сильно вытянута и разорвана. Если
-
параболическая скорость.Орбита будет
сильно вытянута и разорвана. Если
![]() - скорость называется гиперболической
, тело будет двигаться по ветви гиперболы
и покинет поле тяготения Солнца. Если
скорость больше гипербалической , то
тело будет продолжать движение по прямой
вр. Если скорость равна 0, то тело будет
падать на тело массой M
по прямой вМ.
- скорость называется гиперболической
, тело будет двигаться по ветви гиперболы
и покинет поле тяготения Солнца. Если
скорость больше гипербалической , то
тело будет продолжать движение по прямой
вр. Если скорость равна 0, то тело будет
падать на тело массой M
по прямой вМ.
Т. о. под действием силы всемирного тяготения одно тело может двигаться в поле тяготения другого по одному из конических сечений: эллипсу, кругу, рараболе, гиперболе.
№6
