
- •Длина пути s пройденного точкой за промежуток времени от t1 до t2 задается интегралом
- •Законы Ньютона.
- •И.С.О. Энергия. Работа. Кинетическая и потенциальная энергия. Закон сохранения энергии. Границы применимости з.С.Э.
- •1.2 Добротностью колебательной системы называется безразмерная величина q, равная произведению 2 на отношение энергий
- •Экспериментальные основы с.Т.О. Постулаты Эйнштейна. Пространство время и системы отсчета в с.Т.О. Преобразование Лоренца и их кинематические следствия.
- •Второй закон термодинамики.
- •1 . Поле бесконечной однороно заряженной плоскости. Рассмотрим поле создаваемое бесконечной плоскостью заряженной положительно с постоянной поверхностной плотностью .
- •2. Магнитное поле в центре кругового тока.
- •Энергия магнитного поля
- •Принцип соответствия Бора: выводы и законы квантовой механики при больших значениях квантовых чисел должны соответствовать выводам и законам классической физики.
- •Фермионы и бозоны.
№1 Материальная точка. Уравнения движения материальной точки в векторной и координатной формах. Графики зависимости перемещения, скорости от времени. И.С.О. Законы Ньютона, границы их применимости. Принцип относительности Галилея.
Если линейными размерами тела можно пренебречь (тело во много раз меньше рассматриваемых расстояний) или структура тела не вносит в задачу изменений, а так же если вращение тела не вносит изменения в поступательный характер движения, то тело можно считать материальной точкой.
Для описания движения материальной точки прежде всего необходимо выбрать систему отсчета, т.е. координатную систему с часами для отсчета времени, связанную с каким-либо реальным телом.
Тело отсчета – произвольно выбранное тело относительно которого определяется положение других тел.
Система отсчета – совокупность системы координат и часов связанных с телом отсчета.
Наиболее
употребляемая система координат –
декартовая (базис ее образован тремя
единичными по модулю и взаимно
ортогональными векторами ![]() проведенными из начала координат)
проведенными из начала координат)
Линия в пространстве, вдоль которой перемещается материальная точка называется траекторией.
 Движение
материальной точки определенно, если
декартовы координаты материальной
точки заданы в зависимости от времени
Движение
материальной точки определенно, если
декартовы координаты материальной
точки заданы в зависимости от времени
![]() (1)
(1)
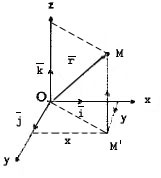
Положение
материальной точки M
характеризуется радиус-вектором ![]() соединяющим начало координат O
с точкой M.
соединяющим начало координат O
с точкой M.
![]()
![]() (2)
(2)
Это
кинематическое уравнение движения
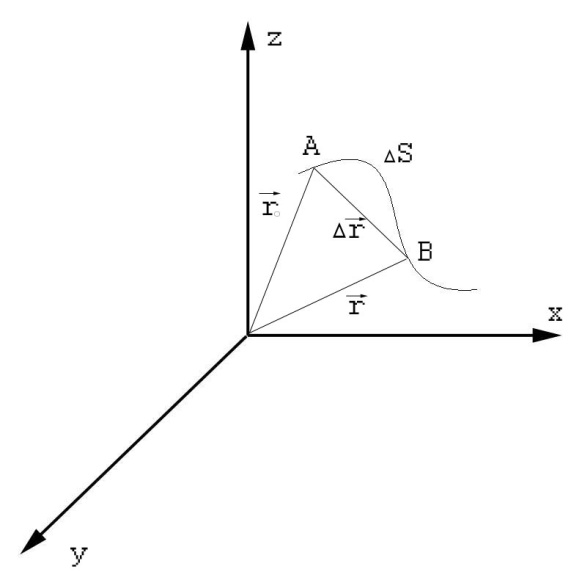
точки. Вектор перемещения ![]() - вектор, проведенный из начального
положения движущейся точки в положение
ее в данный момент времени.
- вектор, проведенный из начального
положения движущейся точки в положение
ее в данный момент времени.
![]()
Длиной
пути точки ![]() называется сумма длин всех участков
траектории, пройденных точкой за
промежуток времени
называется сумма длин всех участков
траектории, пройденных точкой за
промежуток времени ![]() .
Длина пути – скалярная величина. Скорость
– это векторная величина, определяющая
как быстроту движения тел, так и его
направление в данный момент времени.
Вектором средней скорости за промежуток
времени
.
Длина пути – скалярная величина. Скорость
– это векторная величина, определяющая
как быстроту движения тел, так и его
направление в данный момент времени.
Вектором средней скорости за промежуток
времени ![]() называется отношение приращение
радиусветора
называется отношение приращение
радиусветора ![]() точки к промежутку времени
.
точки к промежутку времени
.
![]()
![]()
Мгновенная
скорость – векторная величина, равная
первой производной по времени от
радиус-вектора ![]() рассматриваемой точки.
рассматриваемой точки.
![]()
Вектор мгновенной скорости направлен по касательной к траектории в сторону движения. Модуль мгновенной скорости (скалярная величина) равен
![]()
Длина пути s пройденного точкой за промежуток времени от t1 до t2 задается интегралом
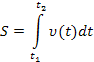
Ускорение- это векторная величина характеризующая быстроту изменения скорости по модулю и направлению.
Ускорение точки- векторная величина, равная первой производной по времени скорости рассматриваемой точки.
![]() ;
;
![]()
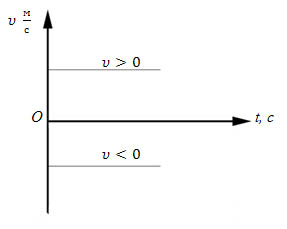
Графики
строятся для скалярных величин запишем
уравнение ![]()
А)
Равномерное прямолинейное движение
![]() ;
равноускоренное прямолинейное
движение
;
равноускоренное прямолинейное
движение![]()
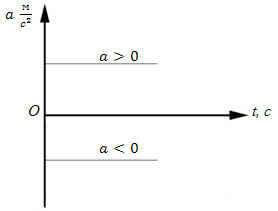
Равноускоренное прямолинейное движение.
![]()
![]() ;
;
![]()
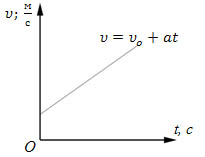
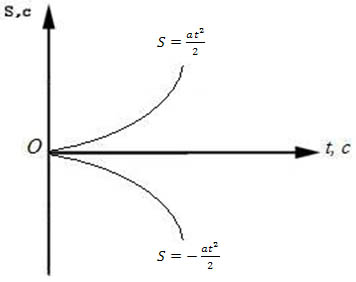
Системы отсчета, в которых тело, не подверженное действию других тел, движется равномерно прямолинейно(или покоится), принято называть инерциальными системами.
Законы Ньютона.
Первый закон Ньютона постулирует существование инерциальных систем отсчета – таких относительно которых материальная точка, не подвержена воздействию других тел, движется равномерно и прямолинейно.
Первый закон Ньютона – материальная точка (тело) сохраняет состояние покоя и равномерного прямолинейного движения до тех пор пока воздействие со стороны других тел не заставит ее изменить это состояние. Стремление тел сохранять состояние покоя или равномерного прямолинейного движения называется инерцией. Поэтому первый закон называют законом инерции.
Второй закон Ньютона. Ускорение, приобретаемое материальной точкой (телом) пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точка (тела) :
![]() или
или ![]()
Векторная
величина ![]() - называется импульса силы,
- называется импульса силы, ![]() или
или
![]()
Третий
закон Ньютона. Всякое действие материальных
точек (тел) друг на друга имеет характер
взаимодействия; силы с которыми
материальные точки действуют друг на
друга равны по модулю, противоположно
направлены и действуют вдоль прямой,
соединяющей эти точки. ![]()
Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.
В классической механике ,при скоростях тел значительно меньших чем скорость света справедлив механический принцип относительности (Принцип относительности Галилея) : законы механики одинаковы во всех инерциальных системах отсчета, при одинаковых начальных условиях.
Р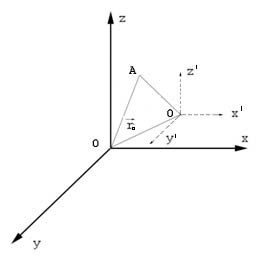 ассмотрим
две системы отсчета И.С.О. K
(координаты x,y,z)
неподвижную и И.С.О. K’
– движущуюся
относительно K
равномерно и прямолинейно
ассмотрим
две системы отсчета И.С.О. K
(координаты x,y,z)
неподвижную и И.С.О. K’
– движущуюся
относительно K
равномерно и прямолинейно ![]()
В
начальный момент t=0
начала координат O
и O’
этих систем
совпадают. В произвольный момент времени
t
:
![]()
![]()
Для произвольной точки A
![]() В проекциях
на оси координат
В проекциях
на оси координат
![]() ;
y
;
y![]() ;
;
![]() .
.
Эти соотношения называются преобразованиями Галилея.
№2 Инерциальные системы отсчета. Механическая система. Замкнутые механические системы. Импульс(материальной точки системы). Закон сохранения импульса. Момент импульса(материальной точки, твердого тела, механической системы). Закон сохранения момента импульса. Границы применимости закона сохранения момента импульса.
Системы отсчета, в которых тело, не подверженное действию других тел, движется равномерно прямолинейно(или покоится), принято называть инерциальными системами.
Механической системой называется совокупность материальных точек (тел) рассматриваемых как единое целое.
Тела не входящие в состав исследуемой механической системы называются внешними телами. Силы, действующие на систему со стороны других внешних тел, называются внешними силами.
Внутренними силами называются силы между частями рассматриваемой системы.
Механическая система называется замкнутой, или изолированной системой, если она не взаимодействует с внешними телами (на нее не действуют внешние силы, или действием внешних сил можно пренебречь).
Импульсом
материальной точки называют векторную
величину ![]() равную произведению массы точки на ее
скорость
равную произведению массы точки на ее
скорость ![]() [p]=
кг*м/с
[p]=
кг*м/с
Воспользовавшись
определением импульса, уравнение второго
закона Ньютона можно записать в виде
![]() производная импульса, материальной
точки по времени равна равнодействующей
всех сил, действующих на точку.
производная импульса, материальной
точки по времени равна равнодействующей
всех сил, действующих на точку.
Рассмотрим замкнутую систему, состоящую из N материальных точек (систем тел). Импульсом системы называется векторная сумма импульсов тел образующих систему:
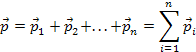
Назовем
центром инерции системы точку, положение
которой в пространстве задается радиусом
вектором ![]() определяемым следующим образом.
определяемым следующим образом.
![]()
Где
![]() - масса i-
ого тела,
- масса i-
ого тела, ![]() - результирующий вектор, определяющий
положение этого тела в пространстве, m
- масса системы.
- результирующий вектор, определяющий
положение этого тела в пространстве, m
- масса системы.
Отметим, что центр инерции совпадает с центром тяжести системы (частный случай в однородном поле силы тяжести).
Скорость
центра инерции получается путем
дифференцирования ![]() по
времени:
по
времени:
![]()
Учитывая,
что ![]() есть
импульс а
есть
импульс а ![]() дает
импульс системы , можно записать
дает
импульс системы , можно записать
![]() (1)
(1)
Таким образом импульс системы равен произведению массы системы на скорость ее центра инерции.
Рассмотрим систему, состоящую из произвольного числа тел N. Пользуясь сокращенной записью сумм, уравнение (1) для всех N тел можно представить следующим образом:
![]() (i=1,2,…,n)
(2)
(i=1,2,…,n)
(2)
Выражение
(2) представляет собой систему N
уравнений, отличающихся друг от друга
значением индекса i.
Суммирование в каждом из этих уравнений
производится по индексу k
(![]() ).
Складывая уравнения, с учетом того что
).
Складывая уравнения, с учетом того что
![]() получим
получим
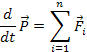
Производится
по времени от вектора импульса системы
равна векторной сумме внешних сил,
приложенных к телам системы для замкнутой
системы ![]() , поэтому
, поэтому ![]() не зависит от времени. Закон сохранения
импульса формулируется так: импульс
замкнутой системы материальных точек
остается постоянным. Закон сохранения
импульса принадлежит к числу основных
законов.
не зависит от времени. Закон сохранения
импульса формулируется так: импульс
замкнутой системы материальных точек
остается постоянным. Закон сохранения
импульса принадлежит к числу основных
законов.
Для характеристики внешнего механического действия на тело (поступательного и вращательного) вводится понятие момента импульса.
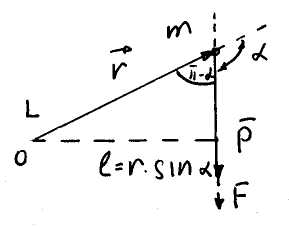 Момент
импульса (момент количества движения)
материальной точки относительно
неподвижной точки О (полюса) L
равен векторному произведению радиуса
– вектора r,
проведенного из полюса O
в место нахождения материальной точки,
на вектор p
ее импульса.
Момент
импульса (момент количества движения)
материальной точки относительно
неподвижной точки О (полюса) L
равен векторному произведению радиуса
– вектора r,
проведенного из полюса O
в место нахождения материальной точки,
на вектор p
ее импульса.
![]()
Где m и υ – масса и скорость м. т.
![]() -
плечо
-
плечо
Модуль вектора момента импульса
![]()
Момент импульса материальной точки относительно оси Z называется составляющая Lz по этой оси момент импульса L относительно точки О.
![]()
Момент импульса системы относительно неподвижной точки O называется геометрическая сумма L моментов импульса относительно той же точки O. Всех материальных точек системы:
![]()
n- Общее число точек системы
Моментом импульса системы относительно неподвижной оси Z называется величина Lz равная проекции на эту ось вектора L момента импульса системы относительно какой либо точи J, принадлежащей этой оси:
![]()
Закон сохранения момента импульса.
Рассмотрим
систему из N
материальных точек. Результирующий
момент внутренних сил, действующих на
i-ую
материальную точку, обозначим ![]() ,
а внешних сил
,
а внешних сил ![]() запишем уравнение
запишем уравнение
![]()
(i=1,2,…,N) Это выражение имеет вид:
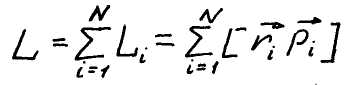
Момент импульса системы материальных точек. Сумма моментов внутренних сил равна нулю.
Обозначим суммарный момент внешних сил символом M запишем
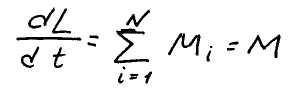
Для замкнутой системы материальных точек M=0, поэтому L=const - закон сохранения момента импульса. Момент импульса замкнутой системы материальных точек величина постоянная.
Закон сохранения момента импульса выходит за рамки классической механики. Он принадлежит к числу фундаментальных законов физики. Он связан с определенным свойством симметрии пространства – его изотропность. Изотропность пространства прояляется в том, что физические свойства и законы движения замкнутой системы не зависят от выбора осей координат И.С.О. т.е. не изменяются при повороте в пространстве замкнутой системы как целого на любой угол.
№3
