3.2. Пример расчета балки на прочность и жесткость

Требуется из расчета на прочность определить размеры поперечного сечения балки (рис. 3.3) в двух вариантах: "а" (рис. 3.4) и "б" (рис. 3.5), а затем проверить балку, имеющую поперечное сечение "а", на жесткость.

Принять:

М = 20 кНм; q = 20 кН/м;

F = 50 кН; R =200 МПа; R_s=120 МПа;

б_s=240 МПа; k = 1,2 (коэффициент запаса прочности).

Расчет балки на прочность.

Определение реакций опор.

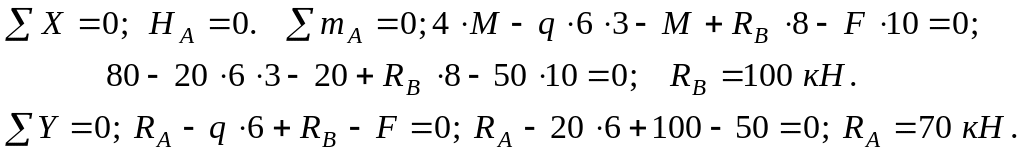Проверка:

(Верно)

Построение эпюр Q_y, M_z.

Балка имеет четыре грузовых участка.

1 грузовой участок: .

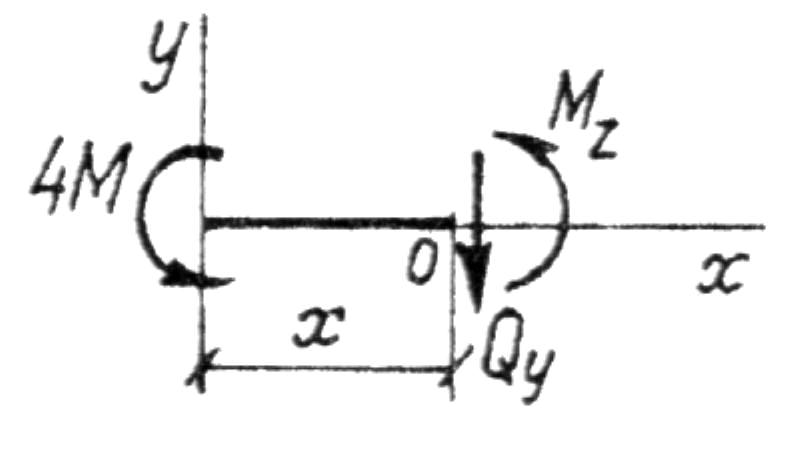
2 грузовой участок:

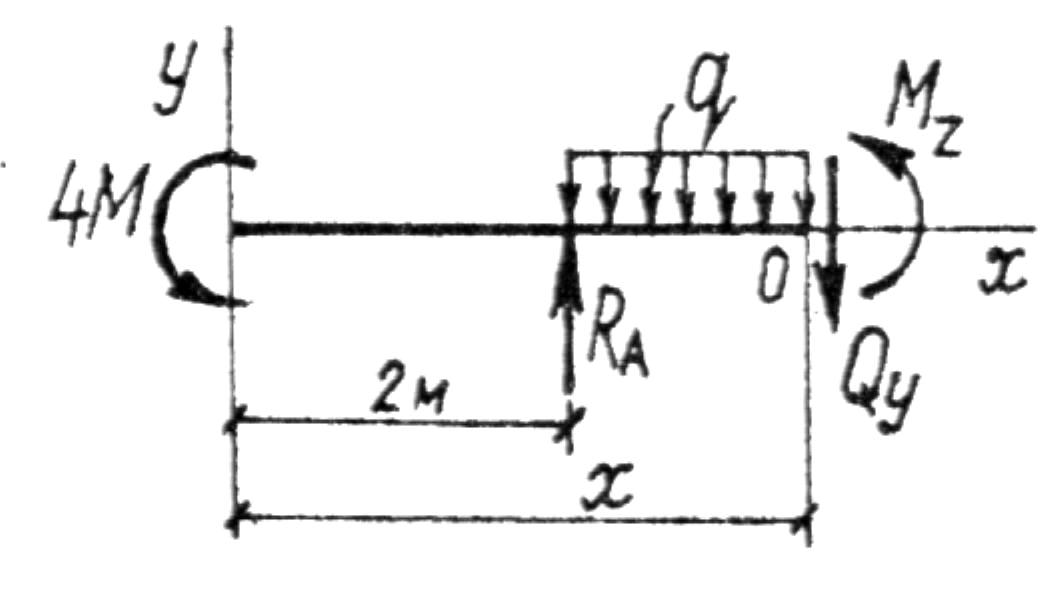
х = 2 м, Q_y = 70 кН;

х = 8 м, Q_y = – 50 кН

(т.к. Q_y на участке меняет знак, то M_z – имеет экстремум)

Найдём положение экстремума.

x = 5,5 м.

х = 2 м, M_z = – 80 кНм;

х = 5,5 м, M_z = 42,5 кНм;

х = 8 м, M_z = –20 кНм.

Для грузовых участков 3 и 4 вычисление M_z и Q_y выполнять аналогично, рассматривая правую отсеченную часть балки.

Эпюры Q_y и M_z показаны на рис. 3.3.

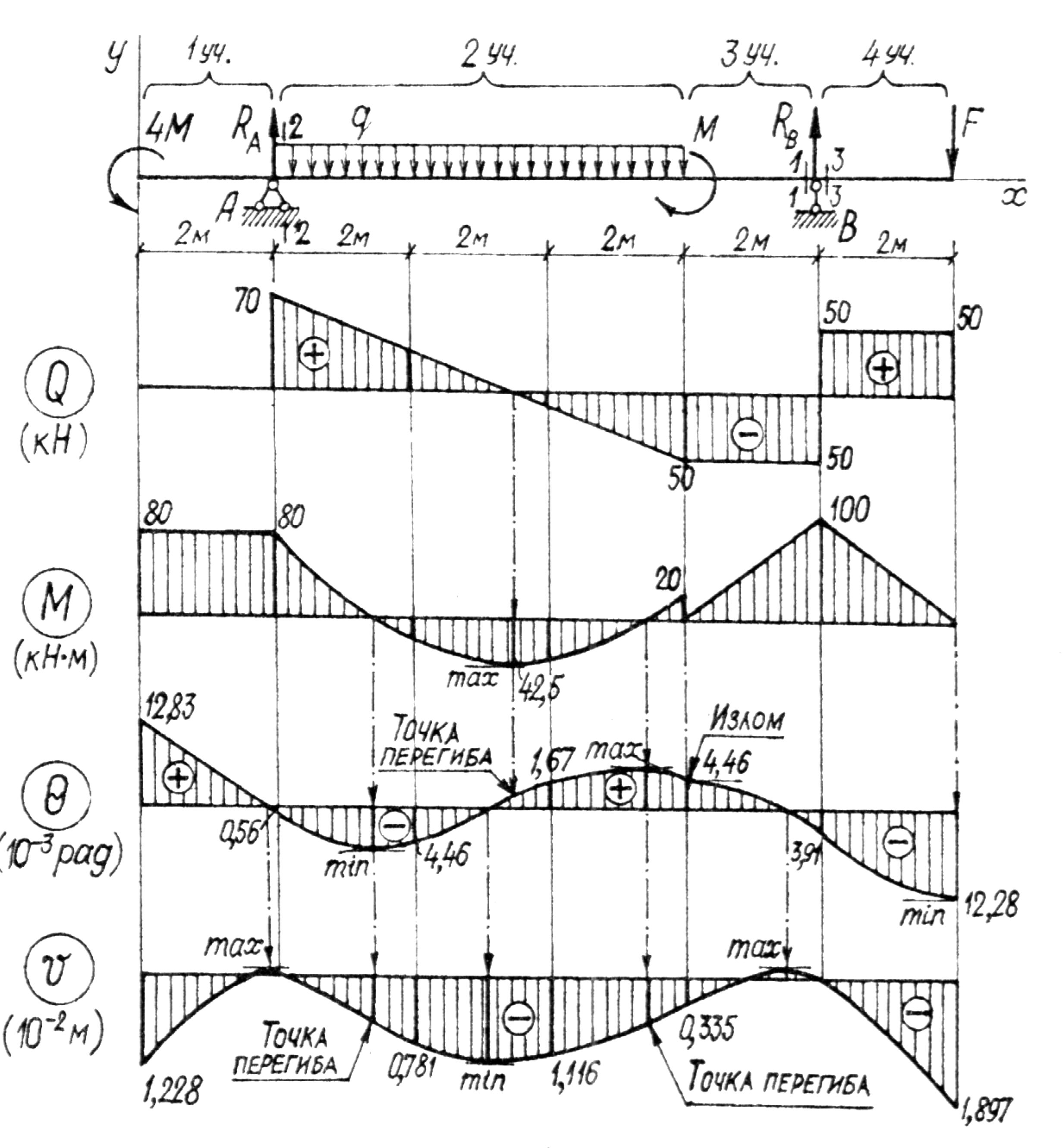
Рис. 3.3

Определение положения опасных сечений.

1-е опасное сечение: кНм;

2-е опасное сечение: кН;

3-е опасное сечение: M_z = – 100 кНм; Q_y = 50 кH.

Определение размеров поперечных сечений балки.

Из условия прочности по нормальным напряжениям в опасных точках D (рис. 3.4, 3.5) 1-го опасного сечения определим требуемый момент сопротивления:

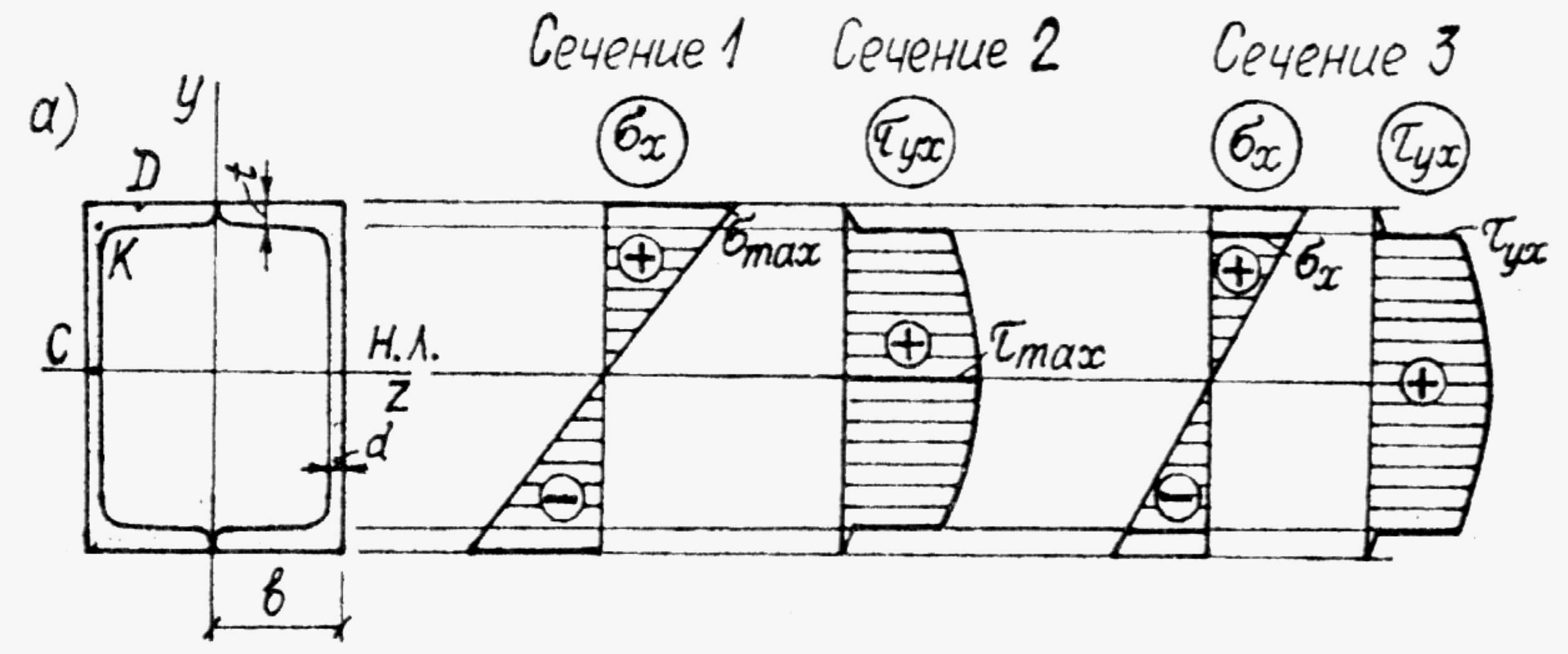
Рис. 3.4

Поперечное сечение варианта "а" (рис. 3.1), состоит из двух швеллеров. Для одного швеллера W_z =

По ГОСТ 8240-89 находим: [N 24, W_z = 242 см³;

2 [N 24, W_z = 484 см³.

Проверяем прочность принятого сечения по нормальным напряжениям:

Перенапряжение

что допустимо.

Проверка прочности по касательным напряжениям в опасной точке С (рис. 3.4) 2-го опасного сечения (чистый сдвиг):

Значение S_z для точки С, расположенной на нейтральной оси, берем из того же ГОСТа 8240-89.

Проверка прочности в опасной точке К (рис. 3.4) 3-го опасного сечения, где имеет место плоское напряжённое состояние:

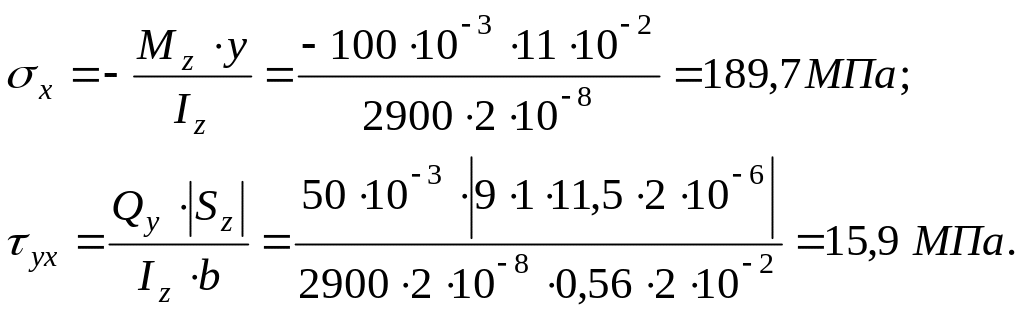
По гипотезе прочности наибольших касательных напряжений имеем: . Для балки при прямом поперечном изгибе получим:

По энергетической гипотезе прочности имеем:

Следовательно, прочность материала балки во всех точках обеспечена.

Рассмотрим расчет сварной балки – вариант "б" (рис. 3.1) с поперечным сечением, показанным на рис. 3.5.

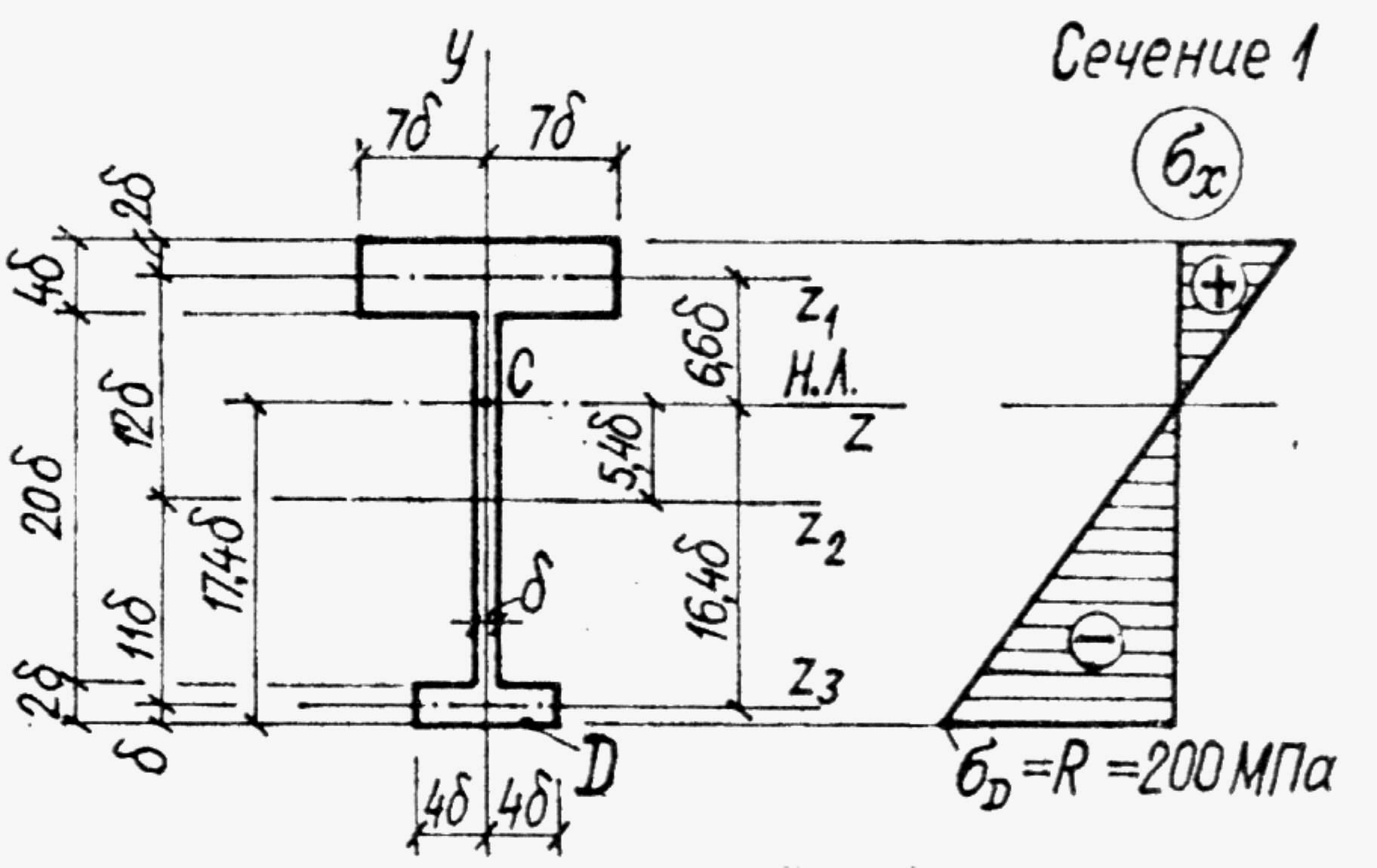
Рис. 3.5

Определим положение центра тяжести сечения:

Вычислим момент инерции:

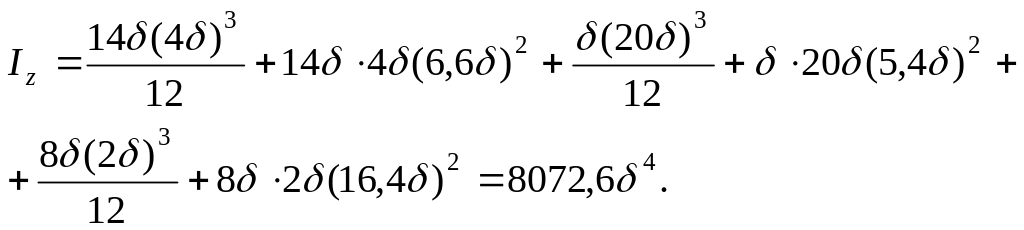
Момент сопротивления .

Из условия прочности по нормальным напряжениям в опасной точке D (рис. 3.5) 1-го опасного сечения получим:

464,2 ³ = 500 (см. с. 26). Отсюда .

В соответствии с найденной величиной принимаем размеры поперечного сечения с округлением до 1 мм (рис. 3.6). Пересчитав характеристики сечения, получим: I_z = 9017,6 см⁴.

W_z = 503,8 см³. Напряжение σ_max = 198,5 МПа < R. = 200 МПа.

Проверка прочности по касательным напряжениям в опасной точке С (рис. 3.6) 2-го опасного сечения:

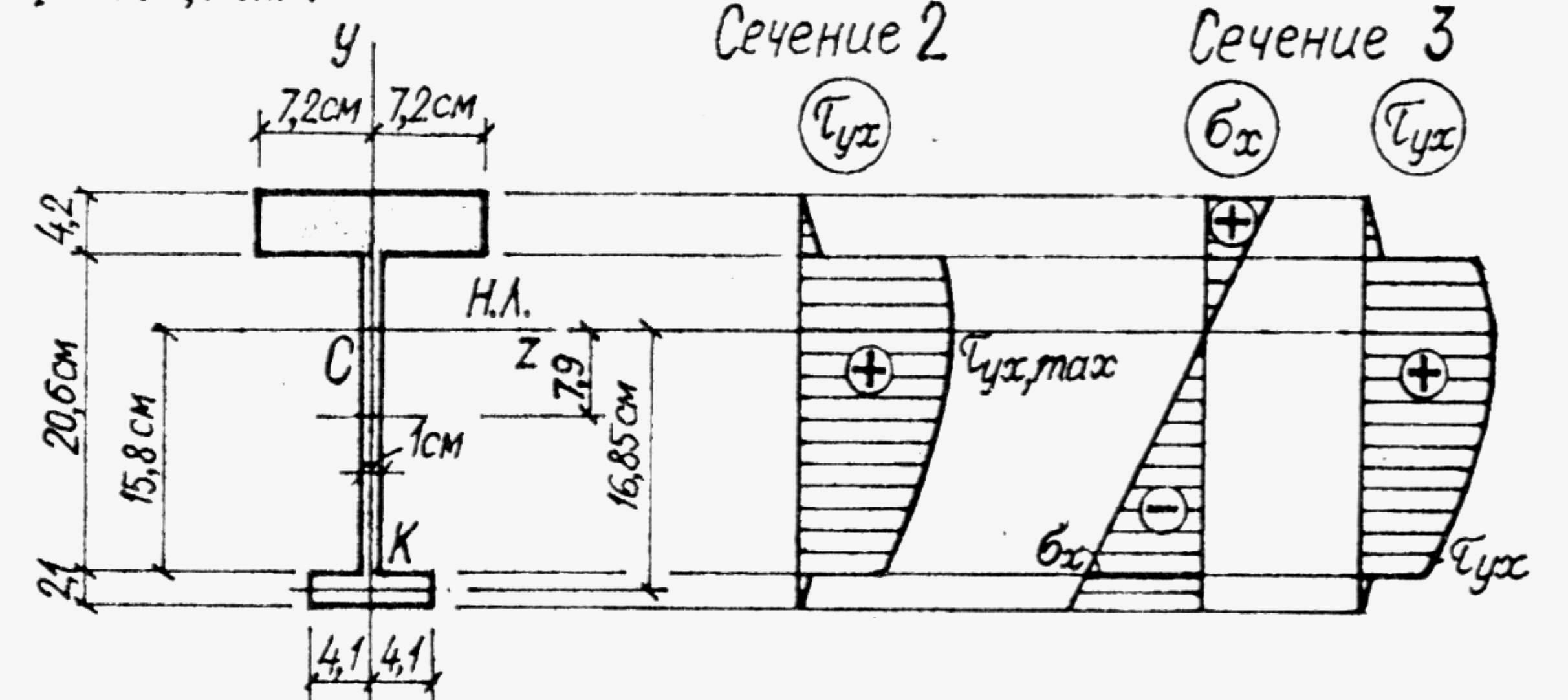
Рис. 3.6

т.е. условие прочности в точке С выполнено.

Проверка прочности в опасной точке К (рис. 3.6) 3-го опасного сечения, где имеет место плоское напряженное состояние:

По гипотезе прочности наибольших касательных напряжений имеем:

По энергетической теории прочности получим:

Условие прочности в точке К выполнено.

Расчет по предельной несущей способности (поперечное сечение приведено на рис. 3.7).

Дано: =240 МПа; k=1,2.

Определить размер .

Площадь поперечного сечения равна

Нейтральная ось Z₁ не проходит через центр тяжести сечения и делит площадь поперечного сечения А на две равновеликие площади:

Предельный момент в пластическом шарнире имеет выражение:

Пластический момент сопротивления

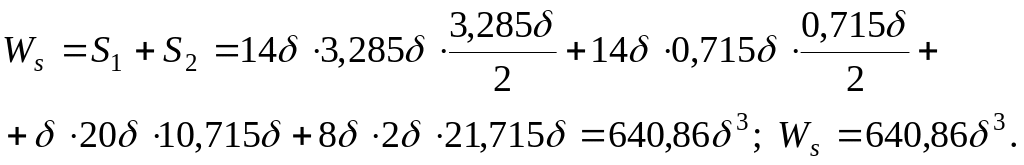
Из условия прочности

.

Сопоставив результаты расчетов методами расчетного сопротивления ( =1,025 см) и предельной несущей способности ( =0,920 см), видим, что более экономичное сечение получается при расчете методом предельного равновесия.

Расчет балки на жесткость методом начальных параметров

Рассчитывается балка (рис. 3.3), выполненная из двух швеллеров №24 по ГОСТ 8240-89. Жесткость сечения балки при изгибе

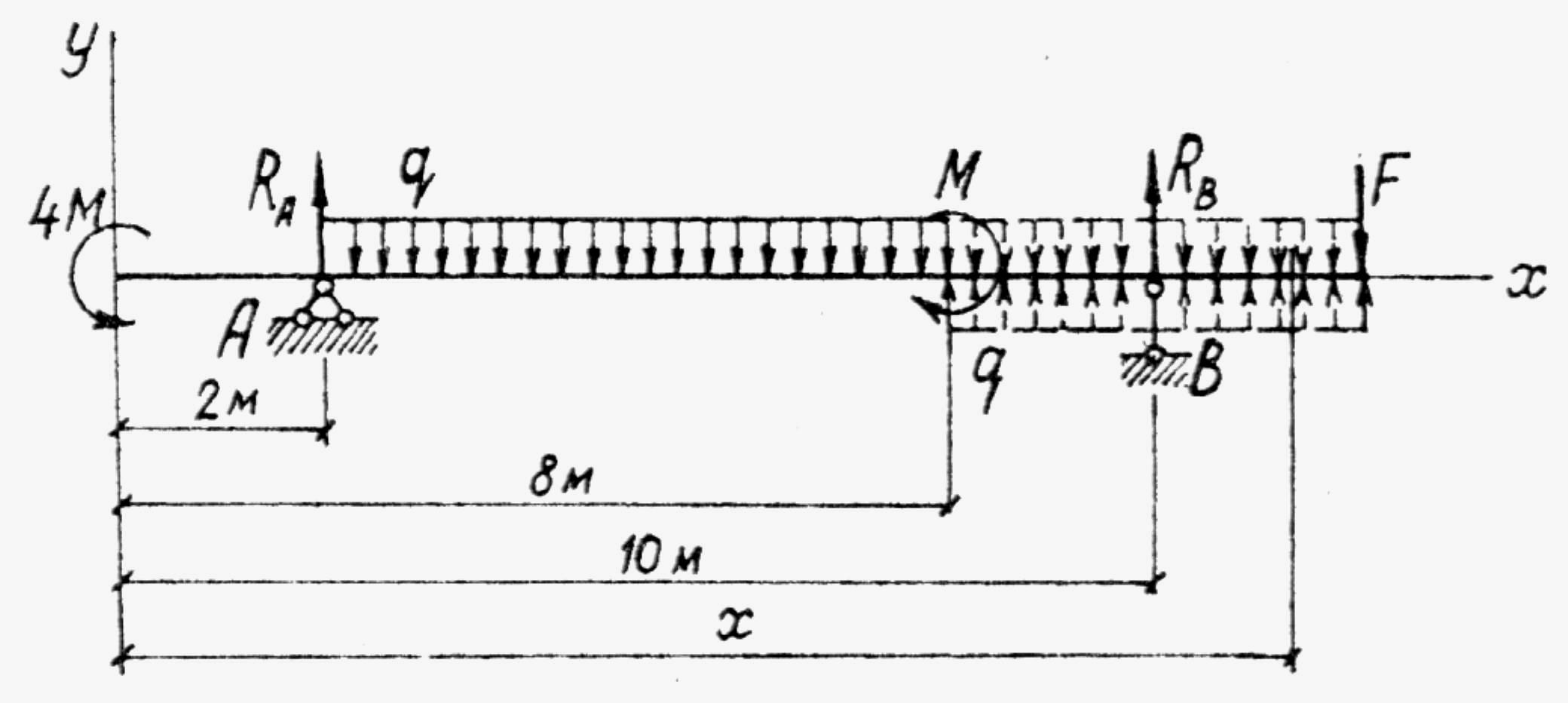
Рис. 3.8

Уравнения метода начальных параметров (2.4) и (2.5) для заданной балки (рис. 3.8) имеют вид:

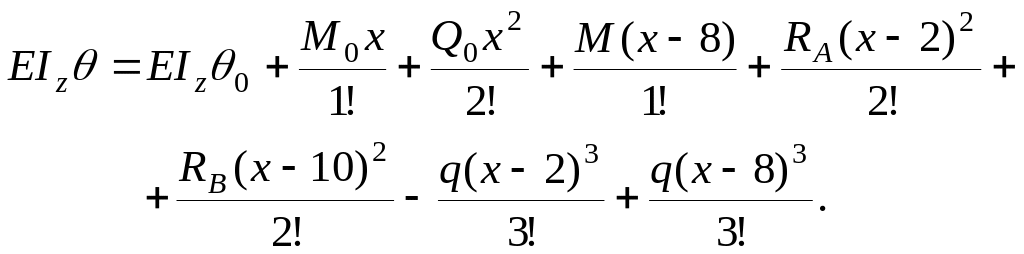
О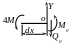 пределение начальных параметров.

Из условия равновесия элемента на

левом конце балки находим:

M₀ = – 4M; Q₀ = 0.

Кинематические граничные условия имеют вид:

1) x = 2 м, = 0; 2) х = 10 м, = 0.

Используя первое условие, получим

.

Используя второе условие, будем иметь:

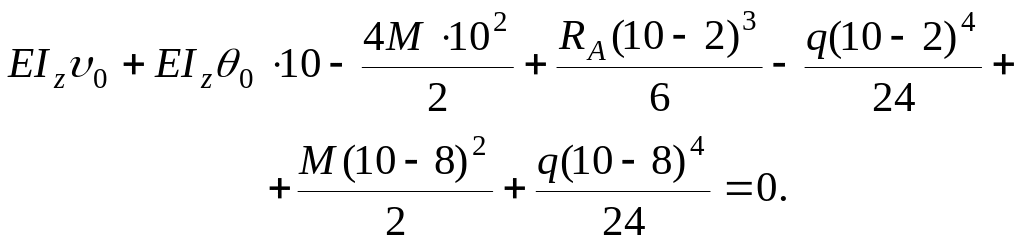
Решая полученную систему уравнений, находим:

Определим прогиб сечения на расстоянии х = 3 а = 6 м

и угол поворота сечения на расстоянии х = 6а = 12 м от начала координат

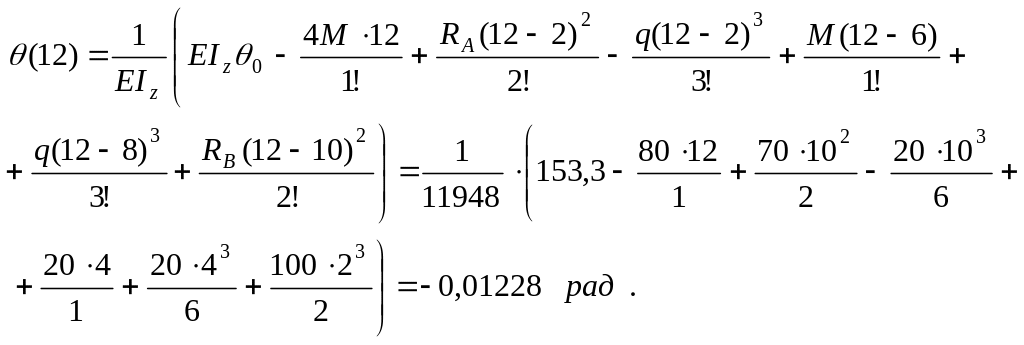
Аналогично можно найти прогибы и углы поворота других сечений и по полученным данным построить эпюры и . Дальнейшие расчеты выполняются с применением ЭВМ.

Исходные данные для расчета на ЭВМ по программе "IZGIB"

SH 312 – номер группы и варианта нагрузки;

L 12 – длина балки (м);

EI_z 11948 – жесткость сечения балки ;

N 6 – число равных отрезков, на которые разбита

балка;

NO 2 – число опор;

ПО 0 – условие закрепления балки в начале координат:

0 – свободный конец, 1 – шарнирная опора,

2 – защемление;

ПN 0 – условие закрепления балки на конце, противо-

положном началу координат;

L(i),D(i) 2, 0 – первая цифра – расстояние от начала координат

10, 0 до опоры, вторая – податливость опоры;

F_x 0 – продольная сила;

NM 2 – количество сосредоточенных моментов;

NF 1 – количество сосредоточенных сил, не считая

реакций опор;

NQ 2 – количество равномерно распределенных нагру-

зок, учитывая разгружающие нагрузки;

AM, M 0, –80 – расстояние от начала координат до точки при-

8, +20 ложения сосредоточенного момента, знак и ве-

личина момента. М>0, если растягивает ниж-

ние волокна;

AF, F 12, –50 – расстояние от начала координат до точки при-

ложения сосредоточенной силы, знак и вели-

чина сосредоточенной силы. F>0, если создает

момент, растягивающий нижние волокна;

AQ, Q 2, –20 – расстояние от начала координат до распреде-

8, +20 ленной нагрузки, знак и величина распределенной нагрузки; интенсивность q > 0, если создает момент, растягивающий нижние волокна.

OM 1 – расчет на прямой поперечный изгиб.

ШИФР 312

Результаты расчета по программе "IZGIB"

Начальные параметры

Реакции опор (кН)

R(1) = 70.00

R(2) = 100.00

Таблица 2

№ сечений	Коор­динаты сечений х (м)	Прогибы (м)	Углы поворота сечений (рад)	Изгиба­ющие моменты М ( )	Попе­речные силы Q (кН)
0	0.000	-.01228	.01283	-80.00	.00
1	2.000	.00000	-.00056	-80.00	.00
2	2.000	.00000	-.00056	-80.00	70.00
3	4.000	-.00781	-.00446	20.00	30.00
4	6.000	-.01116	.00167	40.00	-10.00
5	8.000	-.00335	.00446	-20.00	-50.00
6	8.000	-.00335	.00446	.00	-50.00
7	10.000	.00000	-.00391	-100.00	-50.00
8	10.000	.00000	-.00391	-100.00	50.00
9	12.000	-.01897	-.01228	.00	50.00

По результатам расчета на ЭВМ, приведенным в табл. 2, построены эпюры прогибов и углов поворота (рис. 3.3).

Проверим выполнение условия жесткости , где допускаемый прогиб =(1/400)l = 8/400 = 0,020 м.

Максимальный по модулю прогиб определяем по эпюре прогибов (рис. 3.3):

.

Условие жесткости 0,01897 м < 0,020 м выполняется.