4. Построение эпюр внутренних усилий в плоских стержнях с ломаной осью и при наличии криволинейных участков

Будем полагать, что стержень не является прямым, а его продольная ось располагается в плоскости Х,Y глобальной системы координат. В той же плоскости располагаются оси Х_i, Y_i локальных систем координат, относящиеся к отдельным участкам стержня, а также оси , относящиеся к любому поперечному сечению.

В случае рассмотрения равновесия произвольного плоского стержня тождество не выполняется, и из (1.2) следует, что силы внутреннего взаимодействия в сечении стержня суммируются к трем внутренним усилиям - изгибающему моменту М , поперечной силе Q и продольной силе N. В дальнейшем при рассмотрении плоского стержня индексы в обозначениях внутренних усилий опускаем.

Эпюры М, Q, N строятся по общим правилам, с использованием метода сечений. При выявлении зависимостей для усилий на грузовых участках можно использовать как глобальную, так и локальные системы координат. В частности, «нижние», т.е. расположенные со стороны соответствующей отрицательной полуоси Y_i (или ), волокна определяются в каждом сечении выбором локальных систем координат Х_i, Y_i, Z_i для участков (или , , – для отдельных сечений) по ранее описанной методике. Общий порядок построения эпюр М, Q, N описан в параграфе 1.4.

1. Примеры расчета.

ПРИМЕР 1

Для ломаного консольного стержня, изображенного на рис. 2.16 требуется построить эпюры M, Q, N.

РЕШЕНИЕ.

1.Опорные реакции в защемлении можно не определять, т.к. есть возможность при определении внутренних усилий всех сечениях рассматривать часть стержня со стороны свободного края консоли

2. Для построения эпюр выбираем сечения в начале и в конце каждого грузового участка, а там, где имеется распределенная нагрузка, дополнительно рассматриваем средние сечения участков.

3. В выбранных сечениях 1-1, 2-2,…..,9-9, , определяем внутренние усилия, используя приведенные ранее рабочие правила и рассматривая каждый раз свободную часть консоли.

. Продольные силы:

N_1-1=N_2-2=0; N_3-3 = N_4-4 = N_5-5= –30 кН;

N_6-6= N_7-7 = –q∙2 = –20 кН;

N_8-8 = N_9-9 = –q∙2 = –20 кН.

Поперечные силы:

Q_1-1=Q_2-2=0; Q_3-3 = 0;

Q_5-5 = q∙2 = 20 кН; Q_6-6 = Q_7-7 = –q∙2 = –20 кН;

Q_8-8 = Q_9-9 = –F₁+F₂ = –30+40 = 10 кН.

Рис. 2.16.

г) Проверка равновесия узла С

Рис. 2.17.

Изгибающие моменты:

М_1-1= М_2-2 = 12 кН∙м (растягиваются нижние волокна);

М_3-3 = М=12 кН∙м (растягиваются правые волокна);

М_4-4 =М+q∙1∙0,5 = 17 кН∙м (растягиваются правые волокна);

М_5-5 = М+ q∙2∙1 =12 + 20 = 32 кН∙м (растягиваются правые вол.).

М_6-6 = –М–q∙2∙1=–12–20 = –32 кН∙м (растягив. верхние волокна);

М_7-7 = –М–q∙2∙1+F₁∙0,5= –12–20+30∙0,5= –17 кН∙м (растягиваются верхние волокна);

М_8-8 = М_5-5 = –17 кН∙м (растягиваются верхние волокна);

М_9-9 = –М–F₂∙1,5–q∙2∙1+F₁∙2 = ‑12–40∙1,5–10∙2∙1+30∙2= –32 кН∙м (растягиваются верхние волокна).

По полученным результатам строим эпюры M, Q, и N (рис. 2.17 а,б,в).

Проверки правильности построения эпюр методом вырезания узлов представлены на рис.2.16,б и 2.17,г.

ПРИМЕР 2

Построить эпюры M, Q и N для стержня с ломаной в плоскости осью (рис. 2. 18).

РЕШЕНИЕ

1. Вычислим необходимые для решения задачи геометрические характеристики:

sinα = 3/5 = 0,6; cosα = 4/5 = 0,8; tgα = 3/4 = 0,75.

2. Определяем опорные реакции.

∑Х = 0; q₁∙3 – H_B – F₂ = 0;

H_B = q₁∙3 – F₂ = 8∙3 – 16 = 8 кН.

∑М_В=0; –V_A∙8 – q₁∙3∙1,5 – M₁ + M₂ + F₂∙3 F₃∙2+q₂∙2∙1+F₁∙6=0;

V_A∙8 – 8∙3∙1,5 – 40 +80 + 16∙3 + 24∙2+20∙2∙1+20∙6=0;

∑М_А=0; V_B∙8 – q₁∙3∙1,5 – M₁ + M₂ + F₂∙3 -F₃∙6-q₂∙2∙7-F₁∙2=0;

V_B∙8 – 8∙3∙1,5 – 40 +80 + 16∙3 - 24∙6-20∙2∙7-20∙2=0;

Проверка: ∑Y=0; V_A+V_B –F₃ –q₂∙2–F₁=32,5+51,5-24-20∙2-20=0.

3. Пронумеруем грузовые участки – 1-6 (рис.2.18).

4. В пределах каждого грузового участка проводим сечения и положения этих сечений фиксируем координатой “x_i” от начала данного грузового участка

80

Рис.2.18

5. Используя сформулированные ранее рабочие правила и принятые правила знаков, записываем выражения для внутренних усилий – М, Q и N.

1-й грузовой участок: 0 ≤x₁≤2 (рассматриваем правую отсеченную часть).

N₁=0; Q₁=F₁=20 кН;

M₁(x₁)= –F∙x₁= –20∙x₁ (функция линейная, эпюру М на данном участке строим по двум сечениям):

x₁=0, М₁(0)=0;

x₁=2м, М₁(2)=–40 кН∙м (растягиваются верхние волокна).

2-й грузовой участок: 0≤x₂≤3м (рассматриваем нижнюю отсеченную часть).

N₂= –V_A+F₁= –32,5+20= –12,5 кН;

Q₂(x₂)= –q₁∙x₂= –8∙x₂ (функция Q линейная, ее график будем строить по двум точкам).

x₂=0, Q₂(0)=0,

x₂=3м, Q₂(3)= –8∙3= –24кН.

М₂(x) = F₁∙2 – q₁∙x₂∙x₂/2 = 20∙2 – 8∙x₂²/2 (квадратичная функция).

x₂=0, М₂(0)=40 кН∙м (растянуты правые волокна);

x₂=1,5м, М₂(1,5)=31 кН∙м (растянуты. правые волокна);

x₂=3м, М₂(3)= 4 кН∙м (растянуты правые волокна).

3-й грузовой участок:0 ≤x₃≤2 м (рассматриваем левую отсеченную часть).

N₃ = –q₁∙3 = –8∙3 =–24 кН; Q₃ = V_A–F₁ = 32,5 –20 = 12,5 кН.

М₃(х₃) = F₁∙(2-x₃) + V_A∙x₃ – q₁∙3∙1,5 + M₁ =

= 20∙(2-x₃) + 32,5∙x₃ – 8∙3∙1,5 + 40 =

= 20∙(2-x₃) + 32,5∙x₃ + 4; (функция линейная).

x₃ = 0, М₃(0) = 44 кН∙м, (растягиваются нижние волокна);

x₃ = 2, М₃(2) = 69 кН∙м, (растягиваются нижние волокна).

4-й грузовой участок: 0 ≤x₄≤2 м. (Далее рассматриваем правую отсеченную часть).

N₄ = –F₂ – H_B = -16-8 = –24 кН;

Q₄ = –V_B + F₃ + q₂∙2 = –51,5 + 24 + 20∙2 = 12,5 кН;

М₄(х₄) = V_B∙(4+x₄) – F₃∙(2+x₄) – q₂∙2∙(3+x₄) – H_B∙3 =

= 51,5∙(4+x₄) – 24∙(2+x₄) – 20∙2∙(3+x₄) – 8∙3; (ф–я линейна).

x₄=0, М₄(0)=51,5∙(4+0) – 24∙(2+0) – 20∙2∙(3+0) – 24 = 14 кН∙м;

(растягиваются нижние волокна).

x₄=2м, М₄(2)=51,5∙(4+2) –24∙(2+2) – 20∙2∙(3+2) – 24 = –11 кН∙м;

(растягиваются верхние волокна).

5-й грузовой участок: 0 ≤x₅≤2, y₅=x₅∙tgα.

N₅ = –V_B sinα – H_B cosα + F₃ sinα + q₂∙2∙sinα =

= –51,5∙0,6 – 8∙0,8 + 24∙0,6 + 20∙2∙0,6 = 1,1 кН.

Q₅ = –V_Bcosα – H_Bsinα + F₃cosα + q₂∙2∙cosα =

= –51,5∙0,8 – 8∙0,6 + 24∙0,8 + 20∙2∙0,8 = 14,8 кН.

M₅(х₅,у₅) = V_B∙(2+x₅) – H_B∙(1,5+y₅) – F₃∙x₅ – q₂∙2∙(1+x₅) =

= 51,5∙(2+x₅) – 8∙(1,5+y₅) – 24∙x₅ – 20∙2∙(1+x₅);(ф–я линейна):

x₅=0, y₅=0, М₅(0,0)=51,5∙2 – 8∙1,5 – 24∙0 – 20∙2∙1= 51 кН∙м.

x₅ = 2м, y₅ = 2∙0,75 = 1,5 м,

–

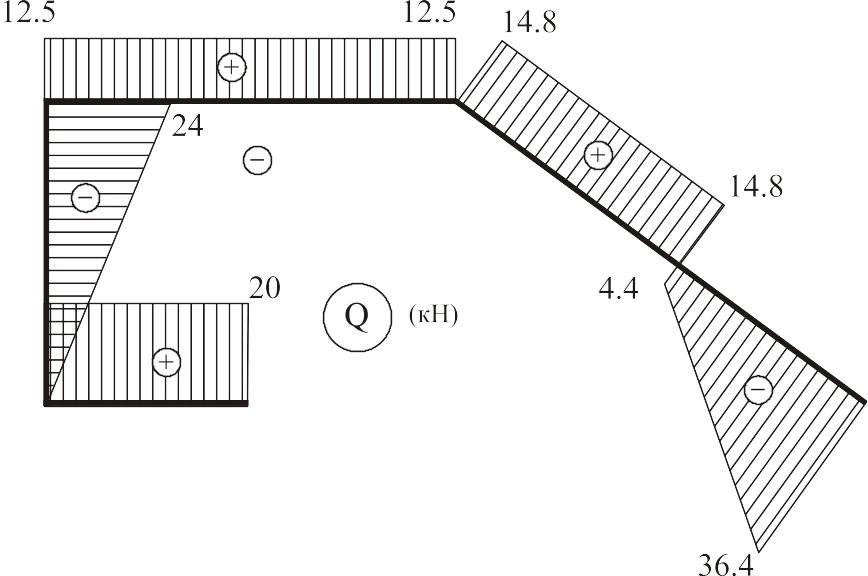
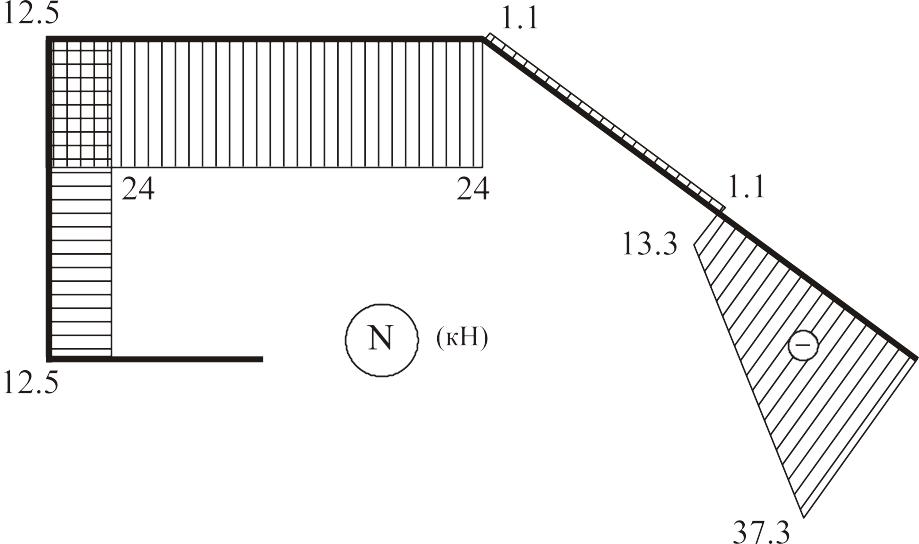
Рис.2.22

М₅(2;1,5) = 51,5∙(2+2) – 8∙(1,5+1,5) – 24∙2 – 20∙2∙(1+2)=

=14 кН∙м (растягиваются нижние волокна).

6-й грузовой участок: 0 ≤x₆≤2, y₆=x₆∙tgα.

N₆(х₆) = –V_Bsinα – H_Bcosα + q₂∙x₆∙sinα =

=–51,5∙0,6 – 8∙0,8 + 20∙x₆∙0,6 = –37,3 + 12x₆; (ф–я линейна):

x₆=0, N₆(0)= –37,3 кН; x₆=2м, N₆(2)= –13,3 кН.

Q₆(х₆) = –V_Bcosα + H_Bsinα + q₂∙x₆∙cosα =

= –51,5∙0,8 + 8∙0,6 + 20∙x₆∙0,8 = -36,4 + 16x₆; (ф–я линейна):

x₆=0, Q₆(0)= –36,4 кН; x₆=2м, Q₆(2)= –4,4 кН.

M₆(х₆,у₆) = V_B∙x₆ – H_B∙y₆ – q∙x₆²/2= 51,5∙x₆ – 8∙y₆ –20∙x₆²/2;

(функция нелинейная, график будем строить по трем точкам):

x₆=0, y₆=0, М₆(0,0)=0;

x₆=1 м, y₆=0,75м, М₆(1; 0,75)=35,5 кН∙м;

x₆ = 2 м, y₆ = 2∙0,75 = 1,5 м, М₆(2; 1,5)=51 кН∙м

(растягиваются нижние волокна).

По полученным данным строим эпюры М, Q и N (см. рис. 2.22).