1.4.2.Супутниковий метод

Для простоти приймемо Землю за кулю з центром у точці 0, а орбіту супутника К вважа­тимемо коловою. Нехай спостерігач знаходиться на полюсі в точці Р і вимі­рює кут і час t.

Позначимо радіус Землі і орбіти че­рез R і R₁. Початок системи координат візьмемо в центрі Землі. Координати супутника в момент t визначають за формулами:

X_k=R₁sin(ω₁t+a₀);

Y_k=R₁cos(ω₁t+a₀),

де ω₁ - кутова швидкість руху супутника; a₀ - кутове положення супутника на орбіті, яке відлічують від екватора в початковий момент.

З рис. 1.З видно, що

tgα= . (1.16)

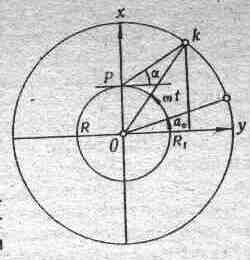
Рис. 1.3. До супутникового ме­тоду

Далі, застосовуючи третій закон Кеплера, згідно з яким квадрати періодів Т обертання небесних тіл відносяться як куби їхніх середніх відстаней R від притягаючого центра, напишемо:

(1.17)

де Т₁= - період обертання супутника; k = - постійний коефі­цієнт (для Землі він становить 4π²/398600 с²/км³); Т - період обер­тання Землі.

За формулами (1.16) і (1.17) можна скласти рівняння

α=arctg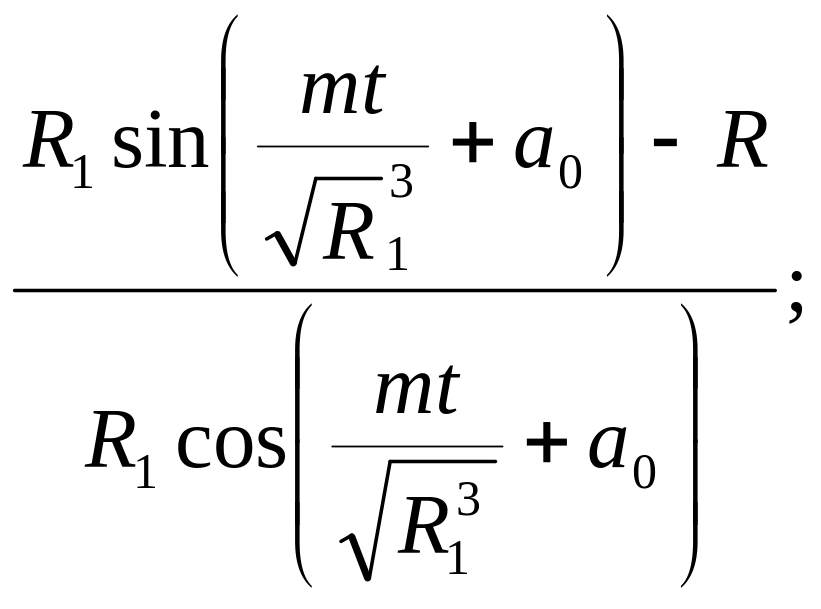 (1.18)

.

відносно невідомих R_, R₁ і а₀. Маючи багато результатів спостере­жень α і t, легко скласти систему рівнянь типу (1.18) і знайти радіус Землі та інші параметри.

У реальних умовах визначити розміри і форму Землі супутниковим методом набагато складніше. При цьому враховують еліпсоїдальність Землі. Орбіта супутника не може бути точним колом. Її визна­чають з високою точністю за спостереженнями супутника. На сьогод­ні точність передачі координат на великі відстані супутниковим мето­дом становить кілька метрів.

Найточніше гравітаційне поле Землі та її фігуру визначають за гра­віметричними й супутниковими даними. За даними супутника фігуру геоїда визначено з похибкою 4 м, велику піввісь земного еліпсоїда -з похибкою 5 м, а стиснення - з 0,002 знаменника.

2. Геометрія земного еліпсоїда

2.1. Параметри земного еліпсоїда, зв’язки між ними

Поверхня еліпсоїда утворюється від обертання еліпса навколо його малої (полярної) осі.

Будь-який еліпс визначається розмірами його великої а і малої b півосей (рис. 2.1). За розмірами півосей можна знайти положення фокусів F₁ і F₂ еліпса

OF₁=OF₂=

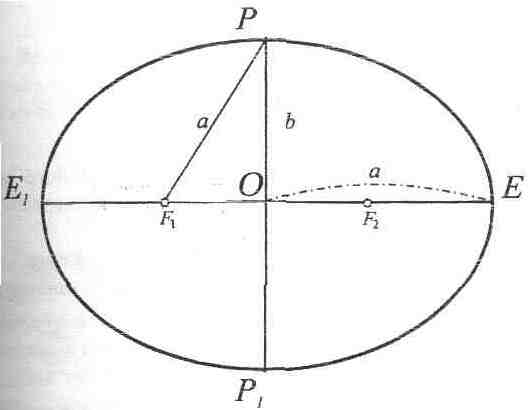
Рис. 2.1

Відносна величина, що визначається зі співвідношення, називається першим ексцентриситетом еліпса.

, (2.1)

Мають застосування й інші відносні величини: другий ексцентриситет

, (2.2)

полярне стиснення

. (2.3)

Розміри еліпса визначаються розмірами його великої півосі а. Форма еліпса визначається однією із наведених вище відносних величин, найчастіше це стиснення α

Крім великої та малої півосей еліпса, часто засто-совується ще одна лінійна величина, що визначається зі співвідношення

(2.4)

Наведені лінійні та відносні величини еліпса називаються параметрами еліпса і відносяться й до еліпсоїда обертання. Параметри а - велика (екваторіальна) піввісь еліпсоїда і b - мала (полярна) піввісь еліпсоїда або а і α називають основними параметрами, що визначають еліпсоїд обертання, а квадрати першого та другого ексцентриситетів – е² та е'² – похідними.

Між перерахованими величинами існують залежності. Так, із (2.1) та (2.2) отримаємо:

,

( 2.5)

Враховуючи вище наведені залежності для полярного стиснення α та першого ексцентриситета е, отримаємо такі формули зв'язку

( 2.6)

Для виводу числових значень параметрів земного еліпсоїда, переважно великої півосі та стиснення, використовуються відповідні геодезичні, астрономічні, гравіметричні та супутникові виміри.

Для наближених розрахунків можна використовувати наступні значення:

a=6378 км,

a-b=21км,

Відомо багато еліпсоїдів, параметри яких визначались у різних регіонах Землі і названі на честь видатних вчених, керівників робіт, що їх визначали або стали Міжнародними (див.табл.2.1):

Таблиця 2.1

Назва Еліпсоїда	Екваторіальний радіус, м	Стиснення
1	2	3
Красовського (1940)	6378245	1/298,3
Міжнародний (1924)	6378388	1/297
Кларка (1880)	6378249,145	1/293,465
1	2	3
Бесселя (1841)	6377397,155	1/299/1528128
Ері (1830)	6377563,396	1/299,3249646
Евереста (1956)	6377301,243	1/300,8017
Гельмерта (1906)	6378200	1/298,3
Південноамериканський (1969)	6378160	1/298,25
WGS72 (1972)	6378135	1/298,26
GRS80 (1979)	6378137	1/298,257222101
WGS84	6378137	1/298,257223563

Для еліпсоїда Красовського, що застосовується у гео- дезичних роботах в Україні, крім основних параметрів (див. табл. 2.1), згідно з наведеними вище формулами зв'язку, маємо:

b= 6356863.01877;

e²=0.006693421623;

е '² = 0.00673 8525415.

На даний час, згідно з резолюцією XVII Генеральної Асамблеї Міжнародної геодезичної та геофізичної спілки (Канберра, 1979), офіційною референцною системою Міжнародної асоціації геодезії є Геодезична Референцна Система 1980 року - GRS-80. Ця система визначає основні параметри загального земного (глобального) еліпсоїда. Серед них

а =6378137м,

Починаючи з 1987 року, глобальна система визначення місцеположення (GPS) використовує, як опорну, Світову геодезичну систему WGS-84. Поверхнею віднесення цієї системи є геоцентричний еліпсоїд обертання з параметрами:

Зазначимо, що прийняття загального земного чи ре-ференц-еліпсоїда, тобто його розмірів, є одним з основних чинників, що характеризує певну систему геодезичних координат.