11.6. Врівноваження нівелірних мереж

Обробку високоточного нівелювання виконують так. Спочатку визначають перевищення за окремими ходами між фундаментальними реперами. Потім вводять поправки за непаралельність рівневих по­верхонь. Після цього, залежно від конфігурацій нівелірної мережі, врів­новажують її за корелатним або параметричним методом.

На рис. 11.10 і 11.11 зображено дві нівелірні мережі. Перша з них вільна, а друга - невільна, вона має два пункти, висоти яких треба визна­чити. Стрілками показано напрямки ходів; h₁, h₂, h₃,…- виміряні пе­ревищення. Висоти точок А, С, D і F відомі; Н_A, H_B і т. д. Як легко встановити, першу мережу простіше врівноважити корелатним мето­дом, другу – пара-метричним. Для цього потрібно підрахувати число необхідних і надмірних вимірювань.

Корелатний метод. Умовне рівняння складається для кожного замкнутого ходу (або полігону), в якому є один надмірний вимір. На­приклад, додаючи врівноваженні пере-вищення до висоти точки А у мережі на рис. 11.10 і йдучи по замкнутому ходу, ми повинні прийти до точ­ки А й одержати її висоту:

H_A + h₁ + v₁ ⁺ h₆ + v₆ + h₉ + v₉ + h₇ +v₇ = H_A;

v₁ + v₆ + v₇ +v₉ +W₁ = 0; (11.1)

W₁ = h₁ + h₆ + h₇ + h₉ ,

де v₁ , v₆ - поправки в перевищення.

Отже, в мережі на рис. 11.10 є чотири надмірних виміри. Використовуючи геометричну умову (сума вирівняних перевищень у полігоні по­винна дорівнювати нулю) в полігонах І, II, III й IV, неважко скласти чо­тири умовних рівняння виду (11.1).

Якщо довжини ходів нівелювання набагато відрізняються один від одного, то вводять вагу вимірювань і враховують її при складанні рівнянь. Визначають, що вага буде такою:

Вважаючи, що постійна С = η², знайдемо

(11.2)

де L - довжина ходу нівелювання.

Параметричний метод. Рівняння поправок для кожного виміряного перевищення складають на підставі таких міркувань (рис.11.11):

H_B – H_A = h₁ + v₁ ;

v₁ = H_B + l₁ ;

l₁ = - H_A – h₁ , (11.3)

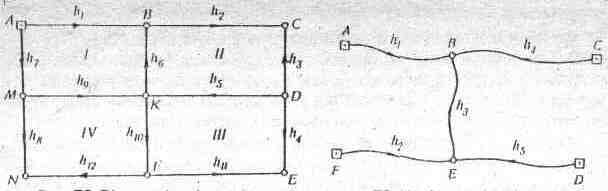
Рис. 11.10. Вільна нівелірна мережа Рис.11.11. Невільна нівелірна мережа

H_E – H_B = h₃ + v₃;

v₃ = H_E – H_B + l₃ ; (11.4)

l₃ = - h_{3 ,}

де Н_B, Н_E - невідомі висоти, які знаходять з розв'язання нормаль­них рівнянь; l₁, l₃ - вільні члени рівнянь поправок (11.3) і (11.4).

Точність врівноваженних перевищень або висот пунктів оцінюють за відомими правилами. Для оцінюваних перевищень або для висот складають вагові функції і дописують їх до умовних рівнянь і т. д. На­приклад, вагова функція для перевищення h₁₁ має такий вигляд:

dF₁₁ = v_{11 ,} (11.5)

а вагову функцію для висоти точки Е на рис. 11.10 можна записати так:

dF_E = v₇ + v₉ + v₁₀ + v₁₁ . (11.6)

11.7. Короткий історичний нарис

Перші нівеліри були гідростатичними, побудованими за фізичним законом про сполучені посудини. Ними користувалися в УІ-ІІ ст. до н. е. стародавні греки. Нівелір з астрономічною трубою було створено у другій половині XVII ст. Ним користувалися Пікар та Гюйгенс для ні­велювання земної поверхні. Горизонтально нівелір встановлювали за допомогою виска. У 1820 р. французький інженер Его сконструював глухий нівелір з рівнем на підставці. Через деякий час з'явилися ні­веліри з рівнем при трубі. Перший такий нівелір було сконструйовано в Німеччині. Більш досконалі нівеліри - з оптичним мікрометром - з'явилися в першій половині XX ст. в Австрії та Німеччині.

Роботи з високоякісного нівелювання було розпочато в Швейцарії та Саксонії в 1865 р., Пруссії - в 1867 р., Баварії - в 1868 р., Росії - в 1873 р., Австро-Угорщині й Італії - в 1874 р., Франції - в 1884 р.

Створення нівелірної мережі в Росії було розпочато Військово-топографічним відділом Генерального штабу в 1871 р. За 1871-1893 рр. На території європейської частини Росії було прокладено майже 13000 км нівелювань. Результати цієї роботи подано в каталозі С. Д. Рильке. Корпус військових топографів до 1917 р. виконав понад 45000 км ні­велювань. Вище геодезичне управління за перші 10 років свого існу­вання з 1919 по 1929 р. проклало понад 15000 км нівелірних ліній. У 1932 р. видано Каталог реперів і марок ГТУ та УВТ.

Не припиняються роботи з високоточного нівелювання і в наступні роки. Так, за 1950-1963 рр. прокладено майже 25000 км ліній ніве­лювання І класу. З 1949 по 1964 р. виконано близько 50000 км ліній нівелювання II класу. Ще в більшому обсязі виконується нівелювання тепер.

Загальне вирівнювання нівелірної мережі СРСР було розпочато в 1931р. й закінчено в 1954 р. У 1969 р. здійснено четверте вирівнюван­ня нівелювань І та II класів.