8.2. Базисний прилад бп-1

Дротяний базисний прилад БП-1 принципово не відріз-няється від аналогічних приладів, які вивчаються у початко-вому курсі геодезії, Тому обмежимося загальними відомостя-ми і детально розглянемо теорію обробки вимірювань.

Базисний прилад з дротинами винайшов у 1884 р. шведський уче­ний Е.Едерін, Це стало видатним досягненням у геодезії, тому що ви­мірювати довжини раніше було дуже важко й складно. Спочатку дро­тини виготовляли зі сталі й латуні. На початку XX ст. французький учений Ш. Гільом відкрив інвар, і дротини почали виготовляти з нього, а дротя-ний прилад назвали приладом Едеріна - Гільома. В Росії перші базисні вимірювання з дротинами виконано в 1888 р. за участю само­го Е. Едеріна.

До комплекту БП-І входять: 1) 8 інварних дротин 24 м завдовжки; 2) інварна стрічечка 12 м завдовжки для вимірювання залишку базису, який не дорівнює довжині дротини; 3) 2 блочні станки з гирями масою 10 кг для підвішування дротин; 4) 40-50 шт. штативів базисних із ціликами; 5) термометр-пращ для вимірювання температури по­вітря; 6) два оптичних центрири, які встановлюють над центрами ба­зисних пунктів, що фіксують кінці секції лінії; 7) нівелір підвищеної точності з двосторонньою рейкою 1,5-2 м завдовжки для нівелювання ціликів; 8) теодоліт для про­вішування вимірюваної лінії; 9) карабіни для дротин та інше приладдя.

На кінцях дротин, діаметр яких близько 2 мм, закріп­лено шкали 8 см завдовжки з поділками через 1 мм. По­ділки шкал збільшуються в один бік. Довжина дротини, рівна відстані між нульовими поділками шкал, становить 24 м.

На рис. 8.1 схематично показано дротину зі шкалами, гирі по 10 кг, цілики А і В, напрямок ходу вимірювань; l₀ – довжина шкали між нулями шкал; l – довжина хорди між ціликами. З рисунка випливає що

(8.1)

де П,З – відліки по передній і задній шкалах.

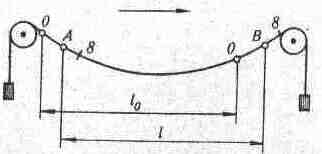
Рис. 8.1. До визначення довжини хорди

8.3. Поправки, які вводяться у довжину хорди. Виведення формул

У польові вимірювання з дротяним приладом БП-1 вводять такі поправки: 1) за компарування; 2) за температуру Δ_t; 3) за приведення до горизонту Δ_h; 4) за проектування на поверхню еліпсоїда Красовського Δ_H; 5) за зміну сили ваги Δ₁; 6) за нахил шкал Δ₂; 7) за несиметрію ланцюгової лінії Δ₃; 8) за неточність поділок шкал Δ₄. Розглянемо ці поправки детальніше.

Поправка за компарування. Дротини компарують двічі: перед початком польових вимірювань і в кінці. Поправку за компарування вводять за формулою

Δl_k=nΔl₀, (8.2)

де n- число проміжок у секції; Δl₀, - середнє арифметичне з попра­вок, знайдених при першому й другому компаруваннях.

Поправка за температуру повітря. Колір інвару нагадує колір повітря, тому вважають, що температура навко-лишнього повітря така сама, як і дротини. Температуру повітря спеціальним термометром (термометром-пращом) вимірюють до 0,1 °С. При цьому беруть до уваги середню температуру секції t. Температуру компарування t₀ приймають рівною 20 °С.

Щоб вивести формулу, за якою визначають поправку за темпера­туру, користуються розкладанням:

Вважаючи, що

і написавши два очевидних рівняння

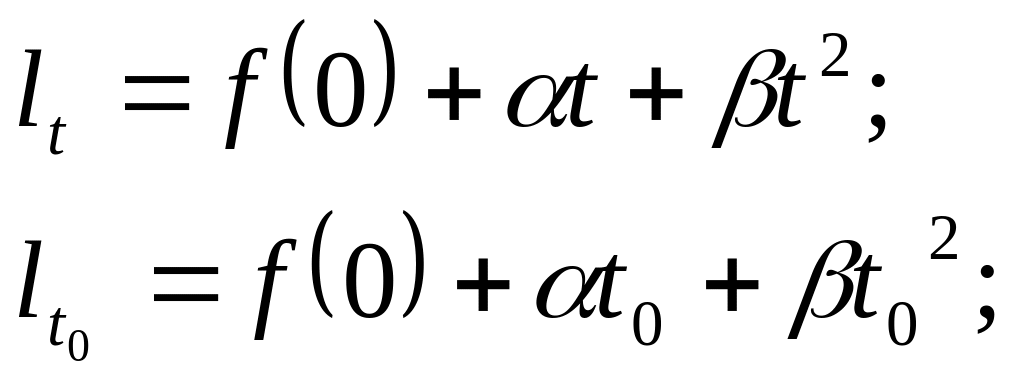
одержимо необхідну формулу, за якою визначають поправку за тем­пературу повітря,

( 8.3)

де , - температурні коефіцієнти дротини.

Поправка за нівелювання ціликів. Поправку за перевищення ціликів у проміжку (за нівелювання ціликів або за приведення хорди дротини до горизонту) визначають за формулою, яку виводять з таких очевидних рівнянь:

( 8.4)

де l - нахилена хорда дротини; l’ -її горизонтальна складова; h - перевищення між ціликами в проміжку.

Поправка за проектування на еліпсоїд. Цю поправку вводять у довжину всієї вимірюваної лінії, приведеної до горизонту. Нехай Н - се­редня висота вимірюваної лінії D₀ над геоїдом; - середня висота геоїда над еліпсоїдом у даній місцевості; R - середній радіус кривиз­ни нормального перетину еліпсоїда вздовж вимірюваної лінії; D -проекція D₀ на поверхню еліпсоїда Красовського. Тоді з елементар­них міркувань одержуємо:

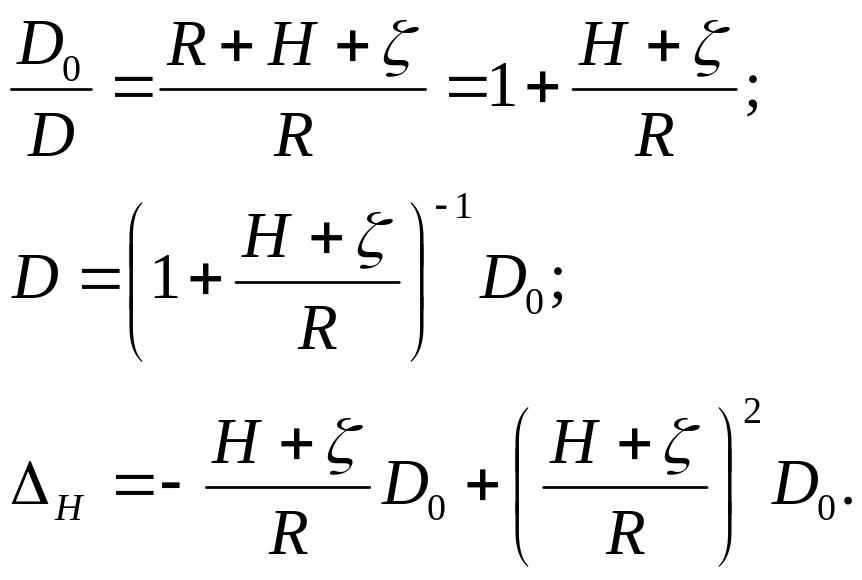
(8.5)

Поправка за зміну сили ваги. Сила ваги на земній поверхні змінюється мало. Так, земне прискорення на полюсі й екваторі відріз­няється всього на 0,05 м/с². Однак зміну сили ваги доводиться вра­ховувати при вимірюванні довжин дротинами.

Зміну сили ваги можна виміряти за допомогою маятникових при­ладів і гравіметрів. Значення земного прискорення наближено обчис­люють за формулою q=978051(1 + 0,0053035 sin²φ - 0,0000059 sin² 2 φ) - 0,3086Н + +Δ q, (8.6)

де q - земне прискорення, мгл; φ - астрономічна широта пункту; H -висота пункту над рівнем моря, м; Δ q - аномалія сили ваги, знята з гравіметричної карти, мгл.

За формулою (8.6) можна обчислити земне прискорення для Москви, де компарували дротини, і для місця вимірювання лінії. Нехай маса гирі P у Москві становить mq, а в районі польових робіт з дро­тинами – mq₂, де т- маса нерухомої гирі. Зміна маси гирі, очевидно, така: m(q₂-q₁)₌mδq. Диференціюючи формулу (8.7), одержимо:

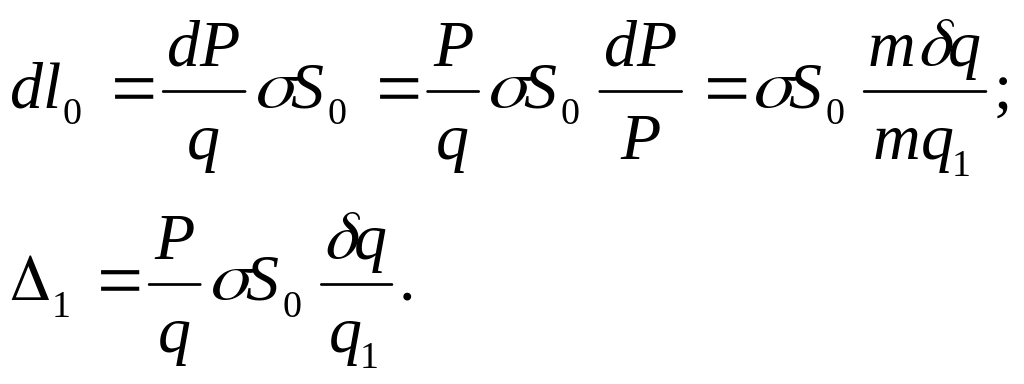
(8.8)

У формулі (8.7) перший і третій доданки праворуч не залежать від q (тому що в числівнику q і в знаменнику Р залежать від q; однак дріб q/Р не залежить від q). У другому доданку дріб σ/q не залежить від q, але Р залежить від q.

Поправка за нахил шкал. У випадку, коли хорда дротини горизонтальна, шкали нахилені до горизонту на однаковий кут α, який визначають за формулою

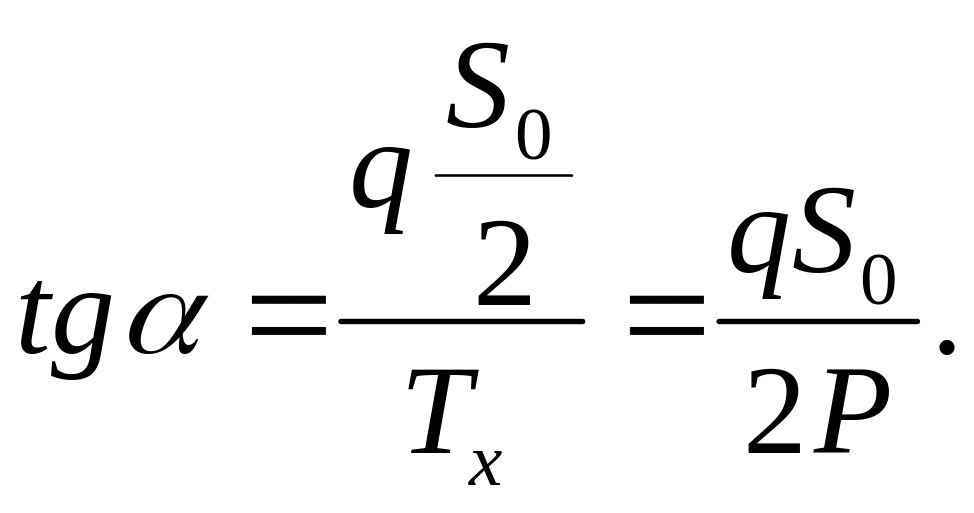
(8.9)

У свою чергу

Виходить, формула поправки за нахил шкал буде такою:

(8.10)

Рис.8.2. До несиметрії дротини

Поправка за несиметрію ланцюгової лінії. При наявності перевищення між ціликами А і В дротина розміщується несиметрично щодо хорди (рис. 8.2). При цьому виявляється, що хорда l довша за хорду l₀ . Різницю між ними можна знайти з розв'язання фізичної задачі. Не спиняючись на досить складному виведенні, наводимо остаточну формулу

(8.11)

Поправка за неточність поділок шкал. Під час компарування дротин за допомогою мікроскоп-мікрометрів за певною програмою дослід­жують точність кожної поділки шкал дротин. Якщо похибки поділок значні, то складають спеціальну таблицю від 1 до 80 поділок з ураху­ванням поправок за неточність; за таблицею можна враховувати не­точність поділок шкал.