Розв'язуючи ці рівняння за методом найменших квадратів, утво­римо функцію

Взявши окремі похідні по x і y та прирівнявши їх до нуля, одержимо нормальні рівняння:

Отже, вирівняні значення необхідних кутів визначимо за форму­лами:

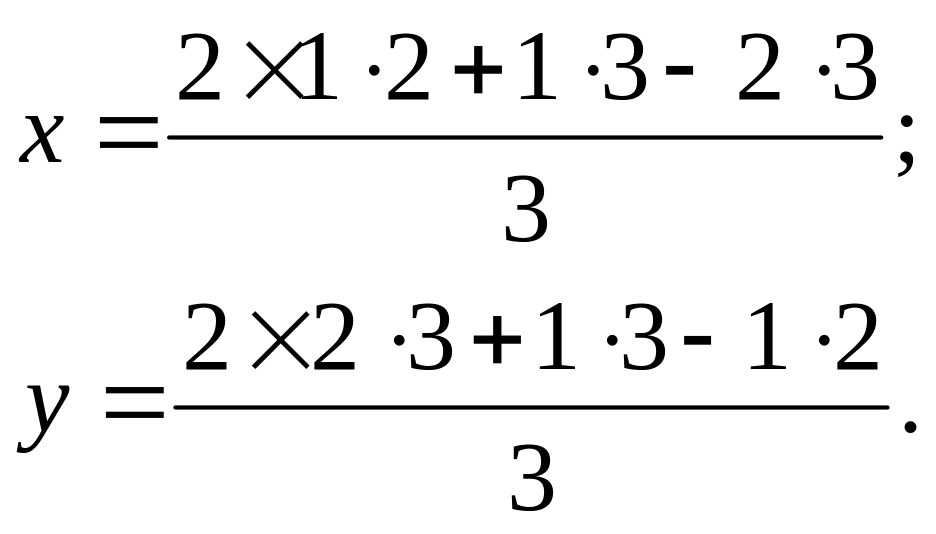
(7.10)

Аналогічні формули можна одержати для будь-якого числа на­прямків п. Вони дають змогу зробити такий висновок: якщо приписати до безпосередньо виміряного кута ( або ) вагу 2, а до обчи­слених таких самих кутів (за іншими виміряними кутами) вагу 1, то вирівняний кут знаходять як середнє вагове значення.

Для запам'ятовування і зручності обчислень введемо фіктивні (що дорівнюють нулю) кути потім вважатимемо, що .Тоді спільна формула, що визначає вирівняний кут, буде такою:

(7.11)

При п = 3 маємо:

Для зручності обчислень складемо таблицю при п = 4 (табл. 7.1).

Таблиця 7.1.

Значення кутів при т прийомах

1 ·1	2 ·1	3·1	4·1
1 ·2	2·2	3·2	4 ·2
1·3	2 ·3	3·3	4 ·3
1·4	2·4	3·4	4 ·4

Записавши в табл. 7.1 значення кутів, одержаних з т прийомів, і користуючись спільною формулою, легко обчислити вирівняне зна­чення будь-якого кута. Таких способів обчислення може бути кілька.(Подумайте про це!).

Таким чином, усі кути. які потрібно визначити, слід вимірювати по можливості в різних умовах. Не реко-мендується один і той самий кут вимірювати кількома прийо-мами підряд. Програму спостережень по­трібно виконувати так, щоб протягом одного дня було виміряно якнайбільше число різних кутів.

Метод вимірювання напрямків круговими прийомами. Цей метод застосовують для вимірювання напрямків, а не кутів. Його запропо­нував відомий російський астроном і гео-дезист В.Я.Струве при ви­конанні Балтійської частини велико-го російського градусного вимі­рювання (1816-1852 рр.).

Вимірювання напрямків способом кругових прийомів полягає в то­му, що труба теодоліта послідовно наводиться на всі напрямки станції, починаючи з першого і закінчуючи також першим. У першому напівприйомі алідаду обертають за ходом годинникової стрілки, у друго­му - проти. У пер-шому напівприйомі трубу трохи переводять через предмет (як видно в трубу), а в другому - трохи не доводять до нього. При цьому вертикальні нитки завжди після закінчення грубого переміщення виявляться ліворуч від предмета, так що остаточне наве­дення завжди виконуватиметься тільки угвин-чуванням навідного гвинта алідади. При спостереженнях трубу між. першим, і другим напівприйомами переводять через зеніт. Якщо користуватися інстру­ментами з мікроскоп-мікрометрами, то трубу перекладати в лагерах між напівприйомами не обов'язково. Однак на кожному пункті поло­вина програми виконується при одному положенні верти-кального круга, а друга половина - при другому. При візуванні по кожному на­прямку відліки беруть по кругу. Передбачено замикання горизонту на початковому напрямку. Тому різниця у відліках при візуванні по цьо­му напрямку (одержаних на початку і в кінці прийому), зумовлена тільки помилками спостережень у напівприйомі, усувається або ви­веденням середнього з двох відліків, або розподілом нев'язки по всіх напрямках. Щоб результати вимірювань по всіх напрямках у прийомі привести до початкового (нульового) напрямку, відлік по першому напрямку віднімають з усіх останніх.

При способі кругових прийомів горизонтальний круг між прийома­ми переставляють на величину

де т - число прийомів; і - найменша поділка горизонтального круга.

Складають також робочу таблицю установок лімба.

Обробка вимірювань, як це можна показати за допомогою методу найменших квадратів, полягає у виведенні середніх значень по кож­ному напрямку зі значень усіх виконаних прийомів.

Середню квадратичну похибку напрямку, одержаного з одного прийому, обчислюють за точною формулою

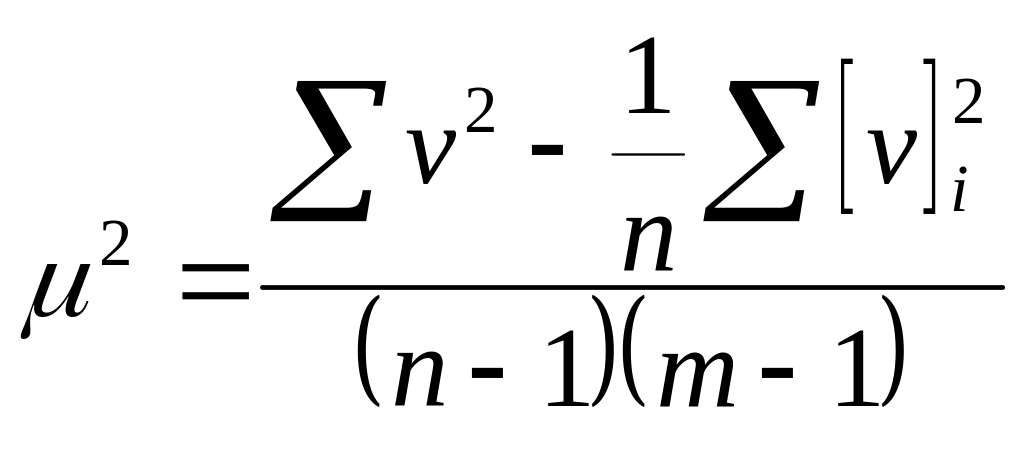
(7.12)

або наближеною

(7.13) де - відхилення значень виміряних у прийомах напрямків від серед­нього арифметичного; - сума абсолютних вели-чин відхилень виміряних напрямків від їх середніх значень; п - число напрямків; т- число прийомів.

Похибку вирівняного на станції напрямку обчислюють за формулою

(7.14)

У 1831-1834 рр. Ф.Бессель виконував градусні вимі-рювання у Східній Пруссії, де використав метод вимірювання напрямків (без замикання горизонту), який застосовували на той час англійці.

Метод „неповних прийомів" для вимірювання напрямків запропо­нував у 1954 р. інженер Ю. А. Аладжалов. Суть його полягає в тому, що замість вимірювання одиночних кутів у всіх комбінаціях вимірю­ють напрямки (без замикання горизонту) окремими групами за трьо­ма напрямками. При цьому групи напрямків підібрано так, що за ре­зультатами вимірювань можна обчислити всі кути, які треба виміряти способом усіх комбінацій. Ці вимоги повністю реалізуються на стан­ціях, де виконуються такі умови: число напрямків має бути непарним і величина п(п- 1)/2 повинна ділитися на три. До таких належать станції з п = 3, 7, 9, 13, 15 ... В усіх інших випадках на станції, крім ок­ремих груп по три напрямки, залишиться деяка кількість поодиноких кутів, які належить вимірювати, як і в способі в усіх комбінаціях.

Наприклад, при числі напрямків на станції п = 7 окремі групи по три напрямки і кути в усіх комбінаціях із семи елементів по два такі:

При п = 8, коли не виходять повністю окремі групи по три напрям­ки, маємо:

тобто вийшло сім груп по три напрямки і сім окремих кутів.

Залежно від числа напрямків і прийнятої на станції ваги гру­пи, які складаються з трьох напрямків, спостерігають 3/2 т прийома­ми, а поодинокі кути, якщо вони є, - т при-йомами, де т - число при­йомів вимірювання кутів у способі в усіх комбінаціях з тим самим числом і вагою.

Групи, які складаються з трьох напрямків, спосте-рігаються так само, як і в способі кругових прийомів, але без замикання горизонту.

Кут перестановки лімба між прийомами обчислюють за формулою

де т - число прийомів.

Кут перестановки лімба між групами визначають так:

де S - число груп і окремих кутів, які не увійшли в групи.

Вирівнювання на станції складається з таких етапів:

1) у кожній групі по три напрямки знаходять середнє арифметичне з числа прийомів для кожного напрямку; якщо є окремі кути, то для них також виводять середнє значення з m прийомів;

2) за середніми арифметичними напрямками обчислюють кути у найрізноманітніших комбінаціях;

3) за формулами обробки кутів у всіх комбінаціях визна-чають ви­рівняне значення кожного кута.

Середні квадратичні помилки кутів і напрямків обчислюють за та­кими формулами:

а) виміряного кута (середнього з т прийомів - для поодинокого кута і 3/2 т- для кутів, утворених трьома напрямками)

(7.15)

б) вирівняного на станції напрямку

(7.16)

в) вирівняного на станції кута

де v - відхилення виміряного кута від його вирівняного значення; п - число напрямків на пункті; r - число поодиноких кутів, виміряних ок­ремо від груп трьох напрямків.

Видозмінений спосіб вимірювання кутів у комбінаціях запропонував у 1950 р. інженер А. Ф. Томілін. Згідно з цим способом, на станції з n напрямками вимірюють такі кути:

тобто вимірюють усі кути між суміжними напрямками і всі кути, які є сумою двох суміжних кутів. Число всіх виміряних кутів дорівнює 2 n, де n - число напрямків на станції.

Вимірювання окремих кутів теодолітами з мікроскоп-мікрометра­ми у мережах 2 класу виконують п'ятьма, а оптич-ними теодолітами - шістьма прийомами. Кожний кут вимі-рюють за такою самою методи­кою, як і в способі вимірюван-ня кутів в усіх комбінаціях.

Перестановку лімба при вимірюванні кутів розраховують, виходячи з таких міркувань. Число виміряних кутів на станції 2п, з яких тих, що не прилягають один до одного: при п парному - п/2, при п непарному - (п-1)/2. Тому при п парному установки треба зміню­вати чотири рази (2п: п/2); при п непарному - п'ять разів {2п: (п-1)/2}- незалежно від того, що при діленні виходить дріб.

Обробку вимірювань розглянемо, коли число напрямків буде п = 3. У цьому випадку вимірюють такі кути:

Застосуємо параметричний метод вирівнювання. Рівняння попра­вок для кожного виміряного кута мають такий вигляд:

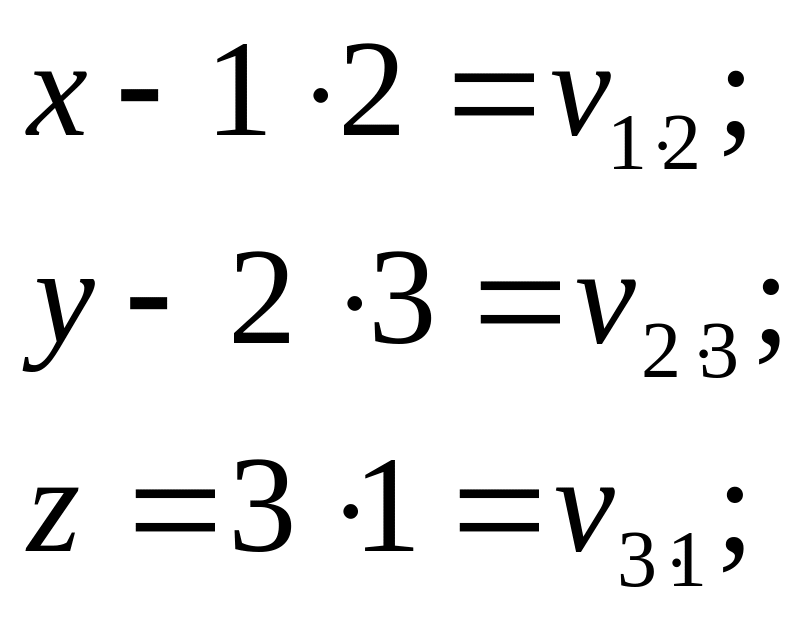
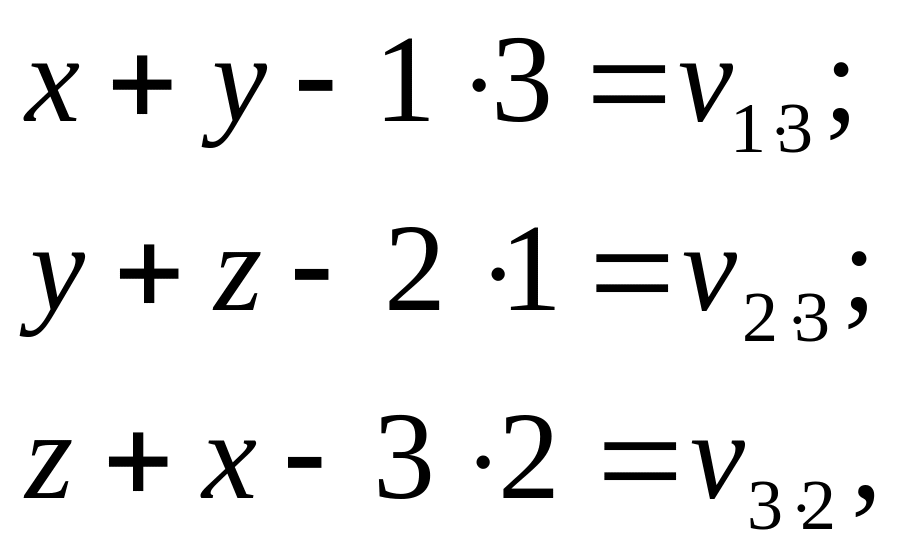
де x, y, z - значення вирівняних кутів i ; v - поправки у виміряні кути.

Щоб не мати справи зі значними величинами, припустимо, що х= і шукатиме-мо не х, y, z, а поправки в кути Рівняння поправок при цьому зміняться:

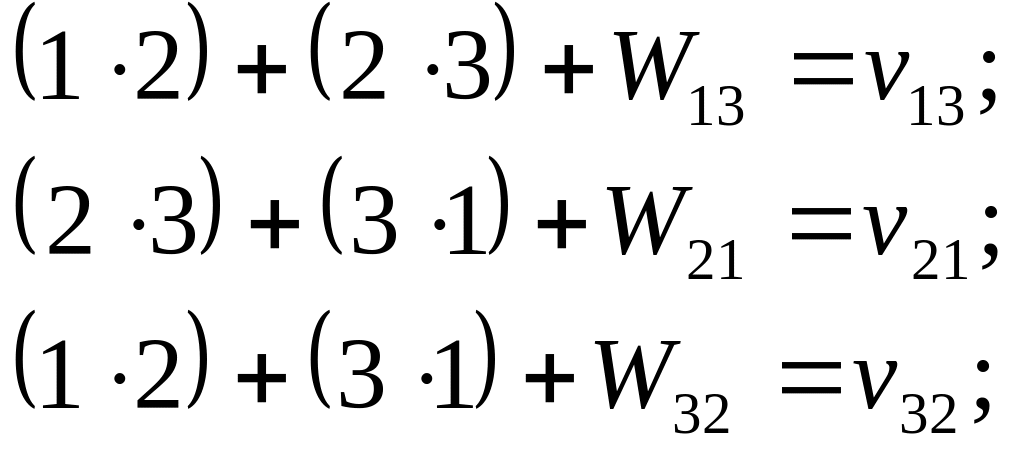
Поправки залежні між собою, тому при скла­данні функції Лагранжа необхідно цю залежність враховувати. Напи­шемо функцію Лагранжа

Ф=

де k- корелата умовного рівняння горизонту; W - вільний член.

Беручи окремі похідні за поправками і прирів­нюючи їх до нуля, після перетворень одержуємо нормальні рівняння:

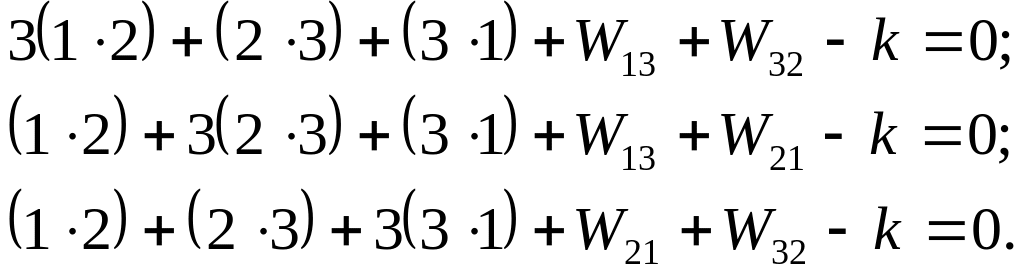
Склавши ці рівняння, знайдемо:

Врахувавши рівняння горизонту, одержимо корелату

Підставляючи значення корелати в нормальні рівняння і розв'я­зуючи їх, знаходимо невідомі поправки:

( 7.17)

Аналогічно можна одержати формули, за якими визначають по­правки у виміряні кути для п = 7,8,9.

Середню квадратичну похибку одиниці ваги, тобто кута, виміряно­го т прийомами, обчислюють за формулою

(7.18)

де v - різниця виміряного і вирівняного кутів.

Помилка кута, виміряного одним прийомом, дорівнювати-ме вели­чині , помноженій на корінь квадратний з числа прийомів, яким ви­міряно кожний кут. Середню квадратичну похибку вирівняного на станції кута визначають за формулою

де P₇=2,39; P₈=2,37; P₉=2,35.

Такі методи високоточних кутових вимірювань, що засто-совують­ся у тріангуляційних мережах.