6.4.Зорові труби. Окулярні мікрометри

Зорові труби, які застосовують у геодезичних приладах, винай­шли в 1609 р. голландець Г. Ліппергей, у 1609 р. – відо-мий італійський вчений Г. Галілей і в 1611 р. - німецький астроном Й, Кеплер. Пізніше в Англії винайшли сітку ниток (В. Гаскойн) і окуляр (Д. Рамсден).

Тоді зорові труби називались астрономічними, або трубами Кеплера. З часом їх удосконалювали й ускладню-вали.

Труба Кеплера має довгофокусний об'єктив, який дає справжнє зображення предмета в його фокальній площині, й короткофокусний окуляр, що виконує роль лупи. Трубу на предмет наводять за допомогою сітки ниток, розміщеної у фокусі об’єктива. Сітка ниток, вигравірована на скляній пластинці, складається з горизонтальної нитки і вертикальної (останнім часом - вертикального бісектора ниток).

Якість зорової труби залежить від кута поля зору, збільшення, яке визначається відношенням діаметра об'єктива до діаметра окуляра, і роздільної здатності, що дає змогу бачити в трубу два предмети, роз­міщені на дуже близькій відстані:

(6.6)

де Г, - збільшення і роздільна здатність труби; , - фокусна відстань об'єктива й окуляра труби.

Зорову трубу регулюють так. Спочатку окуляр встановлюють на фокус по нитках сітки (щоб було чітке зображення сітки ниток). Потім, переміщуючи сітку ниток разом з окулярним коліном, домагаються, щоб площина сітки збіглася з фокальною площиною об'єктива, у якій знаходиться зображення предмета. В оптичних теодолітах наведення на фокус регулюють переміщенням уздовж осі зорової труби спеці­альної розсіюючої лінзи, розміщеної між об'єктивом і фокусом (внут­рішнє фокусування). Це пристосування гаран-тує найліпшу стійкість регулювання труби.

З тілом зорової труби скріплені цапфи, якими зорова труба спира­ється на дві колонки, встановлені на алідаді. При ви-готовленні вісь цапф ставлять перпендикулярно до гео-метричної осі зорової труби. Цапфи за формою циліндричні, добре виточені і повинні бути продов­женням одна одної. Цих умов при виготовленні дотримуватися дуже складно.

Окулярні мікрометри. Труби сучасних високоточних теодолітів мають окулярні мікрометри (рис. 6.8). Окулярний мікрометр склада­ється з коробки 1, закріпленої нерухомо на окулярній частині; мікро­метричного гвинта 2 з барабаном поділок 3; рамки або рухомої карет­ки 4 з сіткою ниток 6 (бісектор вертикальних ниток); нерухомої плас­тинки 7, у ниж-ній частині якої є зубці (гребінка); двох спіральних пру­жин 5 для плавного поступального переміщення каретки 4. Барабан 3 розділений на 100 поділок. Ціна однієї поділки становить близько 1". Фокусною відстанню об'єктива і кроком мікрометричного гвинта ви­значають кутову величину оберту барабана:

( 6.7)

де R - ціна оберту барабана мікрометра; d - крок мікрометричного гвинта; f_об,- фокусна відстань об'єктива труби.

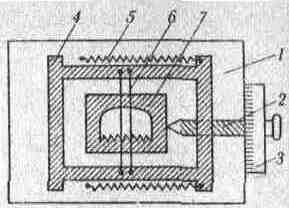
Рис.6.8. Cхема окулярного мікрометра

На коробці мікрометра перед барабаном є індекс для взяття від­ліків за барабаном. За один оберт барабана рухома нитка сітки ниток переміщується на одну поділку гребінки. Зубці гребінки, виходить, служать лічильниками числа обертів барабана. Початок відліку по гребінці береться від найбільшого вирізу, який називається нуль-пунктом гребінки (рис. 6.9).

Зорова труба в теодоліті пере­кладається в лагерах або пере­водиться через зеніт. Барабан окулярного мікрометра при цьому може бути праворуч або ліворуч від труби. Якщо барабан знаходиться праворуч від труби, то при обертанні мікрометричного гвин­та за годинниковою стрілкою (угвинчування) бісектор вертикаль­них ниток переміщується до бара­бана, пружини 5 розтягуються і відліки, по гребінці зростають (7, і 8, 9... обертів барабана). У нуль-пункті гре-бінки рахується 10 обертів, а на барабані при цьому - нуль поділок (за індексом). Прий­нято бісектор наводити на предмет угвинчуванням барабана (а не ви­гвинчуванням), тому що пружини 5 на стиснення і розтягування реа­гують по-різному. При розтягуванні пружини рама 4 переміщується більш плавно й рівномірно, ніж при стисненні.

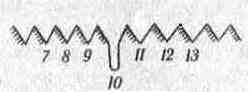
Рис.6.9. Схематичний рисунок гребінки

Розглянемо, як визначаються поправки до відліків по горизонтально­му кругу теодоліта за показами окулярного мікрометра головної труби і перевірочної. На рис. 6.10 ОА - візирна вісь зорової труби тео­доліта; ОМ - напрямок на предмет; ОР - прямовисна лінія; ON₁N₂ - частина горизонтального круга; PN₁,PN₂ am і N₁N₂ - дуги великих кругів сфери довільного радіуса, проведеній з точки O; - відлік по барабану окулярного мікрометра; х - поправка у відліки по горизон­тальному кругу; z - зенітна відстань предмета. Згідно з правилом Непера, з прямокутного сферичного трикутника aPm маємо:

( 6.8)

Якщо барабан мікрометра знаходиться праворуч від труби, а пред­мет - ліворуч від візирної осі (отже, зображення буде праворуч від візирної осі), то поправка х, як легко встановити, буде негативною:

(6.9)

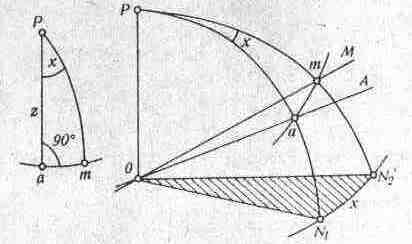
Рис. 6.10. До визначення поправки х

де М - відлік за мікрометром; - ціна поділки барабана окулярного мікрометра.Для перевірочної труби в цьому випадку поправка х₁ буде позитивною. Перевірочна труба скріплена з підставкою теодоліта; щоб візирну вісь її навести на предмет М , потрібно повернути підставку (і лімб, який знаходиться на підставці) ліворуч. Відлік за лімбом при цьому зростає. Отже, формула поправки для перевірочної труби буде такою:

(6.10)

Барабан мікрометра повинен знаходитися праворуч від труби.

Визначення ціни оберту барабана окулярного мікрометра. Ціну оберта барабана окулярного мікрометра визначають у чотири прийоми з перестановкою лімба через 45° і окулярного мікрометра - че­рез 25 поділок барабана.

Барабан встановлюють на потрібний відлік. Навідним гвинтом алі­дади трубу наближено наводять на вертикальну нитку коліматора. Потім тричі точно наводять рухомим бісектором і беруть відліки по барабану мікрометра і лімбу. Тоді ставлять барабан мікрометра на наступний відлік і вимі-рювання продовжують у тому самому порядку. Після того як закінчать вимірювання, визначають зенітальну відстань горизонтальної нитки коліматора. Позначимо через М₁, М₂, ..., М_п відліки за барабаном мікрометра, через К₁, К₂,..., К_п - відліки за лім­бом теодоліта. Далі обчислюємо для кожного прийому середні значен­ня М₀ та К₀ і утворюємо відхилення ΔМ = М₀ - М, ΔК = К₀ - К. Неважко скласти рівняння поправок:

(6.11)

Розв'язуючи його методом найменших квадратів, одержуємо ціну оберту барабана

(6.12)

Для перевірочної труби відліки К знімають з лімба коліматора, тому що кожного разу доводиться обертати барабан окулярного мік­рометра досліджуваного теодоліта й алідаду коліматора.

Польове визначення R виконують за такою самою програмою, тіль­ки замість коліматора вибирають земний предмет, відстань до якого не менше 1 км.

В оптичних теодолітах замість гвинтового мікрометра застосо­вують оптичні мікрометри.

Винайдення гвинтового мікрометра для визначення з ве-ликою точ­ністю малих відстаней було видатним досягненням у геодезії. Його винайшов у 1640 р. в Англії механік Гаскойн. Оптичний мікрометр з плоскопаралельною пластинкою винайшов німець Вільд у 1918 р. Кли­новий оптичний мікро-метр винайдено в 1923 р. Перший оптичний тео­доліт сконструйовано в 1922 р. фірмою „Карл Цейс" в Ієні.