6.3. Осьові системи і точні рівні

Вертикальна вісь теодоліта є його основною віссю, відносно якої роз­ташовані інші осі, вузли й частини інструмента (рис. 6.1, 6.2, 6.3).

У теодоліті ТТ-2"/6" сталева вісь алідади наглухо скріп-лена з підстав­кою інструмента. Алідада знаходить­ся в підвішеному стані. Є регулю­вальний пристрій (грибок). У теодоліті ОТ-02 циліндрична вісь; вона сти­кається з бічною поверхнею втулки підставки по вузькому ведучому поясу. Опорою для алідади є шарико-підшипник, розміщений біля верхнього кінця осі.

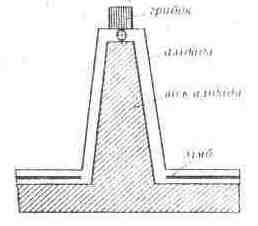
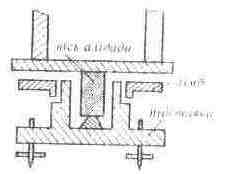
Рис.6.1. Схема осі ТТ-2"/6" Рис.6.2.Схема осей Т-1

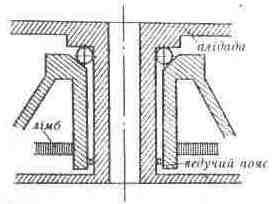
Рис.6.3.Схема осі ОТ-02

Рівні. Накладний рівень служить для вимірювання не-великих кутів нахилу і для орієнтування вертикальної осі теодоліта у прямовисне положення. Рівень при алідаді вертикального круга призначений для приведення в гори- зонтальне положення прямої, яка сполучає відліко­ві індекси алідади вертикального круга.

Високоточний рівень складається з циліндричної ампули, виготов­леної з тугоплавкого високосортного скла марок „Пірекс", „Крон", „Флінг" (рис.6.4).

Рис. 6.4. Ампула рівня

Всередині ампулу добре шліфують. Потім її запов­нюють рідиною (наркозним ефіром) і запаюють. Повітря, що є в цій рі­дині, утворює бульбашку, яка намагається зайняти верхнє положення в ампулі. Всередині ампули є камера для регулювання довжини бульбашки і компенсатор для збе-реження постійної температури рідини.

Точні рівні бувають ка­мерні і компенсаційні. Радіус кривизни внутріш­ньої поверхні ампули в точних рівнях значний. Так, в ампулі накладного рівня ТТ-2"/6" радіус кри­визни близько 206 м. Рівень має ще шка­лу, розмір найменшої поділки якої 2 мм, і оправу. Харак­теристиками рівня є ціна його поділки і чутливість. Ціною поділки рівня називається центральний кут , який відповідає найменшій поділці шкали: де r- радіус кривизни ампули; - число секунд у радіані.

Чутливість рівня - це невеликий кут, на який потрібно нахилити ампулу, щоб бульбашка почала переміщуватися.

Циліндричний рівень винайшов у 1662 р. французький механік М.Тевено.

Розглянемо, як за допомогою рівня визначають невеликі кути нахи­лу (рис. 6.5.). Положення бульбашки фіксують за її кінцями (лівим, пра­вим), роблячи відліки в поділках шкали. Нехай 0 - нуль-пункт рівня, тобто найвища точка шкали, коли підставка рівня займає горизонталь­не положення.

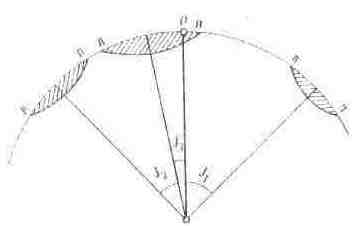
Рис. 6.5. До визначення кутів нахилу

На рисунку показано три положення підставки рівня. J₁,J₂,J₃ - кути нахилу підставки; їм відповідають три положення бульбашки. Легко встановити, що

(6.1)

Отже, якщо бульбашка рівня знаходиться далеко від нуль-пункту (перше й друге положення), то кут нахилу дорівнює сумі відліків на її кінцях, помноженій на ціну півподілки рівня. Якщо ж бульбашка перетинає нуль-пункт (третє положення), то кут нахилу дорівнює різниці відліків на її кінцях, помноженій на ціну півподілки рівня. Причому від більшого відліку треба відняти менший. У цьому неважко переконатися.

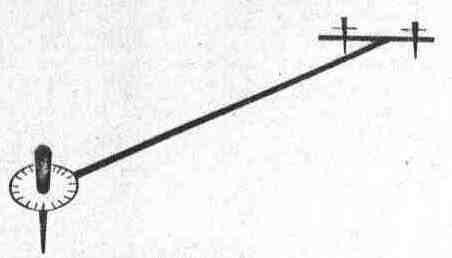
Дослідження рівнів. Високоточні рівні досліджуються на спеціальному приладі - екзаменаторі, що являє собою металеву станину Т-подібної форми. Вона складається з двох скріплених між собою балок з двома піднімальними гвинтами і мікрометра з диском поділок (рис. 6.6). Ціну поділки диска мікрометра визначають за формулою

(6.2)

Рис. 6.6. Схема екзаменатора

де d - крок гвинта мікрометра; L.- довжина балки екза-менатора; p"- число секунд у радіані.

На диску екзаменатора нанесено 100 або 120 поділок. Досліджу­ваний рівень встановлюють на станину екзамена-тора і роблять нахи­ли, обертаючи гвинт мікрометра. При цьому бульбашку рівня перега­няють з одного крайнього положення шкали рівня в друге крайнє по­ложення. Досліджують робочу частину шкали рівня.

Через однакові проміжки часу беруть відліки по диску поділок екзаменатора (при цьому лічать цілі оберти барабана мікрометра) і по шкалі рівня. Нехай у початковий момент часу t₀, відлік за екзамена­тором становить поділок, а за рівнем - х поділок шкали. У наступний момент часу t відліки були відповідно l і β. Неважко визначити кут нахилу станини екзаменатора за мікрометром екзаменатора і за шка­лою рівня.

. (6.3)

Нехай далі бульбашка рівня зміщується на z поділок за одиницю часу під впливом зовнішніх умов. За час t-t₀, вона переміститься на z(t-t₀) поділок. Позначимо через р вплив якості шліфування ампули рівня на його відліки. Тоді одержимо рівняння з чотирма невідомими:

(6.4)

Початковий відлік за рівнем x вважається також невідомим, тому що всі наступні відліки беруть через відповідний час (наприклад через 2 хв), а перший початковий відлік - інакше.

До невідомих відносять також , z і р.

При дослідженні рівнів одержуємо багато таких рівнянь. Розв'я­зуючи їх методом найменших квадратів, визначаємо невідомі, які на­дійно характеризують якість рівня.

Описаний метод дослідження рівнів на екзаменаторі запропонував у 1925 р. пулковський астроном професор А.С.Васильєв.

Метод Комстока. Ціну поділки рівня в астрономічних вимірюваннях, знаходять так. Піднімальними гвинтами відхиляють вісь обертання z теодоліта на невеликий кут І.

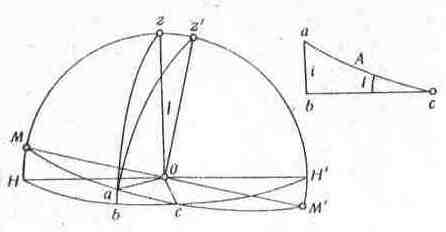
Рис. 6.7. До визначення

На рис. 6.7 НbсН' - площина гори­зонту, МaсМ'- площина, в якій знаходиться вісь рівня Оа. Коли по­вертаємо алідадну частину теодоліта, бульбашка рівня переміщується. Ми може-мо фіксувати положення кінців бульбашки рівня (нахили і) і брати відліки А за лімбом. З прямокутного сферичного трикутника abc маємо:

( 6.5)

Визначаючи невеликі зміни ΔА за лімбом і Δi за шкалою рівня, неважко, виконуючи відповідну програму вимірювань, знайти ціну по­ділки шкали рівня. Цей метод належить Комстоку.