4. Азимути Лапласа

Пункти тріангуляції, на яких є дані астрономічних вимірювань ши­роти, довготи й азимута будь-якого напрямку, називаються пунктами Лапласа. Знаючи астрономічні координати φ і λ тріангуляційного пунк­ту, астрономічний азимут α якого-небудь напрямку і геодезичну дов­готу L, можна обчислити геодезичний азимут того самого напрямку за формулою

A=α-(λ-L)sinφ. (5.17)

Азимути напрямків, обчислені за формулою (5.17), яку вперше ви­вів французький математик і астроном П. Лаплас, називають азиму­тами Лапласа. Геодезичну довготу L при цьому визначають з попе­редньої обробки тріангуляції. Визначення азимута Лапласа залежить головним чином від точності у визначенні астрономічного азимута і дещо менше - від визначення довгот.

Пункти Лапласа існують на кінцях кожної базисної сторони тріангуляції 1-го класу. Вони служать для правильного орієнтування за меридіанами і паралелями рядів тріангуляції 1 класу; для контролю куто­вих вимірювань і для підвищення точності результатів вирівнювання ланок тріангуляції 1-го класу. За азимутами Лапласа і виміряними кута­ми в ланках тріангуляції 1-го класу складають азимутальні умови рів­няння. Їх враховують при вирівнюванні разом з базисними умовними рівняннями і рівняннями фігур. Завдяки азимутам Лапласа значно зменшується поперечне зміщення ряду так само, як завдяки базис­ним сторонам зменшується поздовжнє зміщення ряду тріангуляції 1-го класу.

4. Суцільні мережі тріангуляції

Крім тріангуляції 1-го класу, будують суцільні мережі тріангуляції 2-го кла­су. При проектуванні цих обширних суцільних мереж виникає необхід­ність у попередньому обчисленні точності їхніх елементів. Тривалий час попередню оцінку точності суцільних мереж тріангуляції великої протяжності зробити було складно. Вперше це завдання в 1956 році ви­конав проф. К. Л. Проворов. Наведемо короткий зміст його дослід­жень.

Ряд тріангуляції з п рівносторонніх трикутників вивчено добре: є точні формули, за якими можна оцінити будь-який його елемент. На рис. 5.4 цей ряд знаходиться між сторонами а і а_п. Якщо до нього при­єднати рівносторонні трикутники, які мають одну або дві-спільні з ним вершини, то входить потрійний ряд з трикутників. У ньому виникають умови рівняння фігур, горизонту і полюсні (при вирівнюванні в ку- тах). Врахувавши всі ці рівняння, К. Л. Проворов виводить формули для оцінки точності потрійного ряду тріангуляції. Причому оцінюються еле­менти в початковому ряді з п три-

кутників. Потім послідовно приєдну­ють суміжні замкнуті ланцюги з рівносторонніх трикутників (при цьо­му виходять п'яти-, семикратні і т. д. ряди); кожного разу, враховуючи умовні рівняння, що виникають, виводять відповідні формули. За ними оцінюють початковий ряд аа_п. Формули, виведені з дев'ятикратного ряду, приймають для оцінки точності суцільної мережі тріангуляції. На­водимо формули К.Л.Проворова, за якими оцінюють дирекційний кут і дов-жину сторони:

( 5.18)

Рис. 5.4. Суцільна мережа тріангуляції

Значення t_n наведено в табл.5.3.

К.Л.Проворов вивів також формули, за якими визначають поз­довжнє і поперечне зміщення ряду (щодо вихідної сторони a) aa_n три­кутників, який знаходиться в сере-дині суцільної мережі з рівносторонніх трикутників:

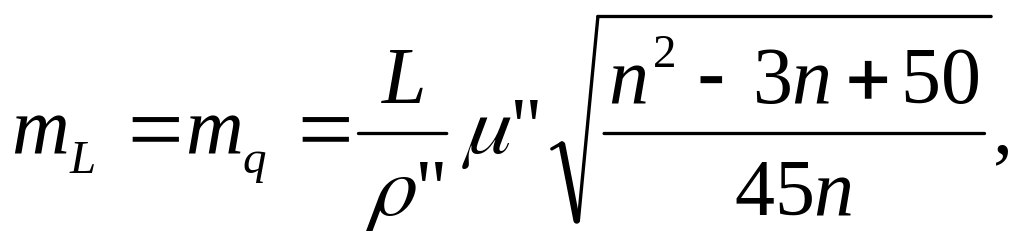
(5.19)

де n- число трикутників у початковому ряді aa_n. При цьому врахову­вались умовні рівняння фігур, горизонтів і полюсів.

Крім того, проф. К. Л. Проворов вивів аналогічні формули, врахо­вуючи уже названі умовні рівняння та рівняння дирек- ційних кутів і ба­зисів у початковому ряді, а також ряд інших формул. Одержані форму­ли можна застосовувати для оцінювання суцільних мереж тріангуляції з трикутниками довільної форми. Суцільні мережі тріангуляції можна оцінювати і за еквівалентними формулами проф. О.І. Дурнєва.

Таблиця 5.3.

_{Значення tn}

	n	tn	п	tn	п	tn	n	tn		п	tn
	1	0,457	6	0,117	11	0,022	16	0,004		16	0,004
	2	0,375	7	0,084	12	0,016	17	0,003		17	0,003
	3	0,291	8	0,060	13	0.011	18	0,002		18	0,002
	4	0,219	9	0,043	14	0,008	19	0,002		19	0,002
	5	0,161	10	0,031	15	0,006	20	0,001		20	0,001