
- •Завдання вищої геодезії. Основні поняття
- •Геометрія земного еліпсоїда
- •Розв’язування геодезичних задач
- •Опорні геодезичні мережі
- •Оцінка точності побудови опорних
- •Високоточні теодоліти і їх дослідження
- •Високоточні вимірювання горизонтальних кутів
- •Вимірювання базисів
- •Врівноваження тріангуляції, трилатерації та лінійно-кутової тріангуляції
- •Метод точної полігонометрії. Комбіновані геодезичні мережі
- •Високоточне геометричне нівелювання
- •Тригонометричне нівелювання
- •І. Завдання вищої геодезії. Основні поняття та визначення
- •1.1. Предмет і завдання вищої геодезії
- •1.2. Поняття про загальний еліпсоїд, референц-еліпсоїд, геоїд і квазігеоїд
- •1.3. Геодезичні і астрономічні координати. Відхилення виска. Вихідні геодезичні дати
- •1.4. Поняття про методи визначення фігури Землі
- •Астрономо-геодезичний метод
- •1.4.2. Гравіметричний метод
- •1.4.2.Супутниковий метод
- •2. Геометрія земного еліпсоїда
- •2.1. Параметри земного еліпсоїда, зв’язки між ними
- •2. 2. Рівняння поверхні еліпсоїда
- •Поверхню можна ще визначити з допомогою трьох рівнянь:
- •2.3. Криві на поверхні еліпсоїда
- •2.3.1. Нормальні перерізи
- •2.3.2. Геодезична лінія
- •3. Розв'язування геодезичних задач
- •3.1. Види геодезичних задач
- •3.2. Короткі історичні відомості
- •3.3.Точність розв'язування головної геодезичної задачі на поверхні еліпсоїда
- •3.4. Основні шляхи розв'язування геодезичних задач
- •3.4.1. Розв'язування сфероїдних трикутників
- •Сферичний надлишок
- •Способи розв'язування малих сфероїдних трикутників а )за формулами сферичної тригонометрії
- •Б) за теоремою Лежандра
- •В) за способом аддитаментів
- •Г) за виміряними сторонами
- •4. Опорні геодезичні мережі
- •4.1. Методи створення геодезичних мереж
- •4.1.1. Метод тріангуляції
- •4.1.2. Метод полігонометрії
- •4.1.3. Методи трилатерації та лінійно-кутової тріангуляції
- •4.2. Класифікація геодезичних мереж, їх призначення і точність
- •4.3. Основні геодезичні роботи в Росії
- •4.4. Схема та програма побудови геодезичної мережі колишнього срср
- •4.5. Загальні відомості про побудову геодезичної мережі в Німеччині, сша, Японії
- •4.6. Проектування геодезичних мереж 2-го класу
- •4.6.1. Аналітичний метод визначення висот геодезичних знаків
- •4.6.2. Проектування мереж згущення
- •1:25000, 1:10 000 1 Пункт на 50-60 км2
- •1:5 000 1 Пункт на 20-30 км2
- •4.6.3. Рекогносцировка
- •4.7. Геодезичні центри і знаки
- •4.8. Відомості про організацію основних геодезичних робіт
- •Оцінка точності побудови опорних геодезичних мереж
- •5.1. Загальні відомості про оцінку точності опорних геодезичних мереж
- •5 2. Середні квадратичні похибки передачі дирекційних кутів і довжин сторін у ряді тріангуляції
- •У цьому окремому випадку маємо одне умовне рівняння фігури
- •Найвигідніша форма трикутника в тріангуляції
- •Поздовжнє і поперечне зміщення ряду тріангуляції
- •Азимути Лапласа
- •Суцільні мережі тріангуляції
- •Оцінка точності мереж трилатерації
- •5.8. Оцінка точності мереж лінійно-кутової тріангуляції
- •6. Високоточні теодоліти та їx дослідження
- •6.1. Характерні особливості високоточних теодолітів
- •6.2. Характеристика деяких сучасних теодолітів
- •6.3. Осьові системи і точні рівні
- •6.4.Зорові труби. Окулярні мікрометри
- •6.5. Лімби теодолітів. Відлікові устаткування
- •6.6. Колімаційна похибка труби. Нахил горизонтальної та вертикальної осей теодоліта
- •6.7. Похибки поділок кругів теодоліта
- •7. Високоточні вимірювання горизонтальних кутів
- •7.1. Джерела похибок при вимірюванні кутів
- •7.2. Візирні цілі, фази. Світлова сигналізація. Кручення сигналів
- •7.3. Найвигідніший час для вимірювання горизонтальних кутів
- •7.4. Основні принципи високоточних вимірювань кутів
- •7.5. Методи високоточних кутових вимірювань та їх обробка
- •Розв'язуючи ці рівняння за методом найменших квадратів, утворимо функцію
- •7.6. Приведення виміряних напрямків до центрів геодезичних знаків
- •8. Вимірювання базисів
- •8.1. Нормальні міри, їх типи і вимоги до них
- •8.2. Базисний прилад бп-1
- •8.3. Поправки, які вводяться у довжину хорди. Виведення формул
- •8.4. Методика вимірювань з бп-1. Обробка даних
- •8.5. Вимірювання базисних сторін світловіддалемірами
- •9. Врівноваження тріангуляції, трилатерації та лінійно кутової тріангуляції
- •9.1. Загальні положення про обробку тріангуляції
- •9.2. Корелатний метод
- •9.3.Параметричний метод
- •10. Метод точної полігонометрії. Комбіновані геодезичні мережі
- •10.1. Основні принципи полігонометрії та її класифікація
- •10.2. Прилади для вимірювання кутів і ліній. Методика вимірювання.
- •10.3. Поздовжнє й поперечне зміщення в ходах полігонометрії
- •10.4.Оцінка точності кутових і лінійних вимірювань
- •11. Вискоточне геометричне нівелювання
- •11.1. Завдання високоточного нівелювання. Нівелірна мережа. Схема побудови і програма.
- •11.2. Початок відліку висот. Закріплення пунктів нівелірної мережі на місцевості
- •11.3. Високоточні нівеліри й рейки, їх дослідження
- •11.4. Методи високоточного нівелювання
- •11.5. Методика нівелювання і й іі класів
- •11.6. Врівноваження нівелірних мереж
- •11.7. Короткий історичний нарис
- •Тригонометричне нівелювання
- •Суть, призначення і виконання тригонометричного нівелювання
- •Література
- •Печенюк Олег Олександрович
Сферичний надлишок
Зі
сферичної тригонометрії відомо, що
сферичний надлишок
![]() сферичного трикутника АВС
(рис.3.2)
дорівнює площі цього трикутника, якщо
радіус сфери, на якій він розташований,
R=1.
При
сферичного трикутника АВС
(рис.3.2)
дорівнює площі цього трикутника, якщо
радіус сфери, на якій він розташований,
R=1.
При
![]() сферичний надлишок визначається формулою
сферичний надлишок визначається формулою
(![]() 3.1)
3.1)
Для
практичних обчислень
![]() сферичного трикутника будь-якого розміру
сферична тригонометрія надає формули
різного виду. Серед них:
сферичного трикутника будь-якого розміру
сферична тригонометрія надає формули
різного виду. Серед них:
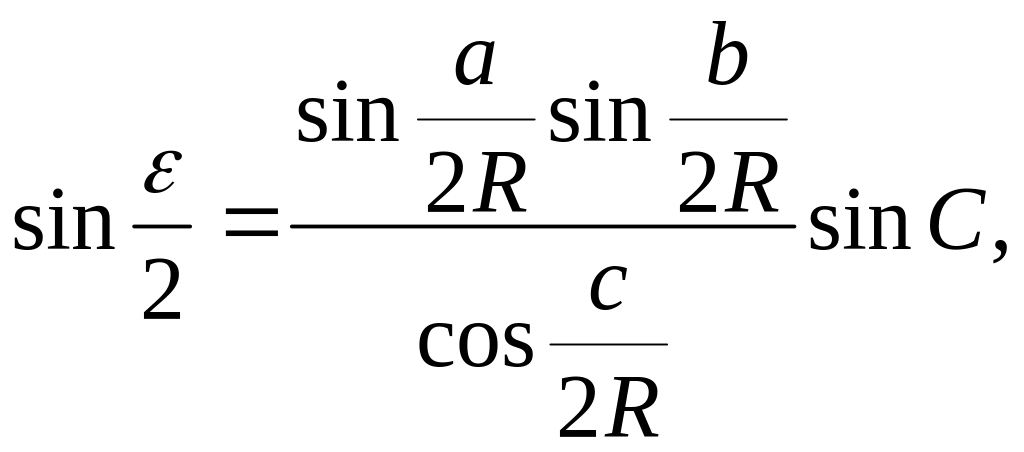
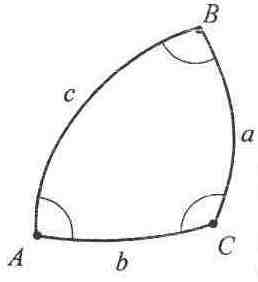
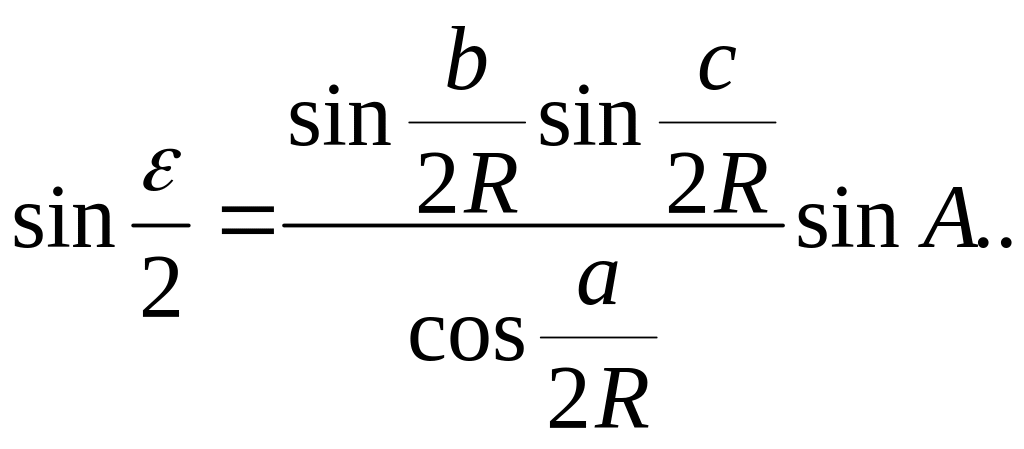
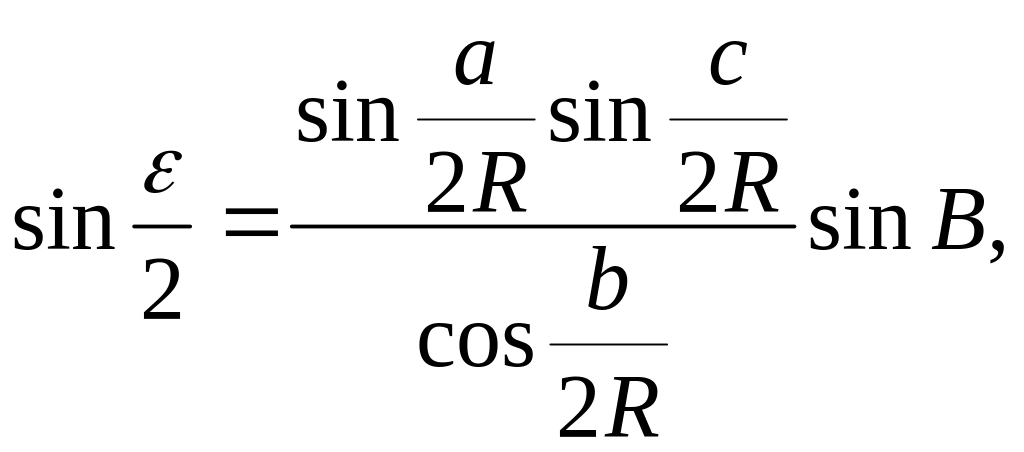
Рис.3.2
У малих сфероїдних трикутниках s«R і P«R, тому тригонометричні функції малих аргументів можна розкласти в ряди зі збереженням тільки перших членів розкладів:
![]()
В результаті отримаємо такі формули: В результаті отримаємо такі формули:
![]()
![]() (3.2)
(3.2)
![]() (3.2)
(3.2)
Для типових довжин сторін тріангуляції формули (3.2) можна використовувати без членів у дужках
(![]() 3.3)
3.3)
У випадку вимірювання всіх кутів ці формули можна перетворити так, щоб сферичний надлишок був функцією лише однієї сторони
(![]() 3.4)
3.4)
У першокласних геодезичних мережах сферичний над-лишок обчислюється з точністю до 0.001".
Для обчислення сферичного надлишку в кожному трикутнику, крім кутів, повинні бути відомі також довжини сторін. З’ясуємо, з якою точністю повинні бути відомі довжини сторін і кути, щоб обчислений за ними сферичний надлишок мав похибку не більше 0.001".
Для рівностороннього трикутника на основі формул (З.4) можемо записати
![]()
Продиференціювавши дану формулу за змінними s та β, отримаємо
![]()
![]()
Прийнявши,
що
![]() = 0.0005" та
= 0.0005" та
![]() = 60°, знайдемо допустимі похибки сторін
ds
і кутів
= 60°, знайдемо допустимі похибки сторін
ds
і кутів
![]() для різних довжин
сторін
малого сферичного трикутника (табл.
3.1). В табл. 3.1 наведено також можливі
значення сферичного надлишку
для рівносторонніх трикутників.
для різних довжин
сторін
малого сферичного трикутника (табл.
3.1). В табл. 3.1 наведено також можливі
значення сферичного надлишку
для рівносторонніх трикутників.
Одним
із основних застосувань сферичного
надлишку є
виявлення
нев'язки
![]() у
трикутнику тріангуляції
у
трикутнику тріангуляції
(![]() 3.5)
3.5)
Таблиця 3.1
s, км
|
ds, м
|
|
|
|
30 50 100
|
4 2 1
|
90 30 10
|
2 5 20
|
Способи розв'язування малих сфероїдних трикутників а )за формулами сферичної тригонометрії
Розв'язування малих сфероїдних трикутників, як було вже зазначено, зводиться до розв'язування сферичних трикутників за формулами сферичної тригонометрії. Так, для трикутника АВС (рис. 3.2), при заданій стороні а та кутах А, В, С , на основі формули синусів запишемо:
![]() (3.6)
(3.6)
![]()
де радіус сфери R визначається як функція середньої широти В, на якій розташований трикутник, за відомими формулами
![]()
Недоліком даного способу є те, що сторони трикутника виражаються в частинах радіуса, крім того, тригонометричні функції малих кутів треба знати з досить високою точністю (10-12 розрядів).
У геодезичних мережах довжини сторін трикутників, як правило, значно менші радіуса сфери. Враховуючи цей факт, формули (3.6) можна замінити іншими, більш простими в практичному плані.
