
- •1)Численные методы решения системы алгебраических уравнений
- •2)Формирование матричных уравнений состояния сети
- •3)Основные этапы решения транспортной задачи.
- •4)Метод Зейделя для ускорения решения узловых уравнений.
- •5) Узловые уравнения
- •6) Контурные уравнения.
- •8) Метод Гаусса при решении уравнений состояния сети.
- •9)Динамическая устойчивость энергосистемы, методы оценки устойчивости в «большом».
- •10)1-Я матрица инциденций,закон ома и кирхгофа в матричной форме.
- •11)План транспортной задачи(матрица перевозок) и матрица тарифов.
- •12)Методы решения узловых уравнений
- •13)Критерий Гурвица для оценки статической устойчивости.
- •14) Алгебраические критерии устойчивости.
- •16) Устойчивость состояния равновесия.
- •21) Необходимое и достаточные условия устойчивости.
- •22) Первый метод Ляпунова для оценки устойчивости нелинейных систем.
- •25)Решение нелинейных узловых уравнений итерационными методами.
6) Контурные уравнения.
Контурные
ур-ния основаны на втором з-не Кирхгофа
и з-не Ома. Применение этих ур-ний, кол-во
которых равно числу независимых контуров
 ,
обусловлено тем, что по известным токам
в хордах графа схемы замещения, число
которых равно k, можно однозначно
определить токи в ветвях дерева графа
и, тем самым – токи во всех ветвях. Таким
образом, выделяя блоки, соответствующие
ветвям дерева и хордам, можно записать
ур-ние 1-го з-на Кирхгофа в виде:
,
обусловлено тем, что по известным токам
в хордах графа схемы замещения, число
которых равно k, можно однозначно
определить токи в ветвях дерева графа
и, тем самым – токи во всех ветвях. Таким
образом, выделяя блоки, соответствующие
ветвям дерева и хордам, можно записать
ур-ние 1-го з-на Кирхгофа в виде:
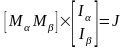 ,
где
,
где
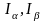 - столбцы токов в ветвях дерева и хордах
соответственно. Тогда
- столбцы токов в ветвях дерева и хордах
соответственно. Тогда
 ,
однако учитывая то, что
,
однако учитывая то, что
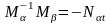 ,
тогда получим:
,
тогда получим:
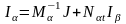 .
Учитывая это разобъем столбец I на блоки
.
Учитывая это разобъем столбец I на блоки
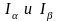 :
:
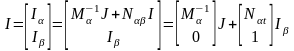 .
Поскольку при выборе системы базисных
контуров
.
Поскольку при выборе системы базисных
контуров
 ,
то
,
то
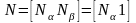 и
и
 .
Для определения тока
.
Для определения тока
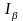 как функции параметров схемы замещения,
ЭДС в ветвях и задающих токов в узлах
воспользуемся матричным выражением
2-го з-на Кирхгофа:
как функции параметров схемы замещения,
ЭДС в ветвях и задающих токов в узлах
воспользуемся матричным выражением
2-го з-на Кирхгофа:
 .
Подставив это выражение в матрицу токов
в ветвях, получим
.
Подставив это выражение в матрицу токов
в ветвях, получим
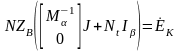 .
Таким образом, получаем систему k взаимно
независимых уравнений для определения
токов в хордах
:
.
Таким образом, получаем систему k взаимно
независимых уравнений для определения
токов в хордах
:
 .
Как известно, для системы базисных
контуров токи в хордах называются
контурными. Обозначив
.
Как известно, для системы базисных
контуров токи в хордах называются
контурными. Обозначив
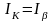 ,
получим окончательно матричное выражение
системы контурных уравнений:
,
получим окончательно матричное выражение
системы контурных уравнений:
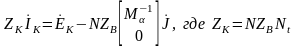 - квадратная неособенная матрица порядка
k, называемая матрицей контурных
сопротивлений.
- квадратная неособенная матрица порядка
k, называемая матрицей контурных
сопротивлений.
Решив
полученное ур-ние относительно
,
можно определить токи в ветвях дерева
схемы
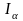 (
),
падение напряжения на ветвях схемы и
напряжения узлов относительно
балансирующего. В результате решается
задача определения параметров
установившегося режима электрической
системы.
(
),
падение напряжения на ветвях схемы и
напряжения узлов относительно
балансирующего. В результате решается
задача определения параметров
установившегося режима электрической
системы.
7)2-я матрица инциденций,2закон кирхгофа в матричной форме
Второй закон Кирхгофа определяет баланс напряжений в контурах цепи, алгебраическая сумма падений напряжения на ветвях контура равна нулю. Для произвольного контура, содержащего l ветвей, уравнение имеет вид
![]() .
(2.3)
.
(2.3)
Схема замещения электрической системы обычно является связанным направленным графом. Она состоит из ветвей (ребер), соединенных в узлы (вершины). Ветви образуют цепочки (пути графа), которые могут быть замкнутыми. Все величины, характеризующие состояние ветвей (ЭДС, токи, падения напряжения), имеют определенное направление.
Для направленного графа могут быть определены: 1) матрица соединений ветвей в узлах (первая матрица инциденций); 2) матрица соединений ветвей в независимые контуры (вторая матрица инциденций).
Матрица соединений ветвей в узлах – это прямоугольная матрица, число строк которой равно числу вершин графа n, а число столбцов – числу ребер m.
M =(mij), i=1,...,n; j=1,....,m..
Матрица соединений ветвей в независимые контуры – это прямоугольная матрица, число строк которой равно числу независимых контуров графа k, а число столбцов – числу ветвей m.
N=(nij), i=1,……..k; j=1,……. m.
Матрицы М и N дают возможность записать уравнения состояния электрической цепи в матричной форме.
Второй закон Кирхгофа в матричной форме
(2.5)
где - столбец падений напряжений на ветвях схемы.
