Вопросы по дисциплине «Математические задачи энергетики и компьютерное моделирование»
(часть 3)
Моделирование. Физические и математические модели. Компьютерное моделирование.
Моделирование. Аналитическое и имитационное моделирование.
Этапы математического моделирования.
Концептуальная модель обобщенного электромеханического преобразователя. Формализация модели.
Формализация математической модели на примере обобщенного электромеханического преобразователя.
Программная реализация математической модели.
Аналитическое решение дифференциальных уравнений математической модели обобщенного электромеханического преобразователя.
Численное решение дифференциальных уравнений математической модели обобщенного электромеханического преобразователя.
Решение дифференциальных уравнений математической модели обобщенного электромеханического преобразователя методом Эйлера.
Решение дифференциальных уравнений математической модели обобщенного электромеханического преобразователя модифицированным методом Эйлера.
Решение дифференциальных уравнений математической модели обобщенного электромеханического преобразователя методом Рунге –Кутта 4-го порядка.
Решение систем дифференциальных уравнений математической модели обобщенного электромеханического преобразователя модифицированным методом Эйлера.
Решение систем дифференциальных уравнений математической модели обобщенного электромеханического преобразователя методом Рунге – Кутта 4-го порядка.
Применение встроенных функций компьютерных математических приложений для решения дифференциальных уравнений математических моделей.
Применение встроенных функций компьютерных математических приложений для решения дифференциальных уравнений математических моделей.
Применение встроенных функций компьютерных математических приложений для решения систем дифференциальных уравнений математических моделей.
Имитационное моделирование. Область применения.
Имитационное моделирование. Виды имитационных экспериментов.
Имитационное моделирование. Особенности компьютерных систем имитационного моделирования.
Обработка результатов эксперимента. Интерполяция и экстраполяция.
Обработка результатов эксперимента. Аппроксимация.
Обработка результатов эксперимента. Одномерная линейная интерполяция.
Обработка результатов эксперимента. Одномерная сплайн – интерполяция и аппроксимация.
Обработка результатов эксперимента. Регрессии. Выполнение линейной регрессии.
25. Задачи гармонического анализа и синтеза.
Часть 1
Что понимается под энергосистемой?
Режим энергосистемы это:
Параметры режима
Переходный режим
Расчетная модель системы
Что такое узел схемы?
Что такое ветвь схемы?
Для чего вводится балансирующий узел?
Граф системы
Первая матрица инцеденций -эта
Вторая матрица инциденций-это
Для чего используется первая матрица инцеденций?
Для чего используется вторая матрица инцеденций?
Разомкнутая схема
Методы решения линейных уравнений установившихся режимов.
Методы решения нелинейных уравнений
?Независимые переменные при решении матричных узловых уравнений
Суть метода Гаусса
?Суть итерационных методов
?Какие задачи решаются методом линейного программирования?
Необходимые и достаточные условия статической устойчивости
Критерий Гурвица
Суть метода последовательных интервалов
Статическая устойчивость
Динамическая устойчивость
?Первый метод Ляпунова
Второй метод Ляпунова
Устойчивость состояния равновесия
Что такое возмущение
Часть 1 Оржанова
1 Математические модели элементов энергосистемы, модели используемая при расчетах параметров системы.
2 Математические модели установившихся и переходных режимов энергосистемы, модели используемая для моделирования работы системы
3 Аналитическое представление конфигурации сети.
4 Первая матрица инцеденций, закон Ома и Кирхгофа в матричной форме.
5 Вторая матрица инцеденций, второй закон Кирхгофа в матричной форме.
6 Метод Гаусса при решении уравнений состояния сети
7 Метод Зейделя для ускорения решения узловых уравнений.
8 Решение нелинейных узловых уравнений итерационными методами.
9 Методы решения узловых уравнений.
10 Формирования матричных уравнений состояния сети.
11 Узловые уравнения.
12 Контурные уравнения.
13 Устойчивость состояния равновесия.
14 Статическая устойчивость энергосистемы, методы оценки устойчивости в «малом»
15 Динамическая устойчивость энергосистемы, методы оценки устойчивости в" большом»
16 Необходиме и достаточные условия устойчивости
17 Алгебраические критерии устойчивости
18 Критерии Гурвица для оценки статической устойчивости.
19 Метод Д-разбиения .
20 Первый метод Ляпунова для оценки устойчивости нелинейных систем.
21 Второй метод Ляпунова для оценки устойчивости в «большом».
22 Математическая постановка задачи линейного программирования.
23 Поставка транспортной задачи в матричной форме.
24 План транспортной задачи(матрица перевозок) и матрица тарифов.
25 Основные этапы решения транспортной задачи.
26 Определение исходного опорного плана
27 Решение транспортной задачи методом потенциалов.
28 Решение транспортной задачи с открытой моделью.
29 Численныеметоды решения систем алгебраических уравнений.
30 Метод последовательных интервалов для исследования переходных процессов
Схемы замещения электрических систем, по своей сути, являются:
Схема замещения с соответствующими формулами, уравнениями их расчета можно назвать:
Идеальный источник напряжения обладает способностью:
Идеальным источником напряжения называют источник ЭДС, который имеет:
Количественное определение идеального источника напряжения можно определить выражением:
Идеальный источник тока обладает способностью:
Идеальным источником тока называют источник ЭДС, который имеет:
Количественное определение идеального источника тока можно определить выражением:
Напряжение реального источника напряжения определяется по формуле:
Реальный источника напряжения можно описать через источник тока по следующей формуле:
Ток реального источника тока определяется по формуле:
Реальный источника тока можно описать через источник ЭДС по следующей формуле:
Величина тока для реального источника ЭДС с внутренним сопротивлением
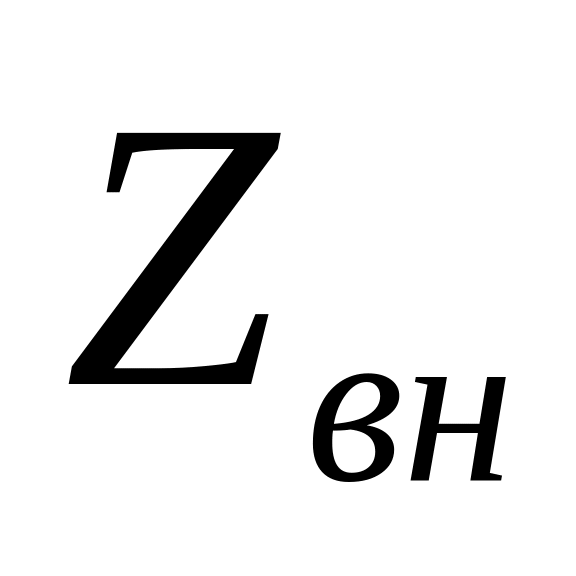и нагрузкой
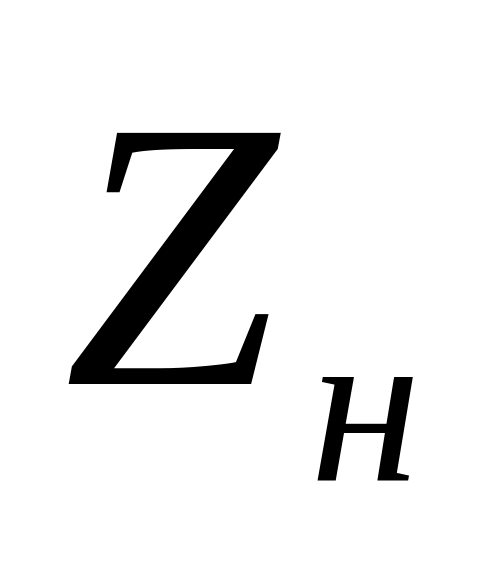определяется по формуле:Если к реальному источнику ЭДС с внутренним сопротивлением подключена нагрузка , то отклонение выходное напряжение определяется по формуле:
Если реальный источник ЭДС с внутренним сопротивлением заменить источником тока, то величина тока источника определяется по формуле:
Если реальному источнику тока с внутренним сопротивлением подключена нагрузка , то величина напряжения определяется по формуле:
Если реальному источнику тока с внутренним сопротивлением подключена нагрузка , то величина напряжения определяется по формуле:
Слово «активный» применительно к сопротивлению имеет следующий смысл:
Какой эффект воспринимается за «реактивное» сопротивление:
Индуктивная проводимость определяется выражением:
Емкостная проводимость определяется выражением:
Трансформатором называется устройство, которое:
Идеальный трансформатор характеризуется:
Уравнения идеального трансформатора имеют вид:
Для идеального трансформатора верно следующее выражение:
Реальный трансформатор отличается тем, что:
Уравнения описывающие принцип работы воздушных линий можно представить в следующем виде:
Уравнения напряжение, обусловленное взаимондукцией воздушных линий можно представить в следующем виде:
Под понятием прочной нагрузки понимают:
Под эквивалентированием нагрузки понимают: