1.2 Калибровка температурной шкалы с учетом термического запаздывания

Калибровкой называют набор операций, проведенных в определенных условиях и

устанавливающих связь между измеренным значением некоторой величины и соответствующим значением данной величины, точно известным для стандартов. В ДСК

величинами, значения которых измеряются, являются тепловой поток, теплота и температура [2].

В табл. 1.2.1 приведены равновесные температуры плавления , некоторых эталонных материалов, используемых в ДСК для калибровки температурной шкалы. Температурный интервал превращений в указанных эталонах перекрывает почти весь рабочий диапазон приборов ДСК. При отсутствии термического запаздывания, т.е. в квазиравновесных условиях испытания (ν→0), точность калибровки температурной шкалы определяется точностью прибора и составляет, например, у DSC-2 величину ±0,1 К. В динамических условиях испытания (ν≠0) для реализации близкой точности необходимо проводить калибровку температурной шкалы с учетом термического запаздывания [2].

Рассмотрим здесь этот вопрос применительно к истинному фазовому переходу I рода — плавлению, когда смещение и изменение формы эндотермического пика плавления при изменении условий опыта могут иметь только чисто методическую причину. В отличие от суммарного теплового эффекта ∆q равного ∆H, вне зависимости от условий испытания и скорости нагревания, температура максимума эндотермы плавления , всегда отличается от истинной температуры плавления . Обусловлено это наличием термического сопротивления R, которое приводит к термическому запаздыванию — отставанию температуры образца от температуры нагревателя на величину ∆Т=Т_max- . При плавлении чистых веществ ошибка ∆Т пропорциональна скорости нагревания v, удельной теплоте плавления массе образца m и термическому сопротивлению R:

∆T=(2m·∆H_пл·Rν)^1/2 (1.2.1)

Видно, что при постоянном R и образцах одинаковой массы ожидается линейная зависимость ∆Т(ν^1/2) . При v→0 разность ∆Т→0 и T_max→ .

Таблица 1.2.1. Эталоны для калибровки, используемые в ДСК [2, c. 13].

Следовательно, экстраполяция линейной зависимости Т_max(ν^1/2) к нулевой на скорости нагревания дает значение [2].

На рис 1.2.2 в качестве примера представлены зависимости температур максимумов эндотермических пиков плавления от ν^1/2 для эталона индия. Видно, что экспериментальные точки для Т_max ложатся на прямые (1 и 2), а экстраполяция их к нулевой скорости нагревания, при соответствующей настройке температурной шкалы прибора, дает истинную, равновесную температуру плавления „= =429,8 К. Увеличение массы образца приводит, в соответст- вии с уравнением (1.2.1), к увеличению наклона линейной зависимости Т_max(ν^1/2), т. е. ∆Т(ν^1/2) [2].

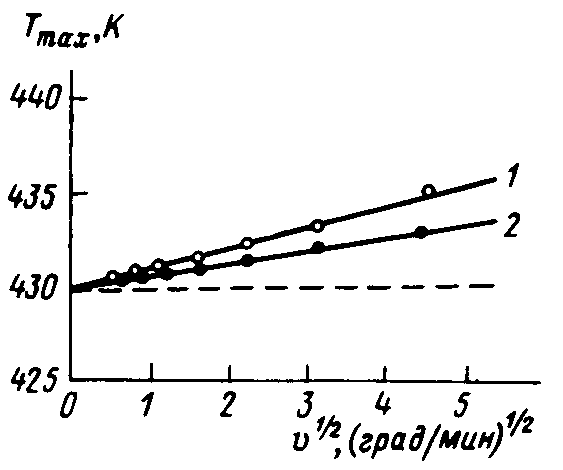
Рис. 1.2.2. Зависимости Т_max пика плавления от скорости нагревания образцов индия разной массы (1=5.2 мг. и 2=1.6 мг.) [2, с. 14].

Точность калибровки температурной шкалы при учете термического запаздывания зависит от точности экстраполяции линейной зависимости ∆Т(ν^1/2) и, в общем случае, снижается в сравнении с точностью прибора. Она зависит от числа реперных точек и при использовании широкого набора скоростей нагревания составляет ± 0,2 К [2].

В том случае, когда интерес представляет только температура а форма эндотермического пика имеет второстепенное значение, описан- ный способ температурной калибровки прибора существенно облегчает учет термического запаздывания и определение истинной температуры плавления [2].

Расчет по уравнению (1.2.1) величины ∆Т при соответствующей экспе- рименту скорости нагревания ν, известных m, ∆Н_пл и R (об определении R см. ниже) и вычитание этой величины из экспериментально найденного при одной скорости нагревания значения Т_max; определение , путем экстраполяции экспериментальной зависимо- сти Т_max(ν^1/2) к нулевой скорости нагревания [2].