- •1. Особенности математических понятий. Объем и содержание понятия. Определение понятий. Структура определения понятия через род и видовое отличие.
- •3. Понятие бинарного отношения между элементами одного множества. Способы задания отношений. Свойства отношений.
- •4. Отношение эквивалентности и его связь с разбиением множества на попарно-непересекающиеся подмножества или классы. Отношение порядка, его виды.
- •5. Понятие соответствия между элементами двух множеств. Способы задания соответствий. Соответствие обратное данному. Взаимно-однозначные соответствия. Равномощные множества
- •6. Определение числовой функции. Способы задания функции. Прямая пропорциональность, ее свойства и график.
- •7. Определение числовой функции. Способы задания функции. Обратная пропорциональность, ее свойства и график.
- •8. Тмс натурального числа и нуля
- •9. Теоретико-множественный смысл суммы целых неотрицательных чисел. Законы сложения
- •10. Теоретико-множественный смысл разности целых неотрицательных чисел. Определение разности через сумму. Теорема о существовании разности.
- •11. Правила вычитания числа из суммы и суммы из числа (теоретико-множественная интерпретация) Правило вычитания числа из суммы
- •Правило вычитания суммы из числа
- •12. Определение произведения целых неотрицательных чисел, его теоретико-множественный смысл. Законы умножения.
- •13. Дистрибутивные (распределительные) законы умножения относительно сложения и вычитания целых неотрицательных чисел. Закон умножения относительно вычитания
- •14. Теоретико-множественный смысл частного целого неотрицательного числа и натурального. Определение частного через произведение. Условие существования частного.
- •Два типа задач
- •2)Деление на равные части:
- •15. Определение частного через произведение. Невозможность деления на нуль (с доказательством).
- •16. Правила деления суммы на число и числа на произведение (доказательство или теоретико-множественная интерпретация одного из них) Правила деления
- •Правила деления числа на произведение
- •17. Теоретико-множественный смысл деления с остатком на множестве целых неотрицательных чисел.
- •18. Понятие числового выражения, числового равенства и неравенства. Основные свойства истинных числовых равенств и неравенств.
- •19. Понятие выражения с переменной и уравнения с одной переменной. Равносильные уравнения. Теоремы о равносильности уравнений.
- •20. Позиционные и непозиционные системы счисления. Особенности десятичной системы счисления. Сравнение чисел в десятичной системе счисления.
- •21. Алгоритм сложения многозначных чисел, теоретические положения, лежащие в его основе
- •22. Алгоритм вычитания многозначных чисел, теоретические положения, лежащие в его основе.
- •23. Алгоритм умножения многозначных чисел, теоретические положения, лежащие в его основе.
- •24. Натуральное число как результат измерения величин. Смысл сложения и умножения натуральных чисел, полученных в результате измерения величин.
- •Сложение
- •Умножение
- •25. Натуральное число как результат измерения величин. Смысл вычитания и деления натуральных чисел, полученных в результате измерения величин.
- •Вычитание
- •Деление
- •26. Понятие длины отрезка и ее измерения. Свойства длины отрезков.
- •27. Понятия площади плоской фигуры и ее измерения. Свойства численных значений площадей. Равновеликие фигуры.
- •28. Понятие дроби и положительного рационального числа.
6. Определение числовой функции. Способы задания функции. Прямая пропорциональность, ее свойства и график.
Числовой функцией называется соответствие между числовым множеством Х и множеством R (действительные числа), при котором каждому числу из множества Х сопоставляется единственное число из множества R.
Множество x называется областью определения функции.
Функцию принято обозначать: f, ƒ, Ψ, y
y = ƒ(x) показывает, что x и y находятся в функциональной зависимости.
x – независимая переменная (аргумент)
y – зависит от переменной (функция)
Функцию можно задать разными способами:
1) Аналитический (т.е. при помощи формулы)
2) Табличный
Таблица – ряду значений аргумента указывается ряд соответствующих значению функций.
3) Графический (т.е. функция задается при помощи графика)
График функции – множество точек координатной плоскости, абсцисса которых – значение аргумента, взятое из области определения, а ордината – значение функции от данного значения аргумента.
Прямой пропорциональностью называется функция, которая может быть задана при помощи формулы у = kx, где k – любое действительное число, отличное от нуля.
Графиком явл. прямая линия, проходящая через начало координат.
Возможны 2 случая:

1) k > 0 y = 2x
2) k < 0 y = -2x
Свойства:
1) Область определения множества (D(f)) – любое действ. число (R) (от- беск., до +беск.)
2) область значения (Е(х)) – все действительные числа (R) (от- беск., до +беск.)
3) При к<0 функция убывает на всей области определения. При к>0 функция возрастает на всей области определения.
4) отношение двух значений аргумента равно отношению соответственных значений функции, т.е. х1 : х2 = у1 : у2.
Если х и у – положительные числа, то с увеличением значения переменной х в несколько раз соответствующие значения функция возрастает во столько же раз.
7. Определение числовой функции. Способы задания функции. Обратная пропорциональность, ее свойства и график.
Числовой функцией называется соответствие между числовым множеством Х и множеством R (действительные числа), при котором каждому числу из множества Х сопоставляется единственное число из множества R.
Множество x называется областью определения функции.
Функцию принято обозначать: f, ƒ, Ψ, y
y = ƒ(x) показывает, что x и y находятся в функциональной зависимости.
x – независимая переменная (аргумент)
y – зависит от переменной (функция)
Функцию можно задать разными способами:
1) Аналитический (т.е. при помощи формулы)
2) Табличный
Таблица – ряду значений аргумента указывается ряд соответствующих значению функций.
3) Графический (т.е. функция задается при помощи графика)
График функции – множество точек координатной плоскости, абсцисса которых – значение аргумента, взятое из области определения, а ордината – значение функции от данного значения аргумента.
Обратная пропорциональность
Функция, которую
можно задать формулой y
=
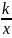 ,
где k
– любое действительное число, отличное
от нуля, называется обратной
пропорциональностью.
,
где k
– любое действительное число, отличное
от нуля, называется обратной
пропорциональностью.
Графиком функции является гипербола.
Например:
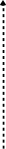
k
> 0 y
=