26. Понятие длины отрезка и ее измерения. Свойства длины отрезков.

Отрезком называется часть прямой ограниченная с двух сторон.

Длиной отрезка называется положительная величина, обладающая следующими свойствами:  1. Если отрезки равны, то равны и их длины. 2. Если отрезок состоит из 2х отрезков, то его длина равна сумме длин этих отрезков.

"Состоять из" означает: 1. Не какие два отрезка не имеют внутренних точек, но могут иметь общие концы.  2. Объединение всех отрезков равно данному отрезку.

Для того, чтобы измерить длину отрезка, нужно иметь единицу длины. Единица длины – это длина произвольно выбранного отрезка, который принимается за единичный.

В результате измерения длины отрезка мы получим положительное действительное число, которое называется численным значением или мерой длины отрезка а при выбранной единице длинны Е.

m_E (a) > 0

Рассмотрим свойства численных значений длин отрезков: 1. Если отрезки равны, то равны численные значения его длин при одной и той же единице длины.

a = b = m_E(a) = m_E(b)

Верно и обратное утверждение: Если численные значения длин отрезков равны, то равны и сами отрезки. 

2. Если отрезок a состоит из двух отрезков b и c,

a=b(+)c

то численное значение длины отрезка a, равно сумме численных значений отрезков b и c при одной и той же единице длины. 

Верно и обратное утверждение.

a=b(+)c  m_E(a) = m_E(b) + m_E(c)

Если численное значение длины отрезка a равно сумме численных значений длин отрезков b и c при одной и той же единицы длины, то отрезок a состоит из отрезков b и c. 

3. При замене единицы длины численное значение длины отрезка a увеличивается (уменьшается) во столько раз, во сколько новая единица длины меньше (больше) старой.

Например: а=5см

Е= 1см m_см (а)=5

E= 1мм

Е₁< Е в 10р.

А= 50мм Е_мм (а)=50

50>5 в 10 раз

27. Понятия площади плоской фигуры и ее измерения. Свойства численных значений площадей. Равновеликие фигуры.

Площадью фигуры называется неотрицательная величина, определенная для каждой фигуры так, что:

1) равные фигуры имеют равные площади,

2) если фигура состоит из 2-х частей, то ее площадь равна сумме площадей этих частей.

«Состоять из» означает:

1) никакие 2 фигуры не имеют общих точек, но могут иметь общее границы

2) объединение всех фигур равно данной фигуре.

Для того, чтобы измерить площадь фигуры необходимо выбрать единицу площади.

За единицу площади берут площадь квадрата со стороной, равной единичному отрезку.

В результате измерения площади фигуры получают неотрицательное действительное число, которое называется численным значением или мерой площади фигуры F при выбранной единицы площади.

S_E(F)

Рассмотрим основные свойства численных значений площадей.

1) Если фигуры равны, то равны и численные значения их площадей

F₁ 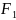= 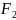F₂ => S_E(F₁) + S_E(F₂ ) при одной и той же единице площади.

Обратное утверждение выполняется не всегда

2) Если фигура F состоит из фигур F₁ и F₂, то численное значение площади фигуры E равно:

S_E(F) = S_E(F₁) + S_E(F₂) при одной и той же единице площади.

3) При замене ед. площади численное значение площади фигуры увеличивается (уменьшается) во сколько раз, во сколько новая ед. площади меньше (больше) старой.

S фигуры F = 5cм²

S_см²(F) = 5

Е = 1см²

E₁ = 1мм²

1см² = 100мм² => S_мм²(F) = 500

E₁ < E в 100 р. 500 > 5 в 100 р.

2 многоугольника называются равносоставленными, если их можно разбить на соответственно равные части.

*Фигуры называются равными, если при наложении они совпадают.

Фигуры, у которых площади равны, называются равновеликими.

Если фигуры равны, то они равновеликие.

Очевидно, что равносоставные фигуры являются равновеликими.

Равные  Равновеликие  Равносоставные

Венгерский математик Бойл и немецкий математик Гервин доказали теорему, что любые 2 равновеликих многоугольника являются равносоставными.

8 S прямоуг. = 8*4 = 32 (см2)

S треуг. = ½ 8*8 = 32

8 =>

прямоуг. и треуг. – равновеликие.

На рисунке мы видим, что прямоугольник и треугольник являются равновеликими и равносоставными, т.к. состоят из трапеции и 2-х равных треугольников.