21. Алгоритм сложения многозначных чисел, теоретические положения, лежащие в его основе

Если числа a и b однозначные, то, чтобы найти их сумму, достаточно подсчитать число элементов объединения двух непересекающихся множеств a и b таких, что n(A)=a, n(B)=b. Но, чтобы каждый раз не прибегать к такому способу, все получаемые результаты записывают в таблицу сложения однозначных чисел и запоминают ее.

Если числа a и b многозначные, то их складывают письменно, записывая пример в столбиках.

Рассмотрим, какие теоретические положения лежат в основе алгоритма сложения многозначных чисел, на конкретном примере:

- Найдем сумму чисел:

348+426 =

- Представим каждое число суммой степеней числа 10 с коэффициентами:

= 348+426=3* +4*10+8+4* +2*10+6 =

- По переместительному свойству сложения поменяем слагаемые местами:

= 3* +4* +4*10+2*10+8+6 =

- По сочетательному свойству сложения сгруппируем слагаемые:

= (3* +4*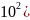 +(4*10+2*10)+(8+6) =

- По распределительному закону умножения относительно сложения вынесем степень числа 10 за скобку:

= (3+4)* +(4+2)*10+(8+6) =

- Мы видим, что сложение многозначных чисел сводится к сложению однозначных чисел, но записанных цифрами соответствующих разрядов.

- Найдем сумму по таблице сложения. Получаем:

= 7* +6*10+14

- Данная запись не является способом записи чисел в ДСС, так как не один коэффициент не может быть больше 9. Выполним дополнительные преобразования: представим число 14 суммой разрядных слагаемых:

= 7* +6*10+14=7* +6*10+(1*10+4) =

- По сочетательному свойству сложения перегруппируем слагаемые:

= 7* +(6*10+1*10)+4=7* +(6+1)*10+4 =

- По распределительному закону сложения вынесем 10 за скобку:

= 7* +7*10+4 = 774

Таким образом, в основе алгоритма сложения многозначных чисел лежат следующие теоретические положения:

1. Способ запоминания чисел в ДСС

2. Переместительное свойство сложения

3. Сочетательное свойство сложения

4. Распределительный закон умножения относительно сложения

5. Таблица сложения однозначных чисел

Алгоритм сложения сводится к следующему:

• Пишу 2-е слагаемое под 1-м так, чтобы соответствующие разряды находились друг под другом;

• Складываем однозначные числа, записываем цифрами соответствующий разряд начиная с разряда единиц;

• Если сумма однозначных чисел не больше 9, то результат подписываем под соответствующим разрядом

• Если сумма больше 9, то полученное число представляем как 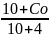(С₀ – однозначное число, которое подписывается под соответствующим разрядом. А 10 – это единица следующего разряда, которую прибавляем к единицам следующего разряда.

• Сложение заканчивается после того, как сложены единицы старших разрядов.

22. Алгоритм вычитания многозначных чисел, теоретические положения, лежащие в его основе.

Если числа а и b однозначные, то при условии, что а больше либо равно b, то, чтобы найти разность чисел а и b, достаточно подсчитать число элементов дополнения множества В до множества А таких, что n(A)=a, n(B)=b и В – подмножество А.

Но, чтобы каждый раз не прибегать к такому способу, можно использовать знание таблицы сложения однозначных чисел.

Если число а и b многозначные, то их разность находят письменно, записывая пример в столбик.

Рассмотрим, какие тп лежат в основе вычитания многозначных чисел, на конкретном примере:

648-236 =

- Представим каждое число суммой степеней числа 10 с коэффициентами:

= (6*10 ²+ 4*10+8) - (2*10²+3*10+6) =

- По правилу вычитания суммы из числа вычтем каждое слагаемое последовательно (одно за другим):

= (6*10²+ 4*10+8) - 2 *10² - 3*10 - 6 =

- По правилу вычитания числа из суммы вычтем каждое число из одного из слагаемых суммы:

= (6*10 ² - 2*10² )+(4*10 - 3*10)+(8-6) =

- По распределительному закону умножения относительно вычитания вынесем степень числа 10 за скобку:

= (6-2)*10 ² +(4-3)*10+(8-6) =

- Мы видим, что вычитание многозначных чисел сводится к вычитанию однозначных чисел, записанных цифрами соответствующих разрядов.

- Найдем разность по таблице сложения:

= 4*10 ² +1*10+2 = 412

- Получили запись числа 412 в ДСС.

Мы рассмотрели случай вычитания без перехода через разряд.

Рассмотрим случай вычитания с переходом через разряд.

642-236 =

- Мы видим, что из 2х единиц мы не можем вычесть 6 ед., поэтому выполним преобразования:

- Представим число 642 суммой степеней числа 10 с коэффициентом: = 6*10 ²+ 4*10+2 =

- Представим 4*10 как 3*10 + 1*10

= 6*10 ²+(3*10 + 1*10)+2 =

- По сочетательному свойству сложения перегруппируем слагаемые

= 6*10 ²+3*10 +(1*10+2) = 6*10 ²+3*10 +12 =

- Теперь мы из 12 можем вычесть 6 и выполнить дальнейшие вычисления, как было записано выше.

Таким образом, в основе алгоритма письменного вычитания лежат следующие теоритические положения:

1. Способ записи чисел в ДСС

2. Правило вычитания суммы из числа

3. Правило вычитания числа из суммы

4. Распределительный закон умножения относительно вычитания

5. Таблица сложений однозначных чисел

6. Сочетательное свойство сложения

Алгоритм вычитания сводится к следующему:

Пишу вычитаемое под уменьшаемым так, чтобы соответствующие разряды находились друг под другом. Вычитаем однозначные числа, записанные цифрами соответствующих разрядов, начиная с разряда единиц.

Если разность найти можно (a больше или равно b), то разность записываем под соответствующим разрядом.

Если разность найти нельзя (a меньше b), то берем единицу из следующего разряда, отличную от 0, если цифра следующего разряда равна 0, то идем влево до следующего разряда, цифра которого отлична от 0 и берем там 1единицу. Чтобы не забыть, ставим точку над цифрой. Затем возвращаемся в разряд, где вычитаем, при этом все 0 становятся 9.

Вычитание заканчивается, когда вычтем единицы старшего разряда.