Вопрос 7 Модели, построенные с применением методов регрессионного анализа. .

Статистические методы – это совокупность способов сбора, анализа и интерпретации данных о свойствах объекта или совокупности объектов с целью получения теоретических или практических выводов.

Сущность статистических методов заключается в следующем. На основе эмпирических представлений о свойствах исследуемого объекта и в соответствии с целью исследования определяется состав и тип входных параметров х₁,…х_n и перечень выходных характеристик y₁,…y_m. Затем проводится эксперимент, целью которого является получение достаточно большой выборки связей между входными параметрами и выходными характеристиками объектов. Естественно полученные в результате эксперимента данные являются случайными числами. На основании этой выборки выбирается тип статистической модели (математические выражения, структура) и рассчитываются параметры модели.

Математическая статистика предлагает обширный набор моделей и методов установления статистических закономерностей, присущих исследуемым объектам. Наиболее распространённым из них является регрессионный анализ.

1)

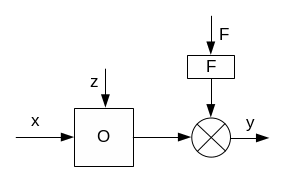
y=f(x,z,F) – Случайная модель в которой переход из одного состояния в другое происходит в случайные моменты времени и непредсказуемы

2)

y=f(x,z)+ε – детерминированный автомат, однозначно описываемый функцией, но имеются ошибки учитывающие влияние F «-» доказать адекватность можно только испытав в реальных условиях.

3)

y=f(x)+ε – учитывают только управляющие воздействия «-» недостаточно точна не учитывает внешние воздействия «+» можно испытать в лаборатории

Основная – вторая модель!

Модели объектов учитывают целенаправленные управляющие воздействия исполнительных устройств и контролируемые воздействия окружающей среды. Неконтролируемые воздействия окружающей среды приводят к появлению ошибок (в модели указываются в виде шума ). Уравнение, связывающее входные переменные с выходными, выглядит следующим образом:

y=f(x₁,…,x_k,b_1,…,b_k)+ (1),

где x_i–i-тая входная переменная,

b_i – i-тый параметр регрессионного уравнения, i=1..k.

Если функция f(x₁,…,x_k,b_1,…,b_k) линейна относительно искомых параметров b_1,…,b_k, она может быть представлена в следующем виде:

f(x₁,…x_k,b₁,…b_k)= φ_i (x), (2)

где _I(x) – некоторая заданная функция от х_i, i=1..k .

Для удобства обычно принимают ₁=1.

Чаще всего регрессионное уравнение представляют в виде степенного полинома конечной степени:

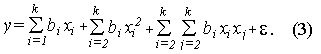
Введём фиктивные переменные: х₁=1, х²_k+1=x_k+1,…, x²_k=x_2k-1, x₂x₃=x_2k,…

В этом случае уравнение регрессии будет иметь следующий вид:

Вопрос 8 Нахождение коэффициентов регрессионного уравнения.

Точное значение коэффициентов b_i регрессионного уравнения возможно только при бесконечно большом объёме выборки. Поэтому при ограниченном объёме выборки определяют оценки этих коэффициентов _i. Исследуемое выражение будет иметь следующий вид:

где β_i – оценка математического ожидания, х₁=1.

Для определения коэф β_i проводится N эксперементов в каждом из которых измеряются все вх и вых переменные.

_I – находим по выборке, используя метод наименьших квадратов.

Функция наименьших квадратов имеет следующий вид:

где _j – экспериментальное значение выходной величины в j-том эксперименте, x_ij – значение i-той входной переменной в в j-том эксперименте. m – число слагаемых, N – Число эспериментов.

Нужно найти минимум I, тогда найдём коэфф.

В данном выражении неизвестными являются коэффициенты _i. Рассматривая эти коэффициенты как независимые переменные, и приравняв к нулю частные производные от I по _i , получим m уравнений с m неизвестными, решив которые и найдём эти коэффициенты.

Берем производную чтобы найти β_i

-расчетное значение

y – фактическое значение

- вх переменные которые использовались при эесперименте

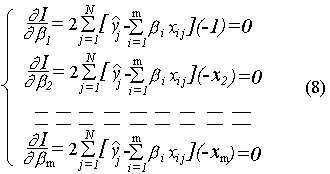
Пример 1. Определим зависимость основного удельного сопротивления движению отцепа от температуры. Результаты эксперимента с наиболее лёгким отцепом (22 тонны).

Удельное сопротивление движению wo	Температура наружного воздуха, оС
	Выше 0	-5	-15	-25	-35
	2,56	4,20	3,58	4,27	4,33

Пусть регрессионное уравнение имеет вид: w_o=₁+₂t+₃t².

В результате дифференцирования этого уравнения по _i получим три линейных уравнения, решив которые и найдём искомые коэффициенты.

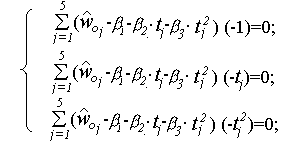
Решив эту систему уравнений, получим следующую зависимость удельного сопротивления движения отцепа от температуры:

w_o(t)= 3.133 - 0,061 t – 7.3510^-4 t²

Удельное сопротивление движению wo	Температура наружного воздуха
	Выше 0	-5	-15	-25	-35
	3.133	3.417	3.91	4.199	4.368