1. Оценка – мера дефицитности ресурсов и продукции.

Неиспользованный полностью в оптимальном плане ресурс имеет (у_i*=0) –недефицитный (невыгодно использовать его полностью). Ограничивают целевую функцию дефицитные ресурсы. Дефицитность продукции: нулевую оценку получает продукция, выпуск которой в оптимальном плане перевыполняется. Перевыполнение целесообразно по той продукции, производство которой способствует достижению максимума критерия оптимальности. Чем выше оценка, тем более дефицитен ресурс (продукция). 1 св-во относится к уровню стратегического планирования, используется менеджментом компании при планировании производственной программы на след. цикл, решает какие активы продавать / покупать и какие источники финансирования для этого использовать.

2. Оценка – мера влияния ограничения на функционал модели.

↑ (↓) недефицитного ресурса ↑ (↓) его остаток, производство продукции не изм-ся. Оценка ресурса –его пред.пол-ть. Так, при максимизации дохода дефицитность ресурсов определяется способностью приносить дополнительный доход. Влияние ограничений по выпуску на критерий оптимальности обратно влиянию ограничений по ресурсам. Если продукция невыгодна, то увеличение планового задания заставит повысить ее выпуск. это ведет к уменьшению выпуска выгодной и ухудшает план. При изменении плановых заданий по выпуску выгодной продукции ничего не меняется, т.к. ее выпуск в оптимальном плане выше заданий. При максимизации прибыли невыгодность продукции определяется ее способностью уменьшать прибыль. Пользуются практически все: Собственники капитала; Менеджмент среднего звена; На этапе финансового планирования производства; Кредиторы, банки, потенциальные инвесторы, клиенты.

3.Оценка – средство определения эффективности технологических способов производства.

По 2ТДб j-я продукция по s-ой технологии в оптимальном плане не производится, если потенциальный эффект превосходит реальный. Если потери от отвлечения ресурсов от других технологий превосходят результат, то данная технология невыгодна. Используется на этапе планирования производства нового продукта.

4.Оценка – средство балансировки затрат и результатов.

В 1ТД правая часть показывает общий размер совокупной «способности» ресурсов приносить доход, который снижается совокупной «способностью» задания по выпуску уменьшать доход. Производство продукции тратит эти «способности», что компенсируется получением реального дохода. План оптимален, если затраты полностью компенсируются результатами. Св-во используется для группы взаимозаменяемых ресурсов.

Вопрос 8. Производственная функция предприятия. Способы моделирования. Практическое значение в задачах анализа и прогнозирования рыночной деятельности предприятия.

Производственной функцией называется функция, выражающая количественную взаимосвязь производственных затрат и выпуска продукции. Нужна для изучения эфф-ти средств пр-ва и труда.

– вектор факторов производства (под факторами производства обычно понимают все факторы, влияющие на результаты производства, которые можно выразить количествен).

- j-й элемент производственного капитала (в стоимостном выражении),

- экономическая область фирмы, которую иначе называют областью производственных возможностей, включающей все допустимые наборы производственных факторов , которые могут быть приобретены предприятием с использованием оборотного капитала величиной M.

Определение. Экономическая область предприятия задается множеством векторов факторов производства в пространстве :

Определение. Производственной изоквантой уровня C для заданной технологии называется множество векторов , которым соответствует одна и та же стоимостная оценка результата

Определение. Частично упорядоченное множество , все двухэлементные подмножества которого имеют точную верхнюю грань, принадлежащую Ω, называется верхней полурешеткой и обозначается .

Рассмотрим среднесрочный интервал планирования, где - запас j-го ингредиента. Если в евклидовом пространстве J (размерность пространства производственной функции) мы рассматриваем положительные актанты (экономическая область фирмы), то в каждой конкретной точке экономической области определена структура производственного капитала . В каждой точке экономической области решается задача на максимум, т.е. из всех возможных выпусков выбирается наибольший в стоимостном выражении .

Факторы – ОК, ОбК, Труд. И в каждой точке, описываемой этой сеткой, получаем свое значение выпуска F(0,0,0) =0, F(макс,макс,макс)=Fmax

Определение. Функция , где - подмножество экономической области Ω, включающее наборы факторов производства, принадлежащих производственной изокванте , называется частичной производственной функцией. Определение. Функция , где верхняя полурешетка, включающая все допустимые изокванты I, называется полной производственной функцией. ППФ задается выражением

ЧПФ задана конкретно в узлах решетки, но отражает реальный процесс производства. Следующий этап планирования: на основе ЧПФ необходимо получить полный ее аналог, т.е. желательно, чтобы ППФ сохраняла основные характеристики ЧПФ и обладала бы определенными свойствами обычной аналитической зависимости: ППФ монотонно неубывающая; обладает свойством гладкости в смысле принадлежности к классу (где k – степень гладкости ф-и) непрерывно дифф-мых на ЭО функций. Чем выше k, тем меньше возможность построить ППФ, совп-ю с ЧПФ в узлах дискретной решетки.

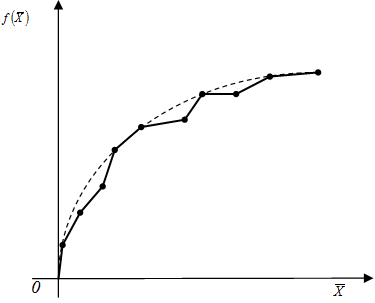
В качестве возможных отношений (мер отличия) ρ, как правило, используются следующие метрики:

1) равномерное приближение:

, ;

2) среднеквадр приближ (Евклидово расст):

Для целей практических исследований достаточно, чтобы ППФ f являлась дважды непрерывно дифференцируемой на экономической области.

Резюмируя изложенное, приведем основные этапы моделирования ППФ:

1. выбираем шаг и строим дискретную решетку;

2. В каждой точке экономической области фирмы Ω, соответствующей узлу дискретной решетки, решаем задачу определения наибольшего (в стоимостном выражении) объема выпуска, что позволяет в табличной форме построить ЧПФ;

3. Определяем принадлежность ППФ к определенному классу непрерывных аналитических зависимостей и выбираем метрику ρ, характеризующую близость ЧПФ и ППФ;

4. Оцениваем качество приближения (желательно определить те подобласти, где качество приближения является удовлетворительным). Возвращаемся к пункту 3, либо делаем вывод об удовлетворительности полученного образа ППФ f.

Если в виде изоквант: Вдоль изокванты приращение df=0

Оценим случай, когда меняются только 2 производственных фактора:

, -предельная замена произв.факторов обратно пропорциональна их двойств.оценкам.

Множество производственных изоквант образуют верхнюю полурешетку, которая имеет минимальный и максимальный элементы, изокванты не пересекаются.

Верхняя решетка:

• упорядоченное множество наборов ресурсов. На одном уровне находятся все такие наборы, наиболее эффективное исполнение которых дает один и тот же хозяйственный результат.

• добавление в каждый набор хотя бы 1 ед. ресурса либо оставляет нас на том же уровне (если ресурс не является дефицитным), либо переводит на новый уровень иерархии, соответствующий большей величине выпуска.

• верхняя полурешетка является дискретной или конечной. Число уровней конечно, что соответствует конечности множества производственных возможностей.

При переходе от ЧПФ к ППФ возможности моделирования существенно расширяются: между двумя любыми изоквантами можно поместить любое количество изоквант – это отличие непрерывной функции от дискретной.

Все ПФ имеют 4 характеристики:

1. коэффициент предельной эффективности факторов (показывает эффективность влияния фактора на результат) - на сколько единиц изменится результативный показатель при изменении фактора на единицу.

2. коэффициент эластичности показывает, насколько % изменится результативный показатель при изменении фактора на 1 %.

3. изокванта – линия равного результативного показателя (линия выпуска).

4. коэффициент взаимозамещения факторов: для двухфакторных -показывает, какое количество факторов X₁ требуется для замещения единицы X₂.

Исторически ПФ создавались для описания макроэкономических процессов (ф-ция Кобба-Дугласа). На микроуровне ПФ должна разрабатываться для каждого предприятия в отдельности. ПФ описывает процесс преобразования факторов производства в результат производства. ПФ помогает:

1. оценить эффективность использования совокупного производственного капитала, а также привлекаемых заемных средств;

2. оценить эффективность различных видов деятельности (производственная, финансовая, инвестиционная деятельность)

3. Получать прогнозные значения выпуска продукции, прибыли предприятия, а также значения макроэкономических показателей на основе информации о факторах производства и т.п.