Вопрос 7. Экономическое содержание двойственности. Способы получения и практическое использование оценок ресурсов и технологий.

Концепция двойственности в экономических задачах может быть сформулирована фразой: получить максимальный результат (в виде прибыли) с минимальными затратами. Т.е. одинаково важен и результат, и затраты. Особенно в сферах производства и потребления. Правильная постановка задачи: максимизировать количественный критерий при ограниченных затратах.

Простейшая модель оптимизации производства по критерию максимума дохода в случае, когда для производства j-й продукции используется один способ производства Т_j ( j = 1,2,..., n).

(2.7-2.9)

Состояние производственной системы задается вектором интенсивностей использования технологий Т₁,..., Т_n. Вектор “выпуск-затраты”, описывающий функционирование производственной системы, имеет вид . Выпуск товарной продукции = , а затраты i-го ресурса = .

Каждый ресурс обладает “теневой ценой”, определяющей ценность данного ресурса для предприятия с точки зрения дохода от реализации продукции и зависящей от наличного запаса и потребности в нем для выпуска. Если исп-ся только 1 ресурс и его надо много, то теневая цена этого ресурса будет велика. Этот произв. способ нерационален.

Эконом рез-т совп с затрач-и ресурсами, исчисл-ми в их теневых ценах. Оптимальные теневые цены называют объективно обусловленными оц (о.о.о.) или оптимальными оц, или двойственными.

Для определения о.о.о. ресурсов составим самостоятельную задачу ЛП.

у_i ( i =1,2,..., m) - о.о.о. i-го ресурса. Надо чтобы сумма теневых цен ресурсов, затрачиваемых при любом используемом производственном способе, не была меньше величины дохода р_j :

Таким образом, задача определения о.о.о. ресурсов формулируется как следующая оптимизационная задача:

Задача ЛП (2.21)-(2.23) называется двойственной задачей. Связь:

• прямая на максимум, двойственная — на минимум;

• коэффициенты целевой функции в прямой задаче являются свободными членами в ограничениях двойственной задачи и наоборот;

• коэффициенты при переменных в ограничениях двойственной задачи являются столбцами матрицы коэффициентов ограничений прямой задачи;

• знаки неравенств в системе ограничений прямой задачи меняются на противоположные в системе ограничений двойственной задачи.

У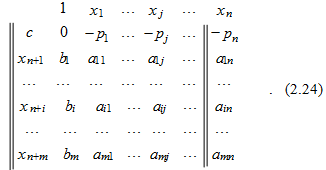 становим связь между решениями прямой и двойственной задач линейного программирования. Примем в прямой задаче переменные x₁,..., x_n за свободные и сформулируем ее в виде модели, обозначив переменные группы t_i через переменные x_{n+ i} :

с = 0 -  max;

x_{n+ i} = b_i - , x_{n+ i}   (i=1,2,..., m);

х_j  0 (j=1,2,..., n).

В двойственной задаче примем за свободные переменные у₁ ,..., у_m и сформулируем ее в следующем виде:

q = 0 +

у_{m+ j} = -

у _i  ; ( i =1,2,..., m).

у_{m+ j} — превышение теневой цены вектора затрат по i-му способу над доходами, выраженными в р _j.

Задачи описываются одной и той же матрицей, в которой должно быть установлено следующее соответствие между переменными:

(2.26)

Любое преобразование матрицы (2.24) по правилам симплекса приводит к новой матрице, которая описывает новое допустимое (или опт) решение.

Теоремы Дв-ти:

1)равенство экстремальных значений целевых функций (верхний левый угол таблиц коэффициентов в последней симплекс-таблице). Те в оптимальном состоянии суммарный выпуск предприятия совпадает с затратами производственных ресурсов, исчисленными в их теневых ценах.

2) свободные переменные в оптимальном решении прямой задачи (принимают нулевое значение) соответствуют базисным переменным оптимального решения двойственной задачи (принимают положительные значения) и наоборот. Таким образом, справедливы следующие соотношения “дополняющей нежесткости”:

(2.28)

Если i-й производственный ресурс является недефицитным (выражение в скобках положительно), то его теневая цена равна нулю т.е. y=0. Если j-й производственный способ является интенсивным, т.е. , то величина выпуска р _j совпадает с затратами производственных ресурсов по этой технологии (т.е скобка=0).

Свойства двойственных оценок: