Вопрос 29. Робастное статистическое оценивание

При статистическом исследовании часто встречаются данные, которые по своим значениям сильно отклоняются от основного массива. Они называются выбросами, засорением или грубыми ошибками.

Пример

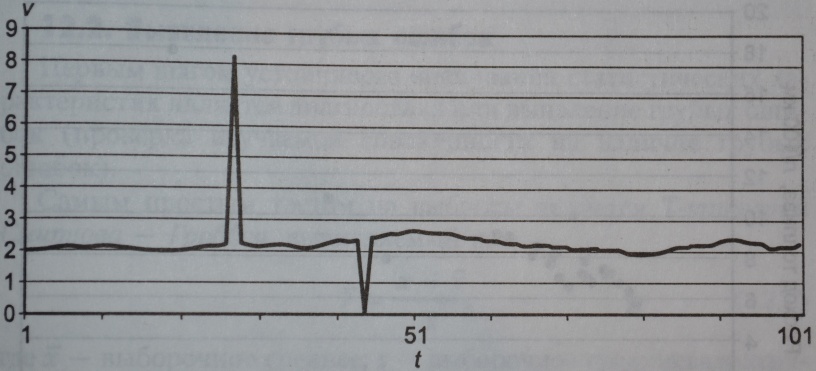
Искажают структуру статистической совокупности и вносят смещения в интегральные параметры.

Основные причины выбросов:

1. Особенность распределения, например нормальное распределение с минимальное вероятностью допускает сколь угодно больших значений (т.е. величина на самом деле не является ошибкой).

2. Неправильное причисление данных к исследуемой совокупности (ошибки группировки, типологической классификации).

3. Ошибка при регистрации и обработке исходной информации (ошибка оператора).

Решением проблем нахождения, устранения выбросов и получения адекватных оценок статистических показателей занимается специальный раздел статистики – робастное (устойчивое) оценивание. Первый шаг робастного оценивания – это выявление грубых ошибок.

Методы выявления ошибок:

1. Т-критерий Смирнова-Граббса (для нормально распределенных случайных величин).

Для нетипичного значения рассчитывают:

; – выборочное среднее

– выборочное среднеквадратичное отклонение; – нетипичное значение

Сравнивается с критическим значением метода Смирнова-Граббса на уровне значимости .

- наблюдение не нарушает однородности выборки;

- наблюдение грубо нарушает однородность выборки и является нетипичным;

- требуются дополнительные аргументы для классификации наблюдения.

2. Дисперсионный критерий Граббса (сравнивает исходную и усеченную дисперсии). Проверяет на аномальность отдельное значение.

Совокупность выстраивается в вариационный ряд . Грубые ошибки концентрируются на хвостах ряда. Для проверки аномальности минимума вычисляются:

• выборочное среднее

• усеченное выборочное среднее

• статистика критерия Граббса

Для проверки аномальности максимального то же самое, но отрезаем с конца:

• ; ;

Значение статистик и варьируются в интервале от 0 до 1. Чем ближе значение к 1, тем меньше отличие между усеченной и исходной выборками.

Полученное значение сравнивается с критическим значением на уровне значимости . В исходах сравнения выделяют следующие случаи:

- наблюдение не нарушает однородности выборки;

- наблюдение грубо нарушает однородность выборки и является нетипичным;

- требуются дополнительные аргументы для классификации наблюдения.

В случае, когда в совокупности несколько выбросов и их значения плотно группируются, критерий Граббса не работает.

3. L-критерий Титьена-Мура. Предназначен для выявления групп из k>1 выбросов.

Показатели для минимумов:

• выборочное среднее ; усеченное выборочное среднее

• статистика критерия

Для максимумов:

• выборочное среднее ; усеченное выборочное среднее

• статистика критерия Граббса

Полученные значения сравниваются с критическими значениями аналогично критерию Граббса.

4. Обобщенный E-критерий Титьена-Мура. Применяется при предположении, что выбросы распределены симметрично в нижней и верхней частях вариационного ряда . Алгоритм:

• расчет среднего для всей выборки

• расчет модулей отклонений

• ряд упорядочиваем по значению . Полученный ряд обозначим , ,

• расчет среднего усеченного по k нетипичным значениям

• расчет статистики критерия

Полученное значение сравнивается с критическим значением аналогично критерию Граббса.

Устойчивое оценивание

Если предварительный анализ указывает на наличие грубых ошибок в выборке, то далее возможны два подхода: исключить объекты с грубыми ошибками или модифицировать их.

В многомерном случае устранение объекта из исследуемой совокупности зачастую неприемлемо. При этом может возникнуть необходимость определить устойчивые усеченные интегральные характеристики (мат. ожидания и т.д.). Для этого используют следующие методы:

1. Метод Пуанкаре расчета устойчивого среднего (режет распределение с двух сторон, т.к. 2k). Это пример наиболее простого варианта устойчивого оценивания статистических характеристик, путем оценки по усеченной совокупности данных, в которой устранены грубые выбросы.

,

где k - число грубых ошибок, равное целой части от (т.е. k=[ ;

n - объем совокупности;

- специальный параметр, зависящий от теоретической частоты e ошибочных данных. Например, если по предыдущему опыту известно, что 1% данных ненадежны, то е принимается равным 1%. Значение при выбранном уровне е можно определить по таблице.

2. Метод Винзора модификации данных. Получаем не усеченное, а новое математическое ожидание. Применяется к симметричным распределениям. По сути метод Винзора в одномерном случае заключается в замене первых k значений вариационного ряд на , последних – на .

Устойчивое среднее значение по Винзору определяется по следующей формуле:

где k вычисляется таким же образом как в методе Пуанкаре.

В случае многомерного засорения данных, когда выбросами являются не отдельные значения признаков, а векторы, можно использовать критерий Хоттелинга для проверки значения вектора x:

где n – количество объектов; m – количество признаков; x – нетипичный вектор;

S – ковариационно-дисперсионная матрица. , где F – квантиль F-распределения

Если Т>T_табл, то вектор признается аномальным.

Вопрос 30. 1.Основные поняия системного анализа.2. Свойства систем. 3.Особенности сложных систем. 4.Классификация методов моделирования. 5.Иерархия моделей. 6.Методы формализованного представления систем.

1.Основные системные понятия

Система – это совокупность элементов, объединённых общей функциональной средой и целью функционирования. Система не сводима к сумме своих элементов, элементы выступают и воспринимаются, как единое целое. Элементы вне системы другие. Связь элементов внутри системы сильнее, чем связь с элементами других систем.

К основным особенностям систем можно отнести:

• Система обладает новыми свойствами по сравнению с элементами

• Системы обладают свойствами оптим-ти, то есть проектируется по критериям оптим-ти

• Система создаётся для достижения какой-то цели

Цель – это вариант удовлетворения исходной потребности, выбранной из некоторого множества альтернатив, сформулированная на основе специального знания. Потребность – это категория объективная, а цель – субъективная, определяющаяся имеющимся опытом.

Цели реальных систем могут быть следующими:

1. Требуемое конечное состояние системы

2. Требуемый порядок смены состояния

3. Требуемое направление движения системы без фиксации конкретной конечной точки

Элемент системы – это условно неделимая самостоятельно функционирующая часть системы.

Компонент системы – это множество относительно однородных элементов, объединённых общими функциями при обеспечении выполнения общих целей развития системы.

Подсистема –комп-т, кот. сам рассматривается как сложная система.

Структура системы – это совокупность связей.

Эмерджентность (целостность) – это такое свойство системы S, которое принципиально не сводится к сумме свойств элементов, составляющих систему, и не выводится из них.

Свойство системы не является простой суммой свойств, составляющих её элементы (части). Свойства зависят от свойств элементов. Элементы утрачивают часть своих индивид.свойств но могут приобрести новые. Система иерархична, есть обратные связи, имеет предельное состояние.

ОТКРЫТЫЕ и ЗАКРЫТЫЕ системы

Большая система - невозможно исследовать иначе, как по подсистемам.

Сложная - строится для решения многоцелевой и многоаспектной задачи. Ее признаки:

Неопределённость и большое число элементов, Эмерджентность, Иерархия , Агрегатирование – объединение нескольких параметров системы в параметры более высокого уровня, Многофункциональность , Гибкость – способность системы изменять цель функционирования, Адаптация , Надежность , Безопасность , Стойкость , Уязвимость , Живучесть – способность изменять цели функционирования при отказе или повреждении элементов системы.

Сложные характеризуются большим числом элементов и связей между ними.

свойства сложных систем:

• Скачкообразное изменение поведения при переходе из одного состояния в другое

• Можно оц.интегр.показатели системообразующих свойств, этого достаточно

• Изменение состояния системы происходит закономерно.

3. Особенности сложных систем- можно сравнить с движением неупругого шарика, скатывающегося по лестнице с очень широкими и низкими ступеньками:

• В состоянии покоя шарик может находиться только на одной ступени.

• Если движение происходит, шарик, как бы быстро он не катился, движется в пределах ступени гораздо более длительное время, чем перескакивает со ступени на ступень.

• С одной ступени шарик может перекатиться только на соседнюю. Это означает, что из одного фиксированного состояния система не может перескочить в любое произвольное состояние, а только в одно из близких соседних предсказуемых состояний.