Вопрос 27: основные понятия теории линейного программирования. Теоретические основы симплекс-метода.

Задача ЛП – однокритериальная задача условной (с ограничениями) оптимизации с линейным функционалом и линеными ограничениями. Пример - задачи о фанерном цехе, о составлении рациона, классическая транспортная задача, динамическая задача планирования производства.

Три формы записи задач:

Станд	Канонич	Общ
(c,x)=>max(x) Ax<=b x>=0	(c,x)=>max(x) Ax=b x>=0	(c,x)=>max(x) Aixi<=bi; Ajxj=bj x>=0

Графический метод решения задач.

Тут нужен любой пример. В лекциях была такая задача:

«Полезные выводы», которые надо сделать на основе графического решения:

1. решение задачи ЛП находится на границе допустимого множества;

2. множеством решений может быть: ø, точка, отрезок, луч, прямая.

3. Если решение достигается, то это присходит в одной крайних точек.

4. В силу конечности крайних точек, задача сводится к их перебору.

5. Хотелось бы от общего перебора перейти к направленному, например, с постоянным улучшением функционала.

Можно предложить геометрические наброски для организации подобного: рассматривать углы между и ребрами. Если нет острого, то крайняя точка – решение.

Во всех случаях задача ЛП сводится к канон по форме записи:

.

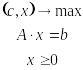Все взаимосвязи носят линейный характер. m – количество огр-й, n – количество перем-х, n > m.

, x_b – базисные, x_s – свободные.

A_b = (a₁….a_m)– базисные столбцы. A_s = (a_m+1….a_n)– свободные столбцы.

, ,

Если x_s = 0, – базисное решение. Базисное решение может оказаться недопустимым.

Т. Если множество допус-х значений задачи ЛП не пусто, то в нем  хотя бы одно базисное решение.

Т. Множество допустимых базисных решений задачи ЛП совпадает с множеством крайних точек допустимого множества решений этой задачи.

Т. Если задача ЛП имеет решение, то оно достигается хотя бы в одной из крайних точек.

Симплекс метод.

Предполагается, что есть допустимое базисное решение – x_b x_s (базисные и свободные компоненты).

A_bx_b+A_sx_s=b => b. Функционал тоже можно разделить на c_b и c_s.

=cx⁰ + dx_s

_{Dj=(cs - cb Ab-1 As )} – симплекс разности. f(x)=f(x0) + ∑djxj, т.е..насколько можно увел.ф-л, увеличив своб.перем.

Важные выводы:

1. если все симплекс разности  0, то значение целевой функции улучшить нельзя, то есть перед нами опт.решение задачи;

2. не базисный столбец a_j имеет смысл вводить в базис, если симплекс разность > 0;

3. можно выбирать наибольшую из положительных симплекс разностей d_j.

Пусть a_r – столбец, который было решено ввести в базис.

 остальные из свободных переменных останутся свободными.

.

 l

l – это одна из базисных переменных, индекс той переменной, которая реально выводится из базиса.

Значение x_l = 0 для этого нового базиса. Сам симплекс метод сводится к следующему:

1. Имеем базисное решение. Для него формируем A_b, A_s, C_b, C_s, X_b, X_s.

2. Вычисляем сиплекс разности. Если все они  0, получено решение, конец процедуры. Если нет, вводим в базис столбец a_r.

3. Если , то функционал можно увести в +, а если нет – .

4. Вычисление нового базисного решения

5. Переход к 1.