Вопрос 26. Формулировка задачи Больца. Принцип максимума как распространение метода множителей Лагранжа на решение задачи Больца.

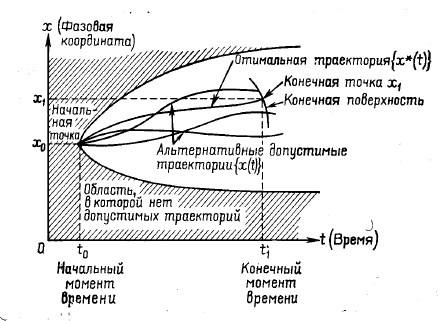
Задача управления в классическом вариацион­ном исчислении состоит в следующем: среди множества функций времени — фазовых траекторий,— соединяющих две фиксированные точки, соответствующие начальному и конечному моментам времени, требуется выбрать функ­цию, максимизирующую некоторый интеграл от заданной функции, которая зависит от фазовой координаты, скоро­сти изменения фазовой координаты и времени.

При строгой формулировке задачи управления используются следующие понятия: время (момент времени), фазовые координаты, управляющие параметры, уравнения движения, определение конечного момента, целевой функционал.

= (x, u, t)dt + F (x₁, t₁)

= f (x, u, t) – скорость изменения каждой фазовой корд-ты (это ур-я движения)

x (t₀) = x₀, x (t₁) = x₁, {u (t)} .

T-время; x(t) – вектор фазовых координат; u(t) –вектор управляющих.параметров; U- допустимое мн-во упр.парам-ров. x (t₀) = x₀, x (t₁) = x₁, - нач.и кон.состояния системы. I (…), F (..) и f (…) – заданные непрерывно дифференцируемые функции; t₀, x₀ – фиксированные параметры; t₁ или x₁ – фиксированные параметры (либо с помощью уравнения T (x, t) = 0 определяется конечная поверхность).

фазовая траектория {x (t)} = {x (t) }

Управление («траектория управления») {u (t)} = {u (t) }.

Управлением («траекторией управления») называется функция

{u (t)} = {u (t) }. (11.1.7)

U(t)- кусочно-непрерывная функция времени. u (t) .

Ω - выпуклое и компактное, инвариантное относительно времени.

При решении задач методом Лагранжа вводят множители Лагранжа для каждого ограничения, затем строят Лагранжиан и ищется максимум по исходным переменным и минимум по новым переменным. Принцип максимума - распространение метода множителей Лагранжа на задачи динамической оптимизации (задачи управления).

при решении задачи с помощью принципа максимума сначала вводятся n сопряженных переменных y (t) и определяется ф-я Гамильтона H (x, u, y, t) = I (x, u, t) + yf (x, y, t).

Затем отыскиваются функции {u (t)}, {у (t)} и {x (t)}, удовлетворяющие следующим условиям:

(x, u, y, t) при всех t, ,

, x (t₀) = x₀ (14.1.29)

, .

Эти условия необходимы для существования локального максимума. Форма искомого решения, т.е. оптимального управления, очень часто может быть найдена непосредственно в результате максимизации гамильтониана.

ДАЛЕЕ ДОКАЗАТЕЛЬНАЯ ЧУШЬ, КОТОРАЯ НЕВНЯТНАЯ И ВРЯД ЛИ НУЖНАЯ

Пример: фиксирован конечный момент времени, а на управляющие параметры не накладываются никакие ограничения. Это задача максимизации при наличии ограничений. Максимизируемое выражение представляет собой целевой функционал

J = (x, u, t)dt + F (x₁, t₁), (1)

Огр-я: f (x, u, t) – (t) = 0, . (2)

Введем вектор-строку новых переменных – по одной переменной для каждого из n ограничений

y (t) = . (3)

Эти сопряженные переменные - динамические эквиваленты множителей Лагранжа. Определим функцию Лагранжа = ф-л плюс скалярное произведение вектора множителей Лагранжа и вектора ограничений. Поскольку ограничения и y(t) определены на всем временном промежутке, то произведение следует определить с помощью знака интеграла.

L = J + [f (x, u, t) – ]dt = {I (x, u, t) + y[f (x, u, t) – ]} + F (x₁, t₁). (4)

Седловая точка лагранжиана определяет решение. Точка ({u*(t)}, {y*(t)}) представляет собой седловую точку, если L ({u(t)}, {y*(t)}) L ({u*(t)}, {y*(t)}) L ({u*(t)}, {y(t)}). (5)

Тогда траектория управления {u*(t)} является решением задачи управления.

Необходимые условия существования седловой точки. Из (4) следует, что переход от сопряженных переменных у (t) к {y (t) + Δy (t)}, где Δy (t) – произвольная непрерывная функция времени, изменит функцию Лагранжа на

ΔL = y[f (x, u, t) – ]dt. (10)

Так как необходимое условие первого порядка для существования минимума L относительно {у (t)} требует, чтобы ΔL = 0, то, согласно основной лемме вариационного исчисления, должны выполняться уравнения движения, т.е.

= f (x, u, t). (11)

Выведем теперь остальные необходимые условия.

Если в (14.1.4) проинтегрировать по частям выражение у (t) (t), то L преобразуется к виду

L = (x, y, t) + yf (x, u, t) + х}dt + F (x₁, t₁) – [у (t₁) x (t₁) – у (t₀) x (t₀)]. (12)

Первые два слагаемых, стоящих под знаком интеграла, являются по определению функцией Гамильтона:

H (x, u, y, t) = I (x, u, t) + yf (x, y, t). (13)

L = (x, u, y, t) + х}dt + F (x₁, t₁) – [у (t₁) x (t₁) – у (t₀) x (t₀)]. (14)

Исследуем результат перехода от ТУ {u (t)} к {u (t) + Δu (t)} и соответствующего перехода с фазовой траектории {x (t)} на фазовую траекторию {x (t) + Δx (t)}. При этом

ΔL = , (15)

где

, . (16)

Так как для существования максимума необходимо, чтобы приращение лагранжиана ΔL обращалось в ноль, и поскольку (15) должно выполняться при любых {Δu (t)}, то

, , (17); , , (18); , (19)

Необходимые условия (17) показывают, что в каждой точке оптимальной траектории функция Гамильтона достигает максимума относительно управляющих параметров. При этом r условий (17) являются условиями существования внутреннего максимума, так как в рассматриваемой задаче не наложено никаких ограничений на значения управляющих параметров. В общем случае, если на значения управляющих параметров наложены некоторые ограничения, условия (17) принимают вид

(x, u, y, t) при всех t, , (14.1.20)

т.е. в точках оптимальной траектории в каждый момент времени функция Гамильтона достигает максимума относительно управляющих параметров. Следовательно, в любой момент времени t из указанного промежутка достигается либо внутренний максимум, при котором, как и в классических задачах математического программирования,

, (21)

либо максимум достигается на границе. В последнем случае, как в нелинейном программировании,

, (14.1.22)

где n – вектор нормали к границе области Ω.

Необходимые условия (14.1.18) и (14.1.19) представляют собой соответственно ДУ и граничные условия для сопряженных переменных. ДУ показывают, что скорость изменения каждой из сопряженных переменных равняется частной производной функции Гамильтона по соответствующей фазовой координате, взятой со знаком минус. Граничные условия показывают, что конечное значение каждой из сопряженных переменных равно частной производной функции F (x, t) по соответствующей фазовой координате.

Используя функцию Гамильтона, можно представить дифференциальные уравнения для фазовых координат, т.е. уравнения движения, в виде

. (23)

Данные дифференциальные уравнения для фазовых координат и дифференциальные уравнения для сопряженных переменных плюс все граничные условия образуют систему уравнений, называемых каноническими уравнениями

, x (t₀) = x₀

, . (14.1.24)

Эта система состоит из 2n дифференциальных уравнений, на одну половину которых наложены граничные условия, заданные в начальный момент, а для оставшихся n уравнений граничные условия заданы в конечный момент.

Рассмотрим теперь, как функция Гамильтона изменяется во времени. Так как H = H (x, u, y, t), то

. (14.1.25)

Преобразуем это выражение, используя уравнения движения

. (14.1.26)

Первый член этого выражения равен нулю в точках оптимальной траектории, в силу дифференциального уравнения для сопряженных переменных. Второй член обращается в нуль потому, что либо частная производная равна нулю, если максимум внутренний, либо обращается в нуль, если максимум достигается на границе. Следовательно, в точках оптимальной траектории

. (14.1.27)

В частности, если задача является автономной, т.е. если I (…) и f (…) не зависят явно от времени, то и гамильтониан не зависит явно от времени и, следовательно, функция Гамильтона постоянна во времени в точках оптимальных траекторий, так как dH/dt = 0.

Итак, при решении задачи с помощью принципа максимума сначала вводятся n сопряженных переменных y (t) и определяется функция Гамильтона

H (x, u, y, t) = I (x, u, t) + yf (x, y, t). (14.1.28)

Затем отыскиваются функции {u (t)}, {у (t)} и {x (t)}, удовлетворяющие следующим условиям:

(x, u, y, t) при всех t, ,

, x (t₀) = x₀ (14.1.29)

, .

Эти условия необходимы для существования локального максимума. Форма искомого решения, т.е. оптимального управления, очень часто может быть найдена непосредственно в результате максимизации гамильтониана. При этом оптимальные управляющие параметры обычно определяются не как функции времени, а как функции сопряженных переменных. Для того чтобы записать управляющие параметры в виде функций времени, требуется предварительно определить, как зависят от времени сопряженные переменные. Это в свою очередь приводит к необходимости решать двухточечную граничную задачу, представленную каноническими уравнениями с граничными условиями. В этой системе, состоящей из 2n дифференциальных уравнений, для n уравнений заданы конечные граничные условия (относительно сопряженных переменных).