Вопрос 24. Методы стохастической многокритериальной оптимизации

Нужно для управления сложными системами. Особенность именно стохастической оптимизации – все переменные не детерминированные, а случайные (спрос, курсы валют, курсы акций). Детерминированные – запланированные затраты, инвестиции. Разница в том, что здесь мы максимизируем или минимизируем матожидания, квантили, отклонения – смотря что нас интересует. Соотвественно переменные тоже в виде матожиданий и тд представлены. В остальном методы такие же, как для детерминиированных процессов (в последнем вопросе):

Постановка задачи: Пусть имеются критерии . Требуется найти точку , которая оптимизирует все эти критерии. Критерии называют частными критериями. В совокупности они образуют векторный критерий . А именно, рассматривается задача: при условии .

Обычно нет решения, минимизирующего все частные. => нужно искать компромиссное решение. Их стараются найти в классе так называемых эффективных решений (множество Парето).

Метод аналитической иерархии. Общая схема МАИ. Постановка задачи:

1.Задана общая цель (n), назначена соответствующая система, которая должна оптимизироваться.

2. Задано произвольное число альтернатив, из которых нужно выбрать лучшее

3. Задано произвольное число частных критериев, по которым анализируются эти альтернативы.

Требуется найти наилучшую альтернативу. Атрибуты:

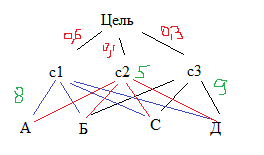1. Н а первом шаге задача оптимизации структурируется в виде соответствующей иерархии ( цели, критерии и альтернативы).

Сумма показателей равна 1.

Va=8*0,6+5*0,1+9*0,3=8

2. Реализация попарных сравнений для элементов каждого уровня с учетом специфики требований элементов более высокого уровня иерархии. При этом результаты попарных сравнений реализуются в виде матрицы, по которым затем определяется веса важности этих элементов

3. Определяются количественные индикаторы альтернативы, называемые приоритетами.

Шкала сравнений: 1.Эквивалентны (1) 2.Умеренное превосходство (3-1) 3.Существенное превосходство (5-1) 4.….(7-1) 5.….(9-1)

Матрица сравнений сравнивает каждый элемент с каждым:

	А	Б	С	Д	сумма	Нормируем	Итог
А	1	2	3	6	12	1/2	1*1/2+2*1/4+3*1/6+6*1/12=2
Б	1/2	1	3/2	3	12/2	1/4	1
С	1/3	2/3	1	2	12/3	1/6	4/6
Д	1/6	1/3	1/2	1	12/6	1/12	4/12
сумма					24	1

Свойства матрицы:

• a_ii=1, для любых i

• aij=1/aji =>aij*1/aji=1 – обратно симметричная матрица

• aik*akj=aij

• vi/vk*vk/vj=vi/vj – согласованная матрица

1. Перед нами несколько функций: одну нужно максимизировать, другую минимизировать и т.п.

Множество Парето – общее у всех. Как его найти?

1. g⁽¹⁾(x)->max => 1/ g⁽¹⁾(x)->min (все задачи необходимо сводить на мин.)

2. g⁽²⁾(x)->min

3. …

Нужно найти наилучшее решение х1…хn, которое минимизирует все эти функции.

Частный случай: Абсолютное решение. Ситуация, когда все функции можно минимизировать. Решение наз-ся абсолютным, когда оно оптимизирует одновременно все частные критерии.

Решение называется Парето оптимальным, если нельзя улучшить показатель хотя бы одного критерия, при этом чтобы не ухудшились показатели другого критерия. Необходимо использовать прямые методы: задача должна сводиться к однокритериальной.

Опр. Решение называется эффективным или оптимальным по Парето, если нет другого решения такого, что , причем хотя бы для одного “<”.

Бывает несколько парето-опт. Тогда необходим доп. перебор эфф. решений. Приёмы:

• методы сведения задач многокритериальной оптимизации к задачам скалярной оптимизации;

• методы компенсации;

• методы порогов сравнимости.

Оптимизация основного частного критерия

Среди частных критериев выделяется один, принимается как основной. Для остальных указываются приемлемые значения.

Метод взвешенной суммы оценок частных критериев

Формулируется скалярный критерий как взвешенная сумма оценок частных критериев:

— вес k-го критерия, задаваемый экспертами или непосредственно ЛПР с учетом особенностей исходной рассматриваемой задачи.

Минимаксный обобщённый критерий

На основе частных критериев исходной многокритериальной задачи формируется обобщенный критерий следующим образом: где — коэффициент важности каждого критерия (достаточно часто на практике в качестве коэффициента выбирают значение (gk это приемлемое значение критерия)). Точки минимума этой критериальной функции - искомое оптимальное решение.

Минимизация обобщённого скалярного критерия

Формируется скалярный обобщенный критерий

где — минимальное значение каждого частного критерия на допустимой области X.

Метод последовательных уступок

В случае, когда частные критерии могут быть упорядочены в порядке убывающей важности. Пусть — наиболее важный, — наименее.

1) решается однокритериальная задача для наиболее важного критерия:

Пусть — минимальное значение, полученное на первом этапе. Назначается некоторая уступка ∆₁ (∆₁ > 0), которую можно допустить в рамках реализации этого метода с учетом особенностей критерия по отношению к найденному значению , чтобы перейти ко второму этапу. На критерий налагается требование, согласно которому его оценка не должна превышать допустимой величины .

2) ищем решение, минимизирующее g⁽²⁾(x) при указанном ограничении на при указанном ограничении на и с учетом заданного множества X допустимых решений, т.е. решаем следующую однокритериальную задачу:

при ограничениях

И ТД.

Метод может приводить к решениям, не принадлежащим переговорному множеству решений, оптимальных по Парето. Другими словами, найденное решение может не быть эффективным.

Метод идеальной точки

Состоит в нахождении точки, дающей решение, ближайшее к так называемой утопической точке, которую, обычно, задает ЛПР, в виде желаемых значений показателей всех частных критериев. Найденную точку с указанным свойством и принимают в качестве наилучшего решения по методу идеальной точки. Пусть

Пусть — наилучшие значения этих критериев в .

Тогда в пространстве точку с координатами называют утопической точкой — УТ. Ближайшую (по метрике) к УТ точку, которую можно реализовать при заданных ограничениях , называют идеальной точкой. Метод идеальной точки может приводить к решениям, не принадлежащим границе Парето.

Методы компенсации

Используют идею возможного компромисса между противоречивыми оценками по паре (или по группам) критериев исходной задачи. Для каждой анализируемой альтернативы на одной чаше весов отмечаются достоинства оценок (по некоторой группе критериев), а на другой — недостатки (по другой группе критериев). ЛПР составляет два отдельных списка из достоинств и недостатков альтернативы. Затем после тщательного анализа определяет, какой недостаток (или их совокупность) можно считать эквивалентным определенному достоинству (или их совокупности). После чего такие «компромиссные» достоинства и недостатки вычеркиваются из списков.

Методы порогов сравнимости

К таким задачам относят серию методов ЭЛЕКТРА (ELECTRE). Идея такой группы методов состоит в использовании бинарных отношений между анализируемыми вариантами решений или альтернатив. Бинарные отношения соответственно определяют условия, при которых: 1) один вариант решения превосходит другой; 2) оба варианта решений эквивалентны; 3) оба варианта решений несравнимы между собой. При изменении условий меняется и количество сравниваемых альтернатив. При этом изменяется и состав так называемого ядра, состоящего из альтернатив, оказавшихся не худшими при всех сравнениях.

Компьютерные алгоритмы решающие такие задачи: (FMAA – Fuzzy Multicriteria Acceptability Analysis, ProMAA – Probabilistic Multicriteria Acceptability Analysis) базируются на вычислении

индексов приемлемости рангов альтернатив. Реализация методов FMAA и ProMAA основана на использовании численных методов для оценки функций от нечетких/случайных величин без применения методов Монте-Карло. Есть система поддержки принятия решений DECERNS WebSDSS, реализующая методы FMAA и ProMAA