Вопрос №16. Эконометрические модели с нестандартными ошибками

У нестандартных ошибок Cov()_²Е, что является следствием существования корр-и между ее разновременными значениями, и/или _²const (гетероскедастичность) или ошибка  может быть связана с х_i. Из-за этого оценки методов МНК и ММП теряют некоторые свои “качества” (эфф-ть). Исп-ся Обобщенный МНК (ОМНК) и ММП (ОММП), инструментальные переменные.

Математическое обоснование ОМНК базируется на свойстве положительно определенной^* ковариационной матрицы ,: =, (3.8) где матрица  — невырожд. ^–1()^–1=Е, (3.9) и ()^–1^–1=^–1. Предположим, что матрица  известна.

Домн слева на ^–1 и получим у*=Х*a+*, (3.11) где у^*=^–1у; Х_*=^–1Х ; _*=^–1 . (3.12)

Ков.матр вектора _* равна Е: Cov(_*)=M[_*, _*]=M[^–1_,^–1]=^–1^–1=E. (3.13) => _²=1.

Применяя к модели (3.11) обычный МНК, получим a=(Х_*Х_*)^–1Х_*у_*=(Х^–1Х)^–1Х^–1у. (3.14) Оценки несмещ и эфф.

В обобщенном ММП предполагается, что ()N(0,_). В этом случае плотность нормального закона распределения значений ошибки _t, t=1,2,... Т; можно представить в следующем виде: ()=  _ _y^–1].)= (₁ ₂... _T) _ _^–1],(3.18). При этом ₁ =₂=...=_Т.

При независимых ошибках ₁, ₂,..., _{Т ,}  ( )=

l= – ln(2) – ln_² – ln_– (у –Х)_^–1(у –Х). (3.19)

a=(Х_^–1Х)^–1Х_^–1у; _²= (у –Хa) _^–1(у –Хa). (3.21). Тк _=²_ , первое выражение можно записать в следующем виде: a=(Х_^–1Х)^–1Х_^–1у. (3.22)

Оценки ОММП обладают асимптотической несмещенности, состоятельности и эффективности.

Метод инструментальных переменных

Для получения несмещ-х (по крайней мере сост-х) оценок, когда есть корр-я между x_it и _t.

Пусть есть “инструм-е” переменные z_i, число к-х в общем случае совпадает с числом незав факторов х_i, i=1,2,..., n; и при t=1,2,..., Т, каждая из которых характеризуется нулевыми корреляционными вз/св с ошибкой модели . При заданном Т матрица значений Z имеет такой же размер, как матрица Х.

Умножим слева уравнение у=Х+ на матрицу Z. Получим Zу=ZХ+Z, (3.53). Тк M[Z]=0, умножая выражение (3.53) слева на (ZХ)^–1, непосредственно имеем a_z =(ZХ)^–1Zу, (3.54) где a_z – вектор оценок параметров эконометрической модели, полученный с использованием инструментальных переменных.(состоятельные)

Вопрос 17. Аналитическое решение и графическое решение игры 2*2. Возможности и перспективы применения теории игр при решении социально-экономических задач.

Седловая точка – пара чистых стратегий  (iо,jо) , при которых достигается равенство   наибольший элемент столбца матрицы игры, = наименьший элемент соответствующей строки. Т.е. если один из игроков придерживается стратегии, соответствующей седловой точке, то другой игрок не сможет поступить лучше, чем придерживаться стратегии, соответствующей седловой точке.

Аналитическое решение игры 2x2.

Условие СТ: max(минимумы по строкам) = min(максимум по столбцам)

Для игры, где нет СТ, в соотв. с осн. Теор. теории игр оптимальное решение есть и это пара смешанных стратегий (x*_{l ,}x*₂) и (у*₁,у*₂).

Чтобы найти, воспользуемся теоремой об активных стратегиях. Для игры 2x2 любая чистая стратегия противника является активной, если отсутствует седловая точка. Если первый игрок придерживается своей оптимальной смешанной стратегии, то его средний выигрыш будет равен цене игры v, какой бы активной стратегией ни пользовался второй игрок. (то есть выбираем такую пару (x*_{l ,}x*₂) , чтобы нам было все равно, как поступит 2й игрок, тогда риска нет). Пусть игра задана платежной матрицей

Средний выигрыш первого игрока, если он использует оптималь­ную смешанную стратегию х* = (х*_{1 ,} х*₂), а второй игрок— чистую стра­тегию 1, равен це­не игры v: . Если 2й игрок применяет стратегию 2, то . Приравниваем это и получаем сис­тему уравнений для определения оптимальной стратегии первого игрока и цены игры:

Решая эту систему, получим оптимальную стратегию и цену:

, ,

Так же для 2го игрока.

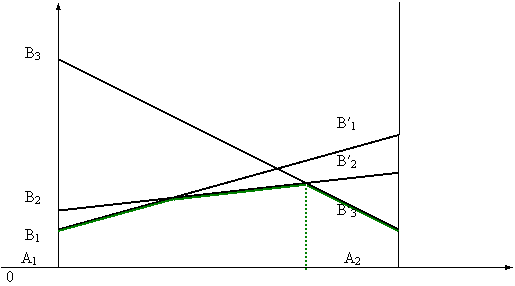
Графический метод. Этот метод применим только к играм, в которых хотя бы один игрок имеет только две стратегии (иначе просто не нарисуешь на плоскости). Рассмотрим игру 2*n. Пусть 1ый игрок выбрал смешанную стратегию Р=(р,1-р), а второй игрок – k-ую чистую стратегию. Ожидаемый выигрыш первого игрока линейно зависит от р: . На плоскости это уравнение описывает прямую. Поэтому на плоскости сначала рисуются все прямые w=a_1kp+a_2k(1-p) k=1…n. Затем для каждого значения р, 0p1 путём сравнения соответствующих ему значений w на каждой прямой определяется и отмечается наименьшее из них. В результате получается ломаная, которая и является графиком функции . Эта ломаная огибает снизу всё семейство прямых. Верхняя точка ломаной определяет и цену игры, и оптимальную стратегию первого. Аналогично находится решение для mx2 игр, только ломаная теперь огибает прямые сверху и нам нужна нижняя её точка.