Основні властивості невизначеного інтеграла

1. Похідна від невизначеного інтеграла дорівнює підінтегральній функції:

2. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу:

3. Невизначений інтеграл від диференціала деякої функції дорівнює цій функції плюс довільна стала:

4. Сталий множник можна виносити за знак інтеграла:

5. Невизначений інтеграл від алгебраїчної суми двох неперервних функцій дорівнює алгебраїчній сумі інтегралів від цих функцій:

№№№№№

Диференціальним рівнянням називається рівняння, у яке входять: незалежна змінна , шукана функція та її похідні або диференціали.

Символічно диференціальні рівняння записують так:

.

Диференціальне рівняння називається звичайним, якщо шукана функція залежить від одного незалежного змінного.

Порядком диференціального рівняння називається порядок старшої похідної або диференціала, що входить у дане рівняння.

Розв’язком або інтегралом диференціального рівняння називається така функція, яка перетворює це рівняння в тотожність.

Загальним розв’язком або загальним інтегралом диференціального рівняння називається такий розв’язок, до якого входить стільки незалежних довільних сталих, який порядок рівняння. Так, загальний розв’язок диференціального рівняння першого порядку має одну довільну сталу.

Частинним розв’язком диференціального рівняння називається розв’язок, знайдений із загального при різних числових значеннях довільних сталих.

Значення довільних сталих знаходять при певних початкових значеннях аргументу і функції.

№№№№№№

Диференціальним рівнянням з відокремлюваними змінними називається рівняння вигляду:

Щоб розв’язати це рівняння, треба спочатку відокремити змінні:

а потім проінтегрувати обидві частини знайденої рівності:

№№№№№

Означення. Лінійним однорідним диференціальним рівнянням другого порядку із сталими коефіцієнтами називається рівняння вигляду:

(1),

де і - сталі величини.

Щоб визначити загальний розв’язок рівняння, складемо характеристичне рівняння (2), яке дістаємо з рівняння (1) заміною і на відповідні степені , причому сама функція замінюється одиницею.

Тоді загальний розв’язок диференціального рівняння будується залежно від коренів та характеристичного рівняння (2). Тут можливі три випадки.

Випадок 1. Корені та - дійсні і різні. У цьому випадку загальний розв’язок рівняння має вигляд:

(3)

Випадок 2. Корені та - дійсні і рівня: = = . Тоді загальний розв’язок рівняння записується так:

(4).

Випадок 3. Корені та - комплексно-спряжені : та . У цьому випадку загальний розв’язок рівняння записується так:

(5).

№№№№№№

Зображення комплексного числа у вигляді z = r℮^φі, де r >0, називається показниковою формою комплексного числа. Щоб записати комплексне число z= а+ві в показниковій формі, треба знайти модуль цього числа; одне із значень аргументу цього числа.

Тригонометричну форму комплексного числа z = r(cosφ + isinφ) можна замінити показниковою формою z = r℮^φі.

Дії над комплексними числами, заданими в показниковій формі.

- добуток z₁ i z₂ :

- частку знаходять так:

- при піднесенні до степеня:

- для добування кореня використовують формулу:

№№№№№

Означення. Визначником (детермінантом) другого порядку для системи двох рівнянь із двома невідомими називають число і записується так: .

Визначником третього порядку для системи трьох рівнянь з трьома невідомими 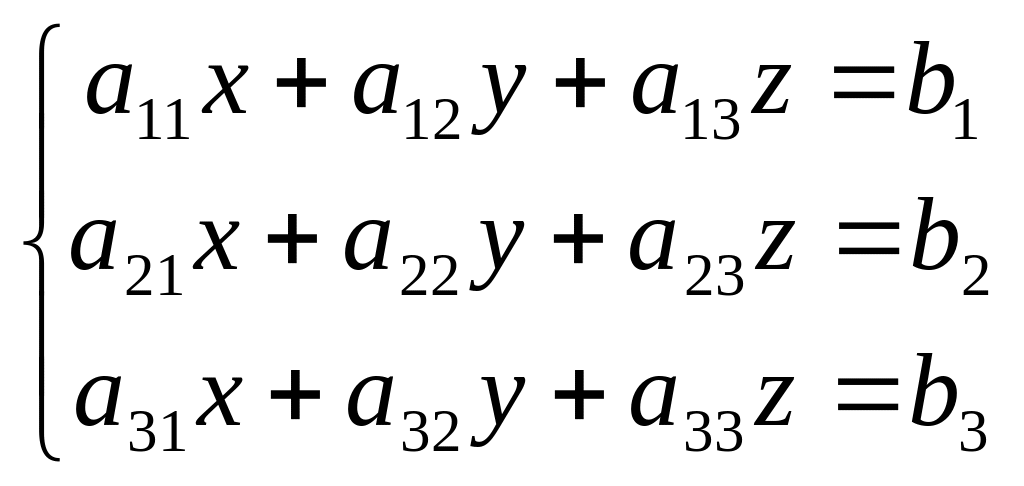записується так: 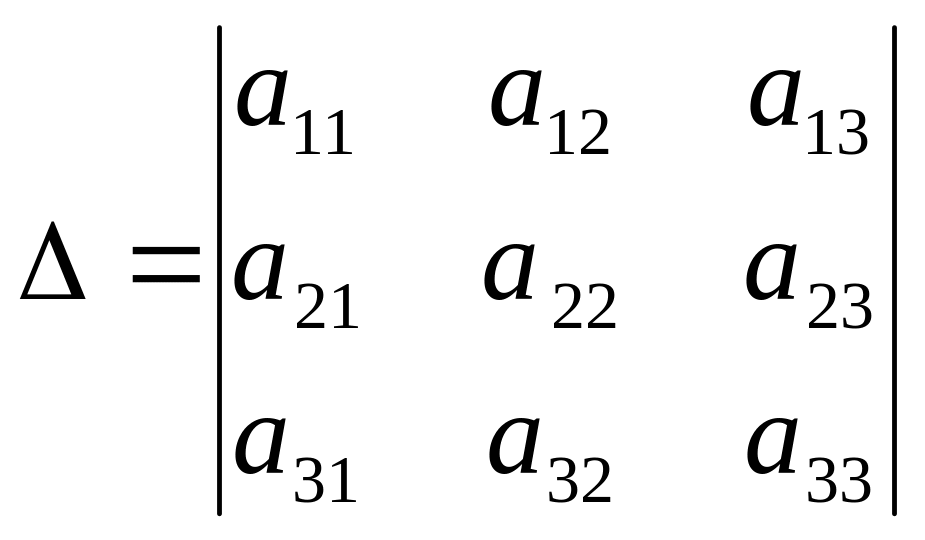і обчислюється за правилом трикутників: .

Властивості визначників.

1. Величина визначника не зміниться, якщо його рядки зробити стовпцями, а стовпці – рядками, не змінюючи нумерації їх.

2. Якщо помножити всі елементи деякого стовпця (або рядка) на те саме число k, то значення визначника також помножаться на те саме число k.

3. Якщо у визначнику поміняти місцями рядки або стовпці, то визначник змінить знак на протилежний.

4. Якщо елементи двох рядків або стовпців однакові, то визначник дорівнює нулю.

5. Величина визначника не змінюється, якщо до елементів одного рядка або стовпця додати елементи другого рядка або стовпця, помножені на те саме число.

№№№№№№

Означення. Матрицею розміру m x n або ( m x n) - матрицею називається прямокутна таблиця з чисел , і = 1,2, ..., n; j = 1,2, ..., n , вигляду:

,

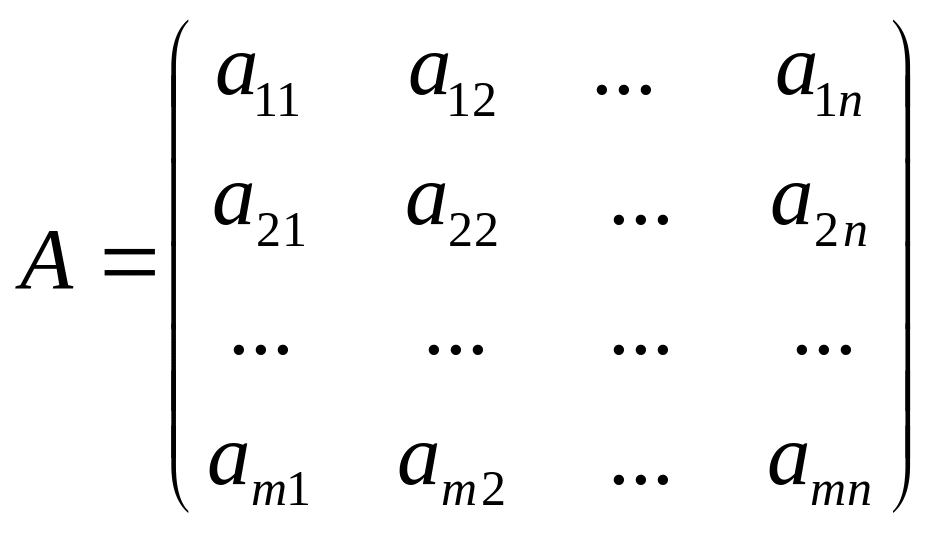яка складається з m рядків і n стовпчиків. Якщо m = n, то матриця називається квадратною; якщо m = 1, то маємо матрицю – рядок; якщо n = 1 – матрицю – стовпчик.

Означення. Сумою А+В (m × n) – матриць А = ( ) і В = ( ) називається матриця С = ( ) того самого розміру, кожний елемент якої дорівнює сумі відповідних елементів матриць А і В:

c i j = a i j + b i j , і = 1.2,…,m; j = 1.2,…,n..

Означення. Добутком λ А матриці А = ( ) на число λ Є R називається матриця

, яка одержується з матриці А множенням усіх її елементів на λ : = λ , і = 1.2,…,m; j = 1.2,…,n..

Означення. Добутком АВ ( т × п) – матриці А = (a_ij) на (п × k) – матрицю В = (b_ij) називається (m × k) – матриця С = (с_ij ), елемент якої с I j, що стоїть в i- му рядку та j - му стовпчику, дорівнює сумі добутків відповідних елементів i- го рядка матриці А та j- го стовпчика матриці В:

c_ij = a_i1b_1j + a_i2b_2j + ... + a_inb_nj, і = 1.2,…,m; j = 1.2,…,n..

№№№№№

Векторним добутком вектора на вектор називається такий третій вектор , який задовольняє умови:

1) абсолютна величина чисельно дорівнює площі паралелограма, побудованого на векторах ,

2) вектор перпендикулярний до площини цього паралелограма.

Абсолютна величина (модуль) векторного добутку обчислюється за формулою:

, де кут кут між векторами , .