Кручение бруса прямоугольного сечения

Теория кручения бруса прямоугольного профиля выходит за рамки курса сопротивления материалов, поэтому ограничимся основными её ре-

-зультатами. В угловых точках поперечного сечения бруса (рис. 4) каса-

-тельные напряжения отсутствуют, так как наличие касательных напря-

-жений противоречит закону их парности. В точках принадлежащих внешней поверхности бруса напряжения направлены вдоль соответству-

-ющей стороны сечения и достигают максимума в серединах сторон,при-

-чём наибольший максимум будет на большей стороне. Относительный

угол закручивания бруса и наибольшее касательное напряжение (на

длинной стороне) определяются по формулам:

Ɵ = Mz /( G* Jk) ; Tmax = Mz / Wk , где

Wk = α* H*B**2 ; Jk = β*H*B**3.

Максимальное напряжение на короткой стороне T’max = γ* Tmax.

Коэффициенты α, β и γ определяются из таблицы ( рис.4) и зависят от

параметра ϛ = H / В .

Рис.4.

Кручение бруса тонкостенного открытого профиля

Такой профиль можно рассмотреть как совокупность отдельно взятых

полос, которые при кручении бруса закручиваются на один и тот же

относительный угол Ɵ (рис.4С). Тогда общий крутящий момент будет (3)

Мz =Ɵ*G*∑ Jki , где Jki = ⅓ Hi*ti**3,

Откуда

Ɵ = Mz / (G*∑ Jki)

Тогда момент, воспринимаемый отдельно взятой j - й полосой, будет

Mzj = Ɵ*G* Jkj = Mz* Jkj / ∑ Jki.

При этом, максимальное касательное напряжение в этой полосе:

Tj = Mzj / Wkj , где Wkj = ⅓ H*t**2 ,

или

Tj = (Mz* Jkj / Wkj) / ∑ Jki = Mz*t j / ∑ Jki (6)

Как следует из формулы ( 6) расчетное напряжение будет в полосе, которая имеет наибольшую толщину t max :

Tmax = Mz*tmax / ∑ Jki ; (7)

или

Tmax = Mz / Wk, где Wk = ⅓*∑ Hi*ti**3/ t max. (7’)

Кручение бруса тонкостенного замкнутого профиля

Брус считается тонкостенным, если толщина стенки “t” cущественно мень-

-ше остальных размеров его поперечного сечения. Линия, которая делит

толщину сечения пополам, называется контуром сечения. В данном слу-

-чае контур сечения представляет собой замкнутую линию любой кон-

-фигурации. Толщина стенки может изменяться вдоль линии контура по

произвольному закону. Считаем, что касательное напряжение направлено вдоль линии контура и равномерно распределено по толщине. Такой брус, скручиваемый моментом Mz, приведен на рис.(5А) . Вырежем элемент двумя продольными сечениями, нормальными к контуру сечения, и двумя поперечными сениями, и рассмотрим условие его равновесия ( рис. 5B).

∑ Fz = T2* t 2 - T1*t1 = 0 , откуда T*t = Const,

То есть «поток» касательных напряжений вдоль контура сечения является постоянным. Рассмотрим момент касательных сил, действующих на эле-

-мент контура длиной ds относительно некоторого центра О, (рис. 5C):

dMz = T*t*ds*h =(T*t)*2d Ω (▲AOB )

где последнее выражение есть произведение потока касательных напря-

-жений на удвоенную площадь треугольника АОВ. Суммируя элеметар-

-ные моменты при полном обходе контура, получим:

Mz = 2*(T*t)*$dΩ = T*t*(2*Ω конт ).

Из полученного равенства определим напряжение в любой точке контура:

T = Mz / (2*t*Ωконт ), (8)

где Ωконт - площадь, ограниченная замкнутым контуром сечения.

Максимальное напряжение будет в точке контура, где толщина стенки

минимальна:

Tmax = Mz / ( 2*tmin*Ωконт). (8’)

Для определения относительного угла закручивания бруса следует при-

-равнять работу момента Mz при закручивании участка бруса длиной dz

к потенциальной энергии его деформации. Предварительно определим по-

-тенциальную энергию деформации элемента бруса ( рис. 5D), как полу-

-произведение силы, действующей на верхней грани, на смещение (сдвиг)

этой грани:

dU =1/2*(T*t*ds)*Г*dz = ½*( T**2*t*ds*dz)/ G , т.к. Г = Т/ G.

Выражая T по формуле (8) получим:

dU = ½*(Mz**2*dz*ds / (4*Ωконт**2*t)

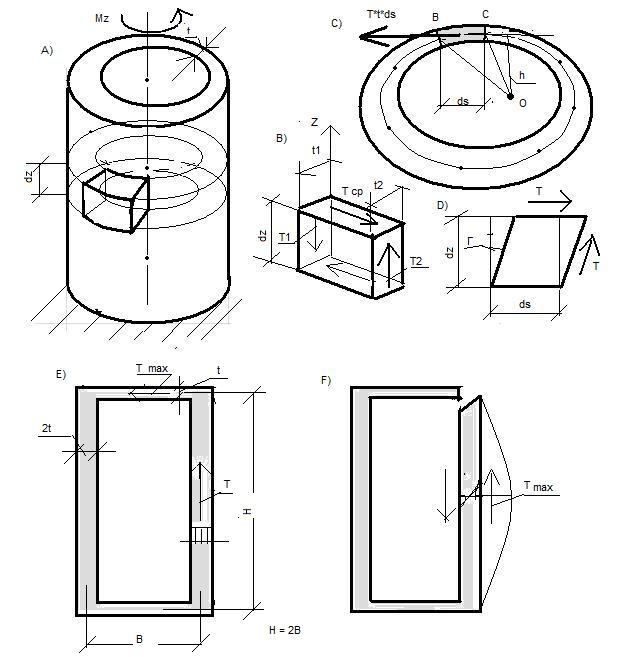
Рис. 5.

Работа внешнего момента будет:

A = ½*Mz*Ɵ*dz

Потенциальная энергия участка бруса определяется, как интеграл по контуру:

U =1/2*[(Mz**2*dz) /(4* Ωконт**2*G)]*$ ds/t.

Приравнивая А = U , получим:

Ɵ =(Mz*$ ds /t) / (4*Ωконт**2*G) (9)

Приведем формулы (8’) и (9) к стандартному виду:

Tmax =Mz / Wk ; Ɵ = Mz / GJk, где

Wk = 2*Ω*tmin ; Jk = 4*Ωконт**2/ $ ds/t, где

Wk – коэффициент сопротивления кручению; Jk – геометрический фактор

жёсткости сечения при кручении.

Определим величины Wk и Jk для сечения замкнутого контура (рис 5Е) и сечения открытого профиля, образованного из заданного путём прдольного распила (рис 5 F); примем H =2B; t = 0,1 B.

ЗАМКНУТЫЙ КОНТУР.

Wk =2*(H*B)*t = 2*2B*B*0,1B =0,4B**3;

Сначала определим $ ds/ t = 2*( H/ 2t + B/ t) =2*(2B/ 0,2 B + B/ 0,1 B) =40;

Jk =4*( H*B)**2/ 40 = 4*(2B**2)**2/40 = 0,4 B**4.

ОТКРЫТЫЙ ПРОФИЛЬ

Jk = ∑ Jki =2*[ ⅓ H*(2t)**3 +⅓ B*t**3] = ⅔ [ 2B*(0,2B)**3 + B*(0,1B)**3]= =0,0113*B**4.

Wk =Jk/ t max = 0,0113*B**4 / 0,2 B =0,057*B**3.

Таким образом крутильная жёсткость сечения замкнутого контура примерно в 35 раз, а расчётное напряжение примерно в 7 раз, превышают аналогич-

-ные показатели сечения открытого контура.

Таблица 1.

МОМЕНТ СОПРОТИВЛЕНИЯ И ГЕОМЕТРИЧЕСКИЙ ФАКТОР ЖЁСТКОСТИ

ДЛЯ ОСНОВНЫХ ВИДОВ ПОПЕРЕЧНЫХ СЕЧЕНИЙ ПРИ КРУЧЕНИИ.

_____________________________________________________________________

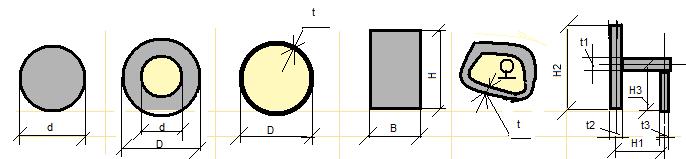
C=d/D

WK	Пd**3/16	ПD**3/16(1-C**4)	ПD**2*t/2	α*H*B**2	2*Ω*tmin	Jk/t max
JK	Пd**4/32	ПD**4/32(1-C**4)	ПD**4*t/4	β*H*B**3	4*Ω**2/$ds/t	⅓∑H*t**3

ПРИМЕР №1

Раскрыть статическую неопределимость. Построить эпюры Мz, Tmax , Ҩz ( рис. 6).

Задача является статически неопределимой, поскольку опорные моменты невоз-

-можно определить из уравнений статики: одна из опор (например, правая) будет лишней. Заменяя правую опору реактивным моментом Х, определяем кру-

-тящий момент на отдельных участках, согласно методу сечений:

Mz(AB) =3M –X ; Mz(BC) = M – X ; Mz(CD) = - X. (10)

Опорный момент Х определяется из условия равенства нулю угла поворота сечения D, который равен сумме углов закручивания участков бруса:

ҨD =ΔҨ(AB) +ΔҨ(BC) +ΔҨ(CD) =0.

Выражая ΔҨ по формуле (5), с учетом (10), получим:

(3M – X)*L/GJp(AB) + (M –X)*L/GJp(BC) – X*(0,5 L)/GJp(CD) =0. (10)

Согласно таб. 1 , приближенно считая Пd**4/32 = 0,1 d**4 :

Jp(CD) = 0,1 d**4; Jp(BC) = 0,1*(1,4 d)**4 = 0,4 d**4 ; Jp(AB) = Jp(AB)*(1 – 0,7**4) = 0,3 d**4.

Решая уравнение (10), после подстановки Jp и сокращения на L/Gd**4, получим

Х = 1,16 М, откуда Mz(AB) =1,84 M ; Mz(BC) = - 0,16 M ; Mz(CD) = - 1,16 M.

Определяем полярные моменты сопротивления участков бруса:

Wp(CD) = 0,2 d**3; Wp(BC) =0,56 d**3 ; Wp(AB) = Wp(BC)*(1 – 0,7**4) = 0,43 d**3

Вычисляем максимальные касательные напряжения по участкам бруса:

T(AB) = 1,84 M/ 0,43 d**3 = 4,28 M/ d**3;

T(BC) = - 0,16 M/ 0,56 d**3 = - 0,28 M/ d**3;

T(CD) = - 1,16 M/ 0,2 d**3 = -5,8 M/ d**3

Вычисляем углы поворота поперечных сечений бруса:

ҨВ = ΔҨ(АВ) = 1,84 М*L/ 0,3 Gd**4 = 6,2 ML/Gd**4

ҨC = ҨB +ΔҨ(BC) = 6,2 ML/Gd**4 – 0,16 ML/(G* 0,4 d**4) = 5,8 ML/Gd**4

ҨD = ҨC +ΔҨ(CD) = 5,8 ML/Gd**4 – 1,16 M*(0,5 L)/(G*0,1 d**4) = 0.

Эпюры Mz , Tmax , Ҩz приведены на рис.6. При построении эпюры Ҩz сначала

проставляются точки, соответствующие ординатам «контрольных» сечений A, B,

C, D, после чего эти точки соединяются прямолинейными отрезками.