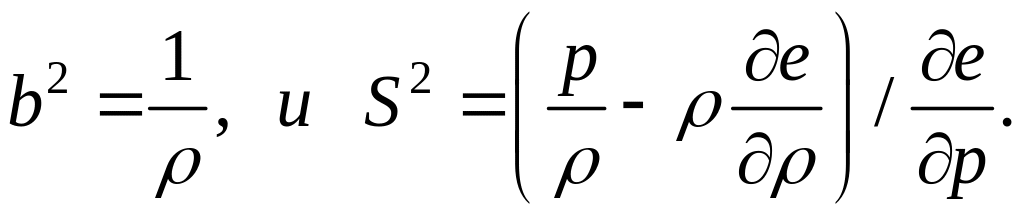1.2. Уравнения в безразмерном виде. Понятие о критериях подобия

Теория подобия является одним из наиболее эффективных методов, используемых в математической физике. Смысл законов подобия состоит в том, что они позволяют сворачивать большие многообразия решений в более узкие, подобные группы.

Далее будет использован один из подходов к выводу законов подобия – это непосредственное приведение уравнений, начальных и граничных условий задачи к безразмерному виду путем отнесения входящих в них величин к характерным масштабам задачи.

Для задач внешнего обтекания все газодинамические переменные отнесем к их значениям в невозмущенном потоке и характерному размеру тела. Тогда в качестве безразмерных переменных используем следующие (см.[14]):

,

где черточки над функциями относятся к размерным величинам.

В качестве примера построим в безразмерных переменных

одномерную систему уравнений Навье-Стокса.

Учитывая уравнения (8), запишем одномерную систему в следующем виде:

и вектор потока

В полной записи:

Упростим второе уравнение системы. Для этого умножим первое уравнение на величину u и вычтем его из преобразованного второго уравнения:

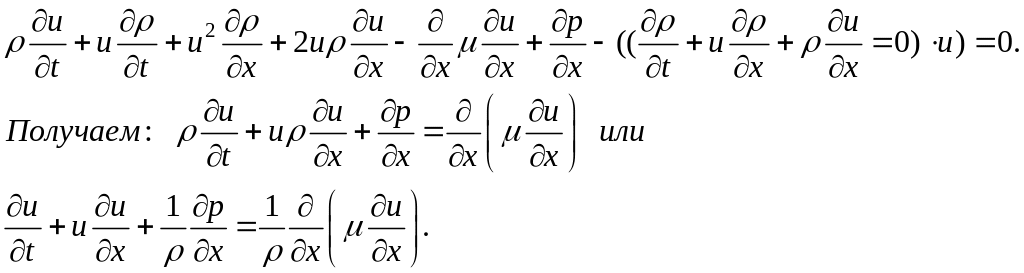
Для упрощения третьего уравнения системы, умножая первое уравнение на величины и соответственно и по очереди отнимая от третьего уравнения, а затем от оставшейся части третьего уравнения отнимая второе умноженное на величину , получим

. Таким образом, упрощенная одномерная система уравнений Навье – Стокса получается следующая:

( 11)

Замечание. Все уравнения записаны в размерных переменных. Черточки опущены по умолчанию.

В безразмерных переменных преобразованная одномерная система уравнений (11) примет вид:

(12)

Задача обтекания геометрически подобных тел, одинаково ориентированных к внешнему потоку, содержит три безразмерных критерия подобия:

Замечание. Одним из важных критериев подобия является число Маха. Число Маха характеризует отношение местной скорости газа к скорости звука и наряду с числом Рейнольдса определяет качественный характер течения. Число Маха имеет и математический смысл, оно определяет вид исследуемого уравнения. Если нестационарные уравнения газовой динамики имеют гиперболический вид, то стационарные уравнения являются гиперболическими в сверхзвуковой области (при М>1) и эллиптическими – в дозвуковой (при М<1).

1.3. Переход к недивергентным формам записи системы уравнений Навье-Стокса

При использовании дивергентной формы записи

(уравнение (8)) искомый вектор состояния течения находится в массовых переменных, как комбинация газодинамических параметров. Это не всегда удобно. Для нахождения самих параметров течения переходят к другим формам представления исходной системы.При этом, как правило, теряется дивергентность, но для гладких решений точность вычислений не ухудшается.

Рассмотрим новый вектор состояния потока , взаимообратный к вектору . Перейдем в уравнении (8) к вектору по формуле: 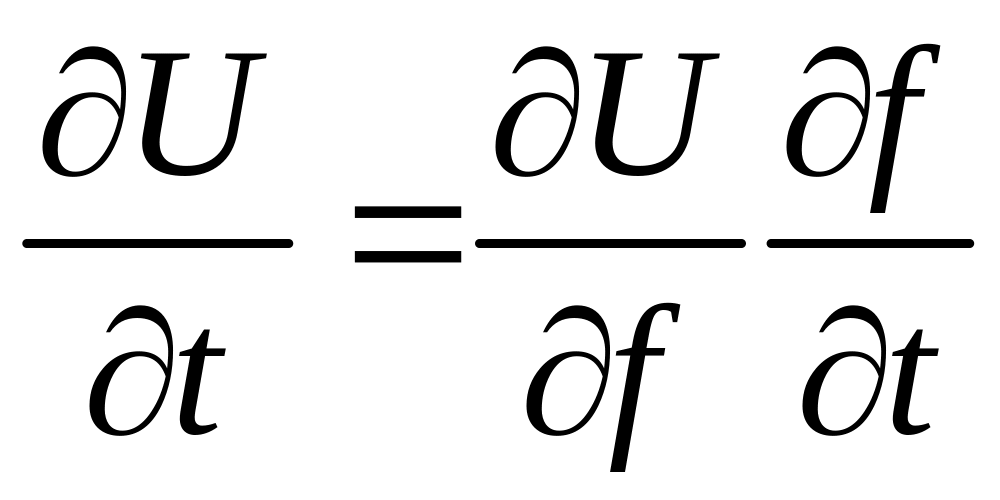. Здесь матрица есть матрица Якоби, обратная к которой 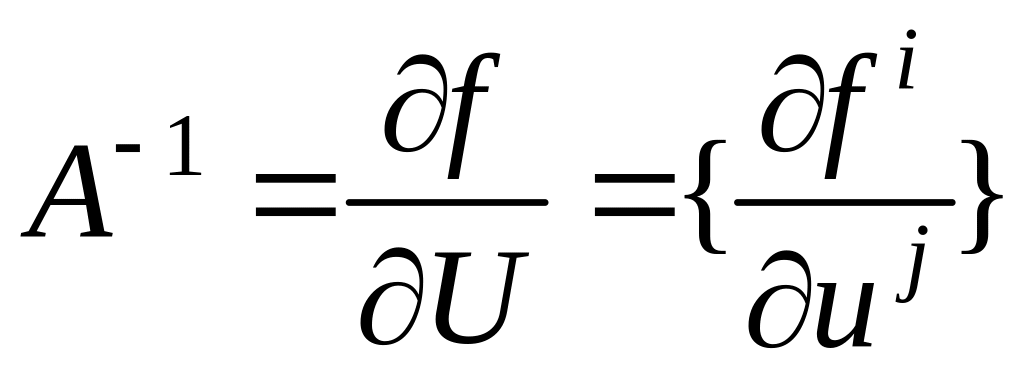. Умножим уравнение (8) на матрицу . Получим новую недивергентную форму представления системы уравнений

( см.[7]) :

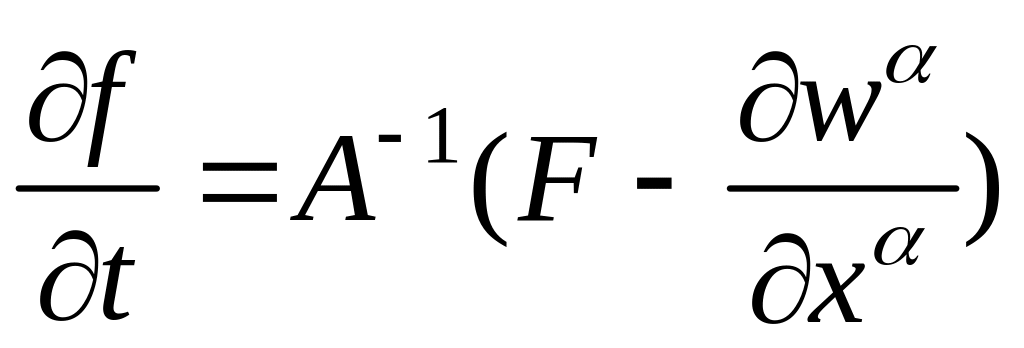. (13)

Рассмотрим более подробно производную от вектора потока. Сам вектор потока равен . Тогда

.

Например, если , то , тогда .

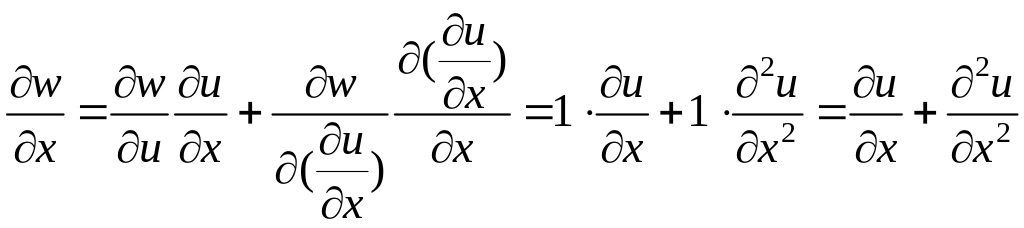Теперь полученное выражение для производной вектора потока подставим в уравнение (13):

и после преобразований получаем квазилинейное уравнение второго порядка (14)

Здесь .

Последняя система уравнений уже недивергентного вида. Рассмотрим три частных случая этой системы уравнений в зависимости от нового вектора состояния течения .

1. В случае, когда новый вектор потока равен

система уравнений

с искомым вектором преобразуется в

систему уравнений, для нахождения которой:

1) сначала находим матрицу Якоби и матрицу, обратную к ней

тогда

,

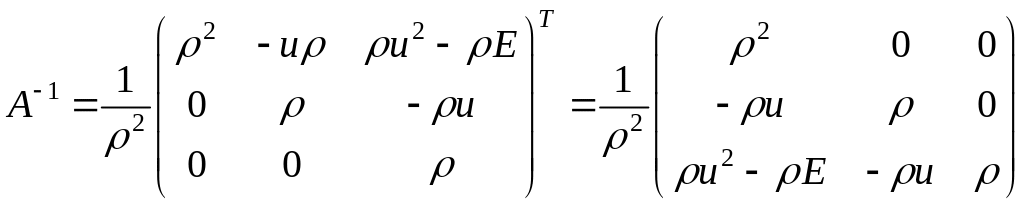2) дальше надо находить производные от вектора потока

(см.уравнение (11)): и И после вычислений получаем:

3) Для нахождения матрицы В недивергентной формы записи системы имеем:

.

Аналогично находится матрица С= и вектор правых частей .

Таким образом, в одномерном случае уравнение (14) с вектором течения получается следующее Здесь , а матрица В вычислена раньше.

Для нахождения коэффициентов системы уравнений недивергентной формы рассмотрим и другой способ решения. Он сводится к преобразованию уже полученной ранее дивергентной системы (11) с учетом нового вектора течения . Выпишем систему (11) :

(15)

Учитывая уравнение состояния , можно заменить производную давления во втором уравнении системы (15) по формуле . Тогда система преобразуется в следующую:

(16)

Выписывая теперь матрицу коэффициентов системы (16) при первых частных производных вектора течения , получаем

.

Матрица совпадает с вычисленной раньше матрицей В.

Из системы (16) также можно выписать и другие коэффициенты:

.

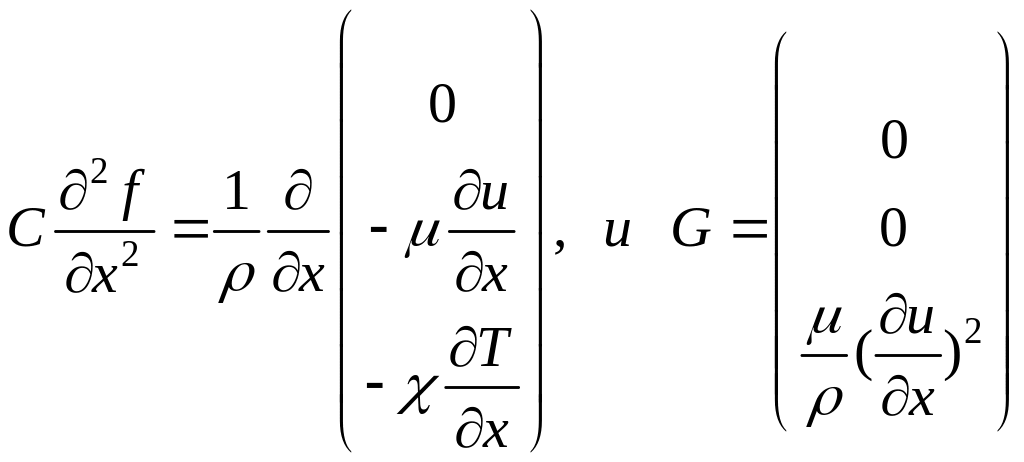В многомерном случае, когда новый вектор состояния течения равен , аналогично одномерному случаю, получаем первый матричный коэффициент недивергентной формы записи системы (14):

.

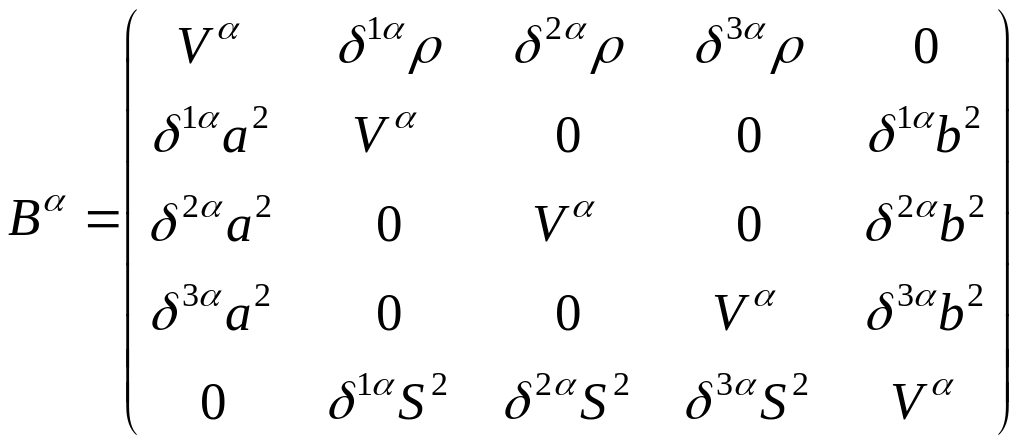Здесь коэффициенты 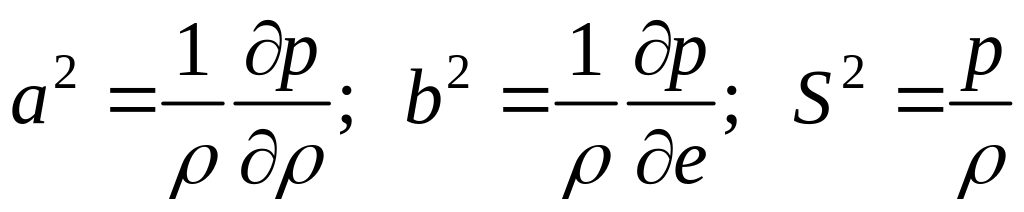и символы Кронекера. Другие коэффициенты недивергентной системы равны:

где диссипативная функция, вычисляемая по формуле:

2. Рассмотрим другой случай, когда новый вектор течения ищется в переменных: , . В этом случае меняются коэффициенты и . Из уравнений состояния и находим ,

. Заменяя градиент давления во втором уравнении системы (16), получаем: 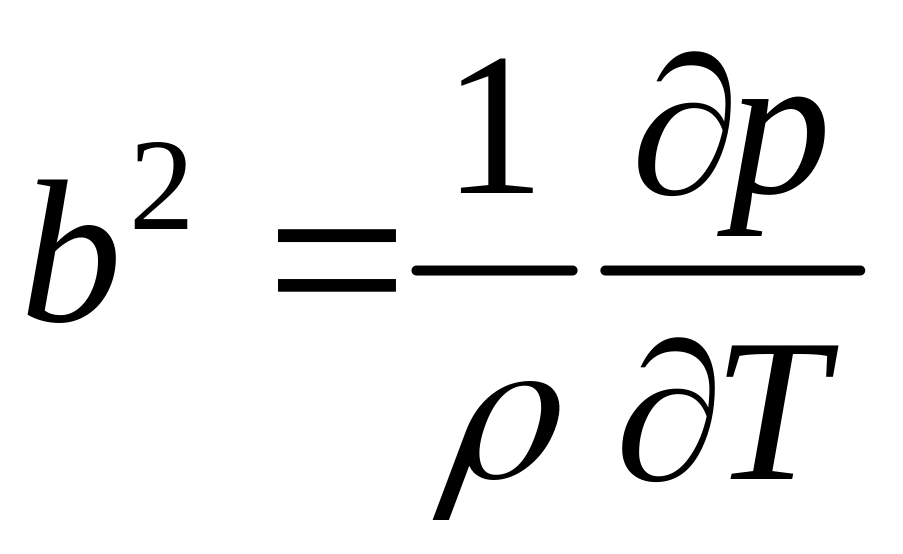. В уравнении энергии заменяем производные и, используя уравнение неразрывности преобразуем его к виду:

. Тогда для нового вектора течения матрица

. Здесь = .

3. В третьем случае, когда новый вектор течения , , после преобразований получаем матрицу

Здесь