2.9. Схема с несогласованным стабилизирующим оператором

При аппроксимации дифференциальных операторов вида несимметричными разностными операторами получаются разностные схемы, которые реализуются пятиточечными скалярными прогонками. Для получения стационарного решения методом установления можно использовать схемы, в которых порядок аппроксимации членов в стабилизирующем операторе отличается от порядка аппроксимации членов оператора правой части. При установлении порядок аппроксимация разностной схемы определяется по порядку аппроксимации правой части. Это различие позволяет строить разностные схемы, которые реализуются трехточечными прогонками (см.[6]).

Рассмотрим систему уравнений Навье-Стокса для сжимаемого теплопроводного газа записанную в следующем недивергентном виде.

. (46)

Для ее аппроксимации выберем факторизованную разностную схему

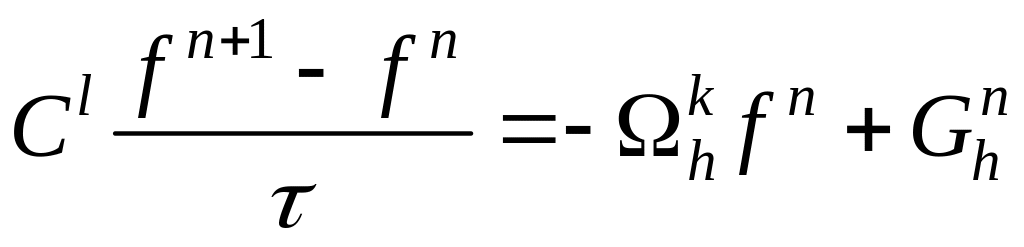(47)

со стабилизирующем оператором .

Здесь разностные операторы

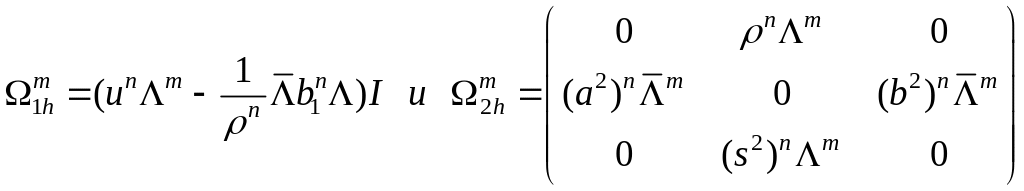,где

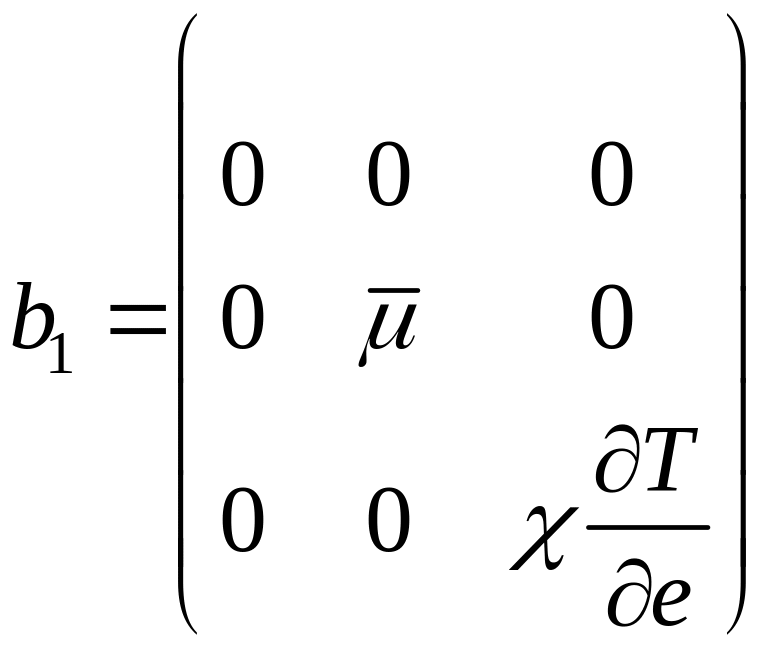и .

Заметим, что m = .

Схема (47) на каждом дробном шаге решается -точечными прогонками и погрешность ее аппроксимации есть

, а при установлении . Здесь – порядок аппроксимации членов стабилизирующего оператора, а –

порядок аппроксимации членов оператора правой части.

Определение. Оператор называется согласованным, если и несогласованным, если .

Рассмотрим разностную схему с несогласованным оператором при . На каждом дробном шаге ее решение может быть получено трехточечной прогонкой и при установлении схема имеет порядок аппроксимации . Эта схема по-прежнему остается безусловно устойчивой, но запас устойчивости ее уменьшается.

Покажем ее безусловную устойчивость для уравнений газовой динамики. В этом случае характеристическое уравнение схемы следующее:

где и .

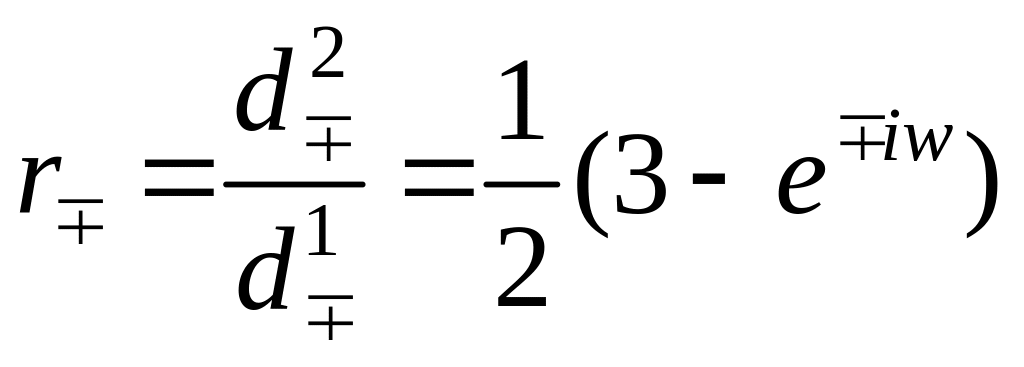Один из корней характеристического уравнения равен

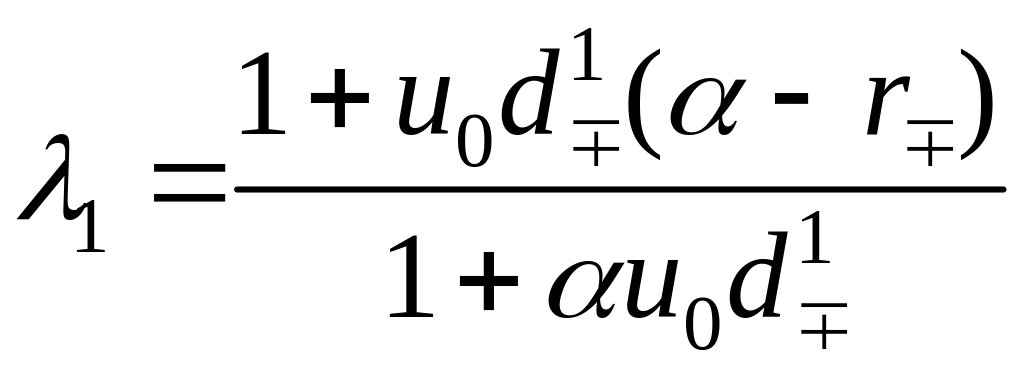. Тогда , если .

Два других оставшихся корня находим при в предельных случаях, когда – гиперзвуковое течение. В этом случае корни характеристического уравнения . И во втором случае, когда – медленные течения. Здесь характеристическое уравнение может быть записано в виде

, где

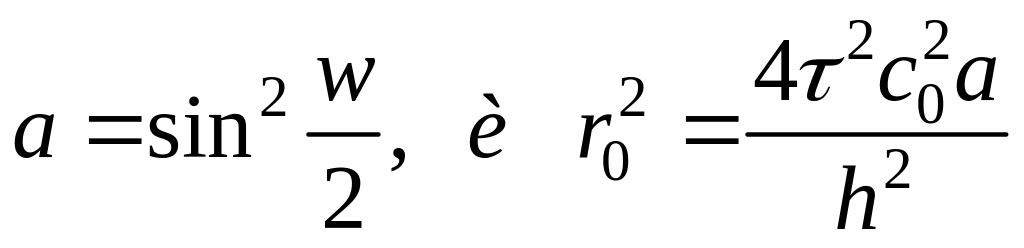. Его корни равны .

Таким образом, разностная схема (47) безусловно устойчива

при в случае согласованного стабилизирующего оператора

и при в случае несогласованного стабилизирующего

оператора.

В многомерном случае схема приближенной факторизации с несогласованным стабилизирующим оператором становится условно устойчивой.

2.10. Схемы для решения стационарных задач

При решении стационарных задач уравнений газовой динамики и Навье-Стокса используется два подхода:

1. непосредственное интегрирование системы стационарных уравнений,

2. интегрирование некоторой аппроксимирующей системы, решение которой стремится к решению исходной стационарной системы.

Использование первого подхода приводит, в одномерном случае, к интегрированию систем нелинейных обыкновенных дифференциальных уравнений. В многомерном случае получается уже система уравнений в частных производных, тип которых зависит от режима течений. Как правило, для уравнений газовой динамики при сверхзвуковом течении - система гиперболического типа, а при дозвуковом – эллиптическая. Для параболизированных систем уравнений Навье-Стокса – системы параболического или эллиптического типов соответственно.

Решение уравнений, особенно эллиптического типа, представляет значительные трудности. Поэтому для решения стационарных систем экономичнее использовать второй подход, основанный на итерационных методах. В уравнения добавляют итерационное слагаемое, временной параметр является итерационным, и методом установления решается система уравнений, которая сходится к исходной системе.

Такой метод хорош и тем, что он используется для любого типа течений.

Рассмотрим применение этого метода на примере модельных уравнений.

Для решения уравнения

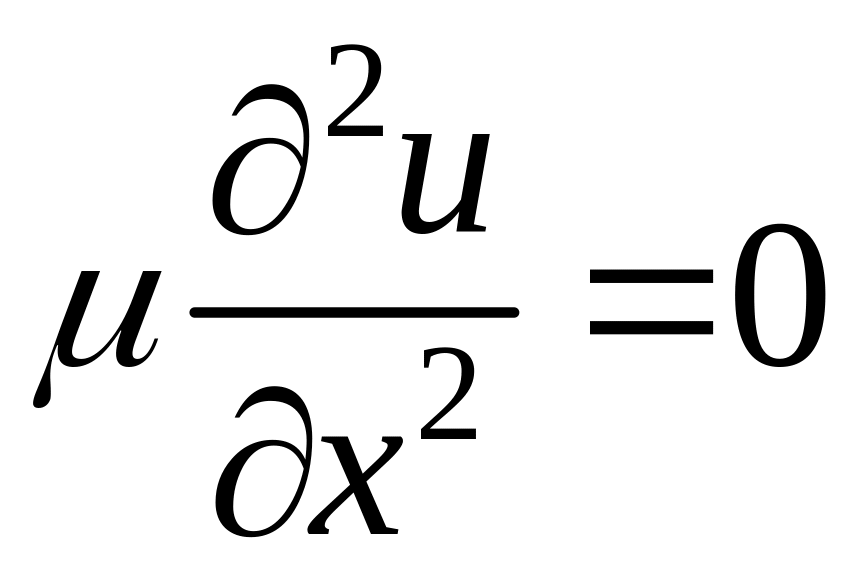(48)

с заданными граничными условиями воспользуемся следующей итерационной схемой ( – номер итерации )

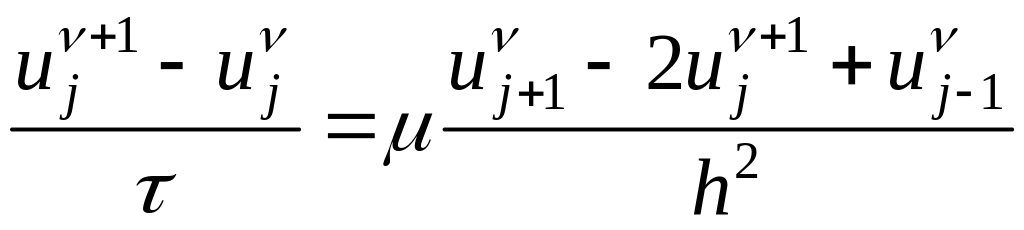(49)

При сходимости итераций (когда ) схема (49) при установлении аппроксимирует уравнение (48) с порядком .

Итерационная схема (49) аппроксимирует (48) уже при установлении, а на промежуточных итерациях схема аппроксимирует другое уравнение. Действительно, если к числителю дроби, стоящей в правой части схемы (49) прибавить и отнять выражение , то получим следующую схему:

которая на каждом промежуточном шаге схема аппроксимирует уравнение:

.

Схема (49) безусловно устойчива. Устойчивость исследуем методом гармоник. При решении характеристического уравнения

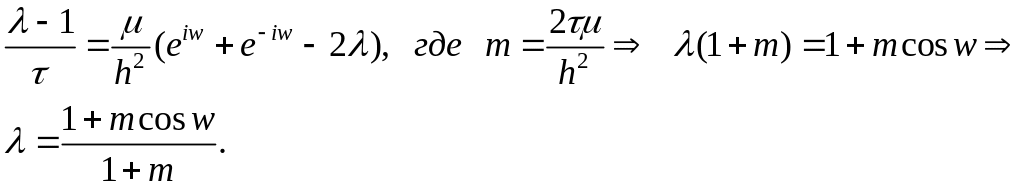
Получаем, что , так как .

Расчет по схеме (49) проводится по явной формуле:

.

Можно строить модификации схемы (49), которые тоже являются безусловно устойчивыми, например схема:

,

Здесь численный счет ведется по неявной схеме бегущего счета.

В работе (см.[15]) предложена следующая схема для решения уравнения теплопроводности с использованием метода расщепления:

(50)

Переписывая схему (50) в виде

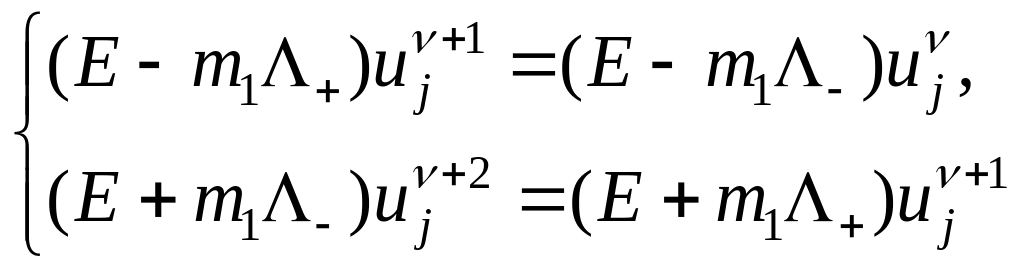(51)

и после исключения промежуточного слоя приходим к разностному уравнению

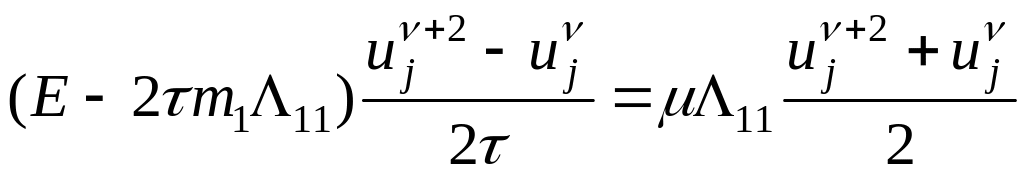. Здесь .

Полученная схема аппроксимирует при установлении уравнение (48) со вторым порядком точности по времени и является безусловно устойчивой.

Каждое уравнение системы (51) реализуется по схеме бегущего счета: первое уравнение – справа налево, а второе наоборот слева направо.

Рассмотрим итерационную схему решения и нелинейного уравнения

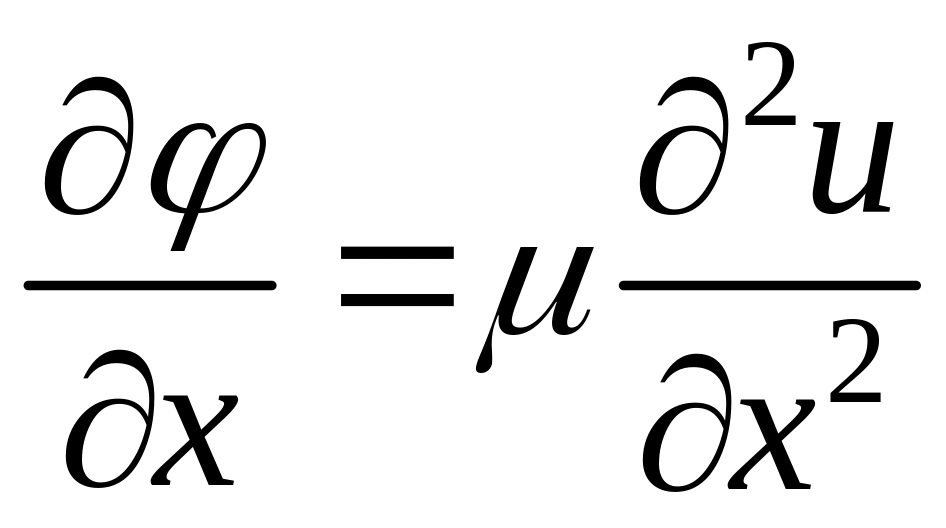, где . (52)

Добавляем итерационное слагаемое

.

При установлении схема аппроксимирует уравнение (52) с порядком и после линеаризации вектора может численно решена по схеме бегущего счета.