
- •Тухбатуллина Диляра гр.4109
- •Глава 1. Множества, отношения и функции.
- •1. Это процедура, которая, будучи запущенной, порождает некоторые объекты по заданным правилам.
- •4. Фундаментальное неопределяемое понятие.
- •3. Каждый элемент которого есть элемент в, но не а.
- •4. Упорядоченных пар (а,b), таких, что а а и b b.
- •3. Порождающей процедурой.
- •Глава 2. Алгебраические структуры.
- •Глава 3. Булевы функции.
- •Глава 4.
- •Глава 5.
- •Глава 2.
- •Глава 3 Булевы функции.
- •Глава 4.Элементы комбинаторики.
- •Глава 5.Теория графов.
- •Глава 1
- •12. Упорядоченной парой называется
- •Глава 2
- •14)Упорядоченной парой называется:
- •Глава 3 Булевы функции.
- •Глава 4.Элементы комбинаторики.
- •Глава 5.Теория графов.
- •§1. Задание множества.
- •§2. Операции над множествами.
- •§3. Разбиение множества. Декартово произведение.
- •§4. Отношения.
- •Подмножество r декартового произведения а в;
- •Подмножество r декартового произведения а в
- •Порождающей процедурой
- •§5. Операции над отношениями.
- •§6. Функции.
- •§7. Отношение эквивалентности. Фактор-множество.
- •§8. Отношения порядка.
- •Глава 2. Алгебраические структуры.
- •§1. Операции и предикаты.
- •§2. Алгебраическая система. Алгебра и модель.
- •§3. Подалгебры.
- •§4. Морфизмы алгебр.
- •§5. Алгебра с одной операцией.
- •§6. Группы.
- •§7. Алгебра с двумя операциями. Кольцо.
- •8. Кольцо с единицей.
- •§9. Поле.
- •§10. Решетка.
- •§11. Булевы алгебры.
- •§12. Матроиды.
- •Глава 3. Булевы функции.
- •§1. Основные булевы функции.
- •§2. Формулы.
- •§3. Упрощения в записях формул.
- •§4. Равносильность формул.
- •§5. Важнейшие пары равносильных формул.
- •§6. Зависимость между булевыми функциями.
- •§7. Свойства операций штрих Шеффера, стрелка Пирса и сложения по модулю два.
- •§8. Элементарные суммы произведения. Конституены нуля и единицы.
- •§9. Дизъюнктивные и конъюнктивные нормальные формы.
- •§10. Представление произвольной булевой функции в виде формул.
- •§11. Совершенные нормальные формы.
- •§12. Полином Жегалкина.
- •§12. Сокращенные дизъюнктивные нормальные формы.
- •§14. Метод Квайна получения сокращенной д.Н.Ф.
- •§15. Тупиковые и минимальные д.Н.Ф.
- •§16. Метод импликации матриц.
- •§17. Минимальные конъюнктивные нормальные формы.
- •§18. Полнота системы функции. Теорема Поста.
- •§19. Приложения теории булевых функции к анализу и синтезу контактных схем.
- •§20. Приложение теории булевых функции к анализу и синтезу схем их функциональных элементов.
- •§21. Функциональная декомпозиция.
- •Глава 4. Элементы комбинаторики.
- •§1. Правило суммы для конечных множеств.
- •§2. Правило произведения для конечных множеств.
- •§3. Выборки и упорядочения.
- •§4. Биноминальная теорема.
- •5. Число всевозможных разбиений конечного множества. Полиномиальная теорема.
- •§6. Метод включения и исключения.
- •§7. Задача о беспорядках и встречах.
- •§8. Системы различных представителей.
- •Глава 5. Теория графов.
- •§1. Основные типы графов.
- •§2. Изоморфизм графов.
- •§3. Число ребер графа.
- •§4. Цепи, циклы, пути и контуры.
- •§5. Связность графа. Компоненты связности.
- •§6. Матрица смежности.
- •7. Матрицы смежности и достижимости.
- •§8. Критерий изоморфизма графов.
- •§9. Матрица инциденций.
- •§10. Деревья.
- •3.Что такое порождающая процедура?
- •Глава 1.
- •Глава 2
- •Глава 3
- •59). Найдите сднф для функции заданной таблицей истинности:
- •60). Найдите скнф для функции заданной таблицей истинности:
Глава 1.
1). Множество – это …
А). n-ное количество каких-либо объектов.
Б). Процедура, порождающая объекты по заданным правилам.
В). Собрание определенных объектов, мыслимое как единое целое. +
Г). Предикат элементов числа.
2). Какую процедуру называют порождающей?
А). Которая, будучи запущенной, выявляет принадлежность объекта данному множеству.
Б). Которая, будучи запущенной, определяет все элементы данного множества.
В). Которая, будучи запущенной, определяет истинность высказывания.
Г). Которая, будучи запущенной, порождает нек. объекты по заданному правилу. +
3). Предикат это …
А). Случайные множества.
Б). Некоторое условие, выраженное в форме логического утверждения. +
В). Отношение элемента к определенному множеству.
Г). Все элементы определенного множества.
4). Будет ли пустое множество V каким-либо подмножеством некоторого множества?
А). Будет собственным подмножеством.
Б). Будет несобственным подмножеством. +
В). Не будет никаким подмножеством.
Г). Нет верного варианта ответа.
5). Какое множество называют конечным?
А). Множество, состоящее из конечного числа элементов. +
Б). Множество, в котором нет элементов.
В). Множество, границы которого не определены.
Г). Множество натуральных чисел.
6). Что называется объединением множеств А и В?
А). Множество С, каждый элемент которого является элементом А или В. +
Б). Множество С, каждый элемент которого является элементом А и В.
В). Множество С, каждый элемент которого есть элемент А, но не В.
Г). Множество С, каждый элемент которого есть элемент В, но не А.
7). Что называется пересечением множеств А и В?
А). Множество С, каждый элемент которого является элементом А или В.
Б). Множество С, каждый элемент которого является элементом как А, так и В. +
В). Множество С, каждый элемент которого есть элемент А, но не В.
Г). Множество С, каждый элемент которого есть элемент В, но не А.
8). Где представлено пересечение множеств?
А).
![]()
Б).
![]()
В).
![]() +
+
Г).
![]()
9). Вытекает ли из равенства А\В=С, что А=В∪С?
А). Да.
Б). Нет.
В). Вообще нет, но в частном случае да. +
Г). Нельзя применить обратные переходы.
10). Какой объект называется упорядоченной парой?
А). Объект (a, b) такой, что (a, b)=(c, d), причем a=c и b=d. +
Б). Объект (a, b) такой, что (a, b)≠(c, d), причем a=c и b=d.
В). Объект (a, b) такой, что (a, b)=(c, d), причем a≠c и b≠d.
Г). Объект (a, b) такой, что (a, b)=(c, d), причем a=c или b=d.
11). На каком рисунке представлена разность множества А?
А).
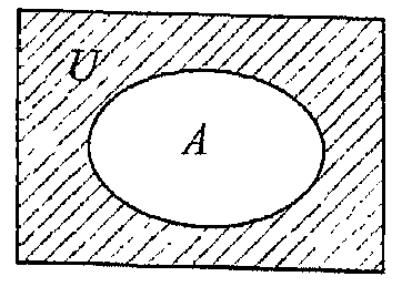
Б).
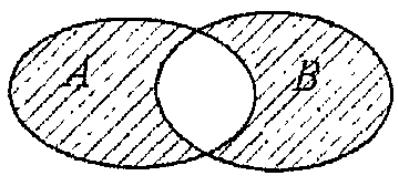
В).
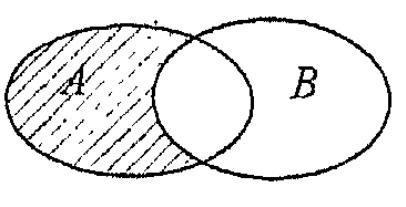 +
+
Г).
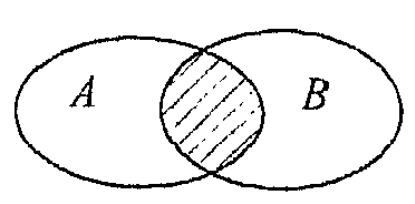
12). Что называется декартовым произведением двух множеств А и В?
А). Множество, элементами которого являются всевозможные упорядоченные пары элементов исходных множеств. +
Б). Область определения множеств А и В.
В). Обратное отношение множества А к множеству В.
Г). Обозначение элементов множеств на декартовом системе координат.
13). Что такое разбиение множества А?
А). Представление множества в виде объединения произвольного количества попарно непересекающихся подмножеств. +
Б). Представление множества в виде реляционной системы.
В). Представление множества в виде алгебраической системы.
Г). Представление множества в виде совокупности операций над элементами А.
14). Пусть А={а, b}, B={c, d}, тогда их декартово произведение равно:
А). {(a, а), (b, b), (c, c), (d, d)}.
Б). {(a, c), (b, c), (a, d), (b, d)}. +
В). {(a, b), (c, d), (b, a), (c, d)}.
Г). {(a, a), (b, c), (d, d), (c, b)}.
15).
Схематическим обозначением какой
операции можно назвать данный рисунок?
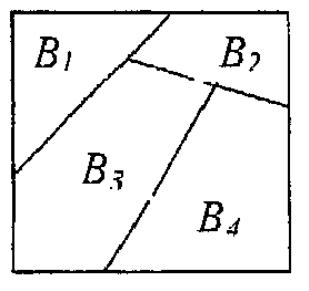
А). Разбиение множества. +
Б). Соединение универсума.
В). Декартова сумма подмножеств.
Г). Ни одну из операций нельзя обозначить данным рисунком.
16). Что называют бинарным отношением?
А). Подмножество декартового произведения двух множеств. +
Б). Разность двух множеств.
В). Отношение элементов одного множества к элементам обратного множества.
Г). Отношение количества элементов множества к её максимальному элементу.
17). Пусть задано подмножество R множества АхВ (аЄА, bЄВ). Как можно это записать?
А). Rab.
Б). aRb. +
В). abR.
Г). aRbR.
18). А={1,2,3,4}, aRb только при a<b. Выберите правильное задание этого отношения.
А). {(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)}. +
Б). {(1, 1), (2, 2), (3, 3), (4, 4)}.
В). {(1, 2), (1, 3), (1, 4)}.
Г). {(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4), (1, 1), (2, 2), (3, 3), (4, 4)}.
19). Чем нельзя задать R?
А). Предикатом.
Б). Порождающей процедурой.
В). Матрицей отношения.
Г). Можно всеми вышеперечисленными способами. +
20). Единичным отношением Е называется бинарное отношение на множестве А такое, что:
А). Е={(a, a): aЄA}. +
Б). А={(a, a): aЄЕ}.
В). Е={(a, a): aЄЕ}.
Г). А={(a, a): aЄA}.
21). Как записывается отношение R-1, обратное к R?
А). R-1={(b, a): a, bЄR}. +
Б). R-1={(a, b): a, bЄR-1}.
В). Любым из двух способов, указанных выше.
Г). Такого отношения не бывает.
22). Каким значком в математике заменяются слова «тогда и только тогда»?
А). <=>. +
Б). Ω.
В). ∑.
Г). ≤≡≥.
23).
Как принятой читать значок
![]() в
математике?
в
математике?
А). Для всех.
Б). Только для.
В). Существует. +
Г). Не существует.
24). Как правильно обозначить композицию R и S?
А). R◦S. +
Б). R≡S.
В). R↔S.
Г). R≈S.
25). Укажите в каком высказывании мы можем увидеть принцип Дирихле.
А). Если кролики рассажены в клетки, причём число кроликов больше числа клеток, то хотя бы в одной из клеток находится более одного кролика. +
Б). Если на Востоке встает солнце, значит сейчас на Западе наступает ночь.
В). Каждый охотник желает знать, где сидит фазан.
Г). Если всеразрушающее ядро влетит в ничем не рушимую стену, то произойдет принцип Дирихле.
26). На каком рисунке мы можем увидеть отношение «биекция»?
А).
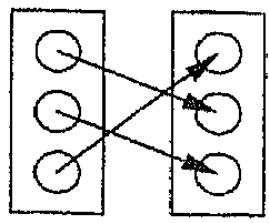 + Б).
+ Б).
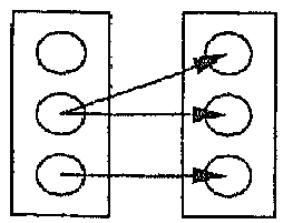 В).
В).
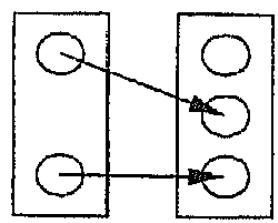 Г).
Г).
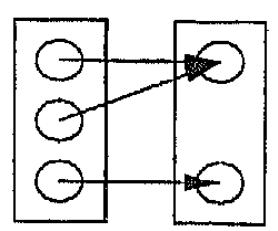
27). Какое из следующих утверждений истинно?
А). Композиция биективных функций является функцией биективной. +
В). Функция ƒ имеет обратную функцию ƒ-1 только тогда, когда ƒ инъективна и сюръективна.
Г). Оба утверждения верны.
Д). Оба утверждения неверны.
28). Укажите пример биективной функции.
А).
 + Б).
+ Б).
 В).
В).
 Г).
Г).
29). В каком случае бинарное отношение ƒ на множествах А и В, называется функцией?
А). Если образ каждого элемента единственен. +
Б). Если каждое из множеств конечно.
В). Если множества обозначены только предикатом.
Г). Если разность множеств равно пустому множеству.
30). Бинарное отношение R на множестве А называется отношением эквивалентности, если R:
А). Рефлексивно, транзитивно и симметрично. +
Б). Рефлексивно.
В). Транзитивно.
Г). Симметрично.
31). Какой из следующих примеров можно отнести к эквивалентному отношению?
А). 3<9.
Б). 5=5. +
В). 7≤8.
Г). 1>2.
32). Пусть R – отношение эквивалентности на множестве А, тогда верно, что:
А). Различные смежные классы не пересекаются.
Б). Объединение всех смежных классов совпадает со всем множеством А.
В). Верно только А.
Г). Верны оба суждения. +
33). Когда два целых числа a и b можно назвать сравнимыми по модулю m?
А). Если m делитель числа a – b. +
Б). Если a*m=b.
В). Если a/b=m.
Г). Если a+a=m.
34). Что из нижеперечисленного верно?
А). a≡a(mod m).
Б). a≡b(mod m) b≡a(mod m).
В). Верно только А.
Г). Верно А и Б. +
35). Бинарное отношение R на множестве A называется отношением частичного порядка, если R:
А). Рефлексивно, транзитивно и антисимметрично. +
Б). Рефлексивно.
В). Транзитивно.
Г). Антисимметрично.
36). Как называется множество А, с заданным на нём отношением частичного порядка?
А). Множество строгого порядка.
Б). Сравнимое множество.
В). Частично упорядоченное множество. +
Г). Несравнимое множество.
37). Какое частично упорядоченное множество можно назвать линейно упорядоченным множеством?
А). В котором любые два элемента сравнимы. +
Б). В котором любые два элемента несравнимы.
В). В котором все элементы равны между собой.
Г). Такого множества не существует в природе.
38). Укажите пример вполне упорядоченного множества.
А). (-∞, ∞).
Б). (-∞, 100].
В). {0, 1, 2, 3…}. +
Г). [0, ∞).
39). Что значит дискретная структура?
А). Неопределенная.
Б). Конечная. +
В). Мнимая.
Г). Иррациональная.
40). Какой элемент а частично упорядоченного множества А называется минимальным?
А). Если не существует такого х, что x<a. +
Б). а=0.
В). У такого множества нет минимального элемента.
Г). а минимально при условии, что он единственный элемент множества А.
