Глава 5. Теория графов.

§1. Основные типы графов.

255. Совокупность, состоящая из конечного множества V точек, называемых вершинами, и множества неупорядоченных пар различных вершин из V, называемых ребрами это

1. Граф;

2. Множество.

3. Мультиграф.

4. Псевдограф.

256. Граф называется помеченным, если его вершины

1. Отличаются одна от другой какими либо пометками;

2. Не различаются.

3. Имеют смежные вершины.

4. Нет правильных ответов.

257. Граф называется непомеченным, если его вершины

1. Отличаются одна от другой какими либо пометками.

2. Не различаются;

3. Имеют смежные вершины.

4. Нет правильных ответов.

258. В графе не может быть ребер, начинающихся и заканчивающихся в одной вершине, так называемых

1. Петель;

2. Узел.

3. Псевдограф.

4. Орграф.

259. Как называется совокупность, состоящая из конечного множества V точек, называемых вершинами, и множества упорядоченных пар различных вершин из V, называемых дугами?

1. Орграф;

2. Мультиграф.

3. Псевдограф.

4. Подграф.

260. Если два различных ребра х и у инцидентны одной и той же вершине, то они называются

1. Смежными;

2. Тривиальными.

3. Помеченными.

4. Непомеченными.

261. Граф, в котором вершины могут соединяться более чем одним ребром, называется

1. Мультиграф;

2. Псевдограф.

3. Ориентированный граф.

4. Подграф.

262. Граф, в котором есть дополнительные кратные ребра и петли, называется

1. Псевдограф;

2. Мультиграф.

3. Подграф.

4. Ориентированный граф.

263. Ориентированный граф, не имеющий симметричный дуг называется

1. Направленным оргграфом;

2. Смешанным графом.

3. Подграфом.

4. Объединением графов.

264. Граф, в котором имеются и дуги, и ребра, называется

1. Смешанным графом;

2. Направленным графом.

3. Орграфом.

4. Псевдографом.

265. Граф, состоящий только из вершин называется

1. Нуль-графом;

2. Петлей.

3. Орграфом.

4. Псевдографом.

266. Граф, в котором любые две вершины соединены ребром, называется

1. Полным;

2. Неполным.

3. Нуль-графом.

4. Смешанным.

267. Как называется граф G=(V’,X’), множество верщин V’ которого является подмножеством вершин V графа G, а ребрами (дугами) – часть ребер (дуг) графа G, оба конца котроых лежат в пространстве V’?

1. Подграф графа (орграф) G=(V,X);

2. Остовной подграф графа G=(V,X).

3. Дополнение графа (орграф) G=(V,X).

4. Смешанным графом.

268. Как называется граф G=(V,X*), Х* 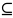Х, содержащий все вершины графа G=(V,X), но возможно не содержащий некоторых ребер из Х?

1. Подграф графа (орграф) G=(V,X).

2. Остовной подграф графа G=(V,X);

3. Дополнение графа (орграф) G=(V,X).

4. Смешанным графом.

269. Как называется граф (орграф) 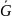=(V,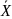 ) с тем е множеством вершин V, а 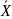является дополнением множества Х до множества всех неупорядоченных (упорядоченных) пар вершин из V?

1. Подграф графа (орграф) G=(V,X).

2. Остовной подграф графа G=(V,X).

3. Дополнение графа (орграф) G=(V,X);

4. Смешанным графом.

270. Как называется граф, множеством вершин которого является V=V₁ V_{2 ,} а множеством ребер является Х=Х₁ Х₂?

1. Подграф графа (орграф) G=(V,X).

2. Остовной подграф графа G=(V,X).

3. Дополнение графа (орграф) G=(V,X).

4. Объединением графов G₁=(V₁,X₁) и G₂=(V₂,X₂);

271. Если существует разбиение множества его вершин на две непересекающихся подмножеств V1 и V₂ так, что V=V₁ V₂ и каждое ребро графа G соединяет вершины из разных множеств, то такой граф G=(V,X) называется

1. Двудольным;

2. Полным двудольным.

3. Неполным двудольным.

4. Разбиением множества.

272. Если любая вершина из V₁ соединена ребром с каждой вершиной из V_2, следовательно, каждая вершина из V₂ соединена ребром с каждой вершиной из V_1, то такой двудольный граф называется

1. Двудольным.

2. Полным двудольным;

3. Неполным двудольным.

4. Разбиением множества.