Глава 2. Алгебраические структуры.
В функция f:AB множество А может быть
1. Ограниченной.
2. Упорядоченной.
+3. Любым;
4. Нет правильного ответа.
Если множество А является декартовым произведением n множеств, то аргументом функции f:AB является :
1. 0.
2. 1.
+3. Упорядоченная n-ка.
4. Нет правильного ответа.
Функцию
:
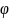СnC
называют:
1. Операцией следствия.
2. Операцией сложения.
3. Операций умножения.
+4. n-арной операций.
Продолжите «Предикат - это …..»
1. Функция.
2. Операция с аргументами.
+3. Логическое утверждение
4. Нет правильного ответа.
Предикат от n аргументов называется:
+1. Функция с областью определения и областью значения;
2. Функция с областью определения.
3. Функция с областью значения.
4. Нет правильного ответа.
Алгебраической системой называют:
1. Пустое множество А.
2. Множество предикатов.
+3. Непустое множество А с введенными на этом множестве операциями и предикатами.
4. Нет правильного ответа.
Алгебраическая система называется конечной, если:
+1. Конечно множество А.
2. Множество А пустое.
3. Множество А не пустое.
4. Нет правильного ответа.
Алгебраическая система называетсяА; ΩF,ΩPалгеброй, если:
+1.
ΩP
=
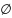и ΩF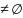
.
2. ΩP и ΩF .
3.
ΩP
и ΩF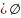
.
4. Нет правильного ответа.
Алгебраическая система называетсяА; ΩF,ΩP моделью, если:
1.
ΩP=
иΩF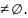
2. ΩP и ΩF .
+3. ΩP и ΩF .
4. Нет правильного ответа.
Продолжите : «Алгебра- это…..»
1. Учебник.
2. Пустое множество.
+3. Непустое множество А, на котором задана совокупность операций, переводящих элементы из А в А.
4. Нет правильного ответа.
Подмножество В множества А называется замкнутым относительно операции Fi,если
1. Fi переводит элементы из А в В.
+2. Fi переводит элементы из В в это же В.
+3. Fi переводит элементы из А в это же А.
4. Нет правильного ответа.
Если подмножество В (В
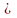А)
замкнуто относительно всех операции
алгебры, то В=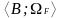
называют
+1.
Подалгеброй алгебры
.
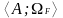2. Подмножество В.
3. Подмножество А.
4. Нет правильного ответа.
Всякое отображение основного множества А в (на) основное множество В называем
1. Изоморфизмом алгебры.
2. Гомоморфизмом алгебры.
3. Авоморфизмом.
+4. Отображением алгебры А в (на) алгебру В.
Взаимно однозначное (биективное) отображение множества А в(на) В, сохраняющее главные операции алгебры т.е. для которого выполняются соотношения:
(Fi(x1,x2,…,xn))
= Gi(
(x1),…,
(xmi))
для всех i,
1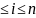
,
и
для любогоx1,x2,…xmi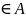
называется:
+1. Изоморфизмом алгебры А=А;F1, F2, …, Fn в(на) однотипную алгебру
В=B; G1, G2, …, Gn.
2. Гомоморфизмом алгебрыА=А;F1, F2, …, Fn в(на) однотипную алгебру
В=B; G1, G2, …, Gn.
3. Авоморфизмом.
4.Отображением алгебры А в (на) алгебру В.
Изоморфизм алгебры на себя называется:
+1. Автоморфизмом.
2. Гомоморфизмом А=А;F1, F2, …, Fn в(на) однотипную алгебру
В=B; G1, G2, …, Gn.
3. Отображение алгебры.
4. Нет правильного ответа.
Отображение множества А в (на) множество В, сохраняющее главные операции алгебры, т.е. для которого выполняются соотношения:
(Fi(x1,x2,…,xn)) = Gi( (x1),…, (xmi)) для всех i, 1 , и для любогоx1,x2,…xmi называется:
1. Изоморфизмом алгебры А=А;F1, F2, …, Fn в (на) однотипную алгебру
В=B; G1, G2, …, Gn.
+2. Гомоморфизмом алгебры А=А;F1, F2, …, Fn в (на) однотипную алгебру
В=B; G1, G2, …, Gn;
3. Авоморфизмом.
4. Отображением алгебры А в (на) алгебру В.
Множество с одной двуместной операцией называют :
+1.Группоид.
2.Полугруппа.
3.Моноид.
4.Группа.
Группоид, в котором операция ассоциативная называется:
1. Группоид.
+2. Полугруппа.
3. Моноид.
4. руппа.
Полугруппа с единицей называется:
1. Группоид.
2. Полугруппа.
+3. Моноид.
4. Группа.
Моноид, в котором для любого элемента существует обратный элемент, называется:
+1. Группой.
2. Группоид.
3. Полугрппа.
4. Кольцо.
Множество G с одной бинарной операцией «»называем группой, если:
1. Операция ассоциативна.
2. Существует единица в G.
3. Для любого элемента a Gсуществует обратный элемент.
+4. Выполняются все сразу.
Если операция в группе называется умножением, то группа называется
+1. Мультипликативной
2. Аддитивной.
3. Коммутативной.
4. Абелевой.
Группа называется абелевой или коммутативной, если
+1.
Для
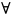a,b
G:
a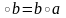
.
2. Для a,b G: a .
3.
Для
a,b
G:
a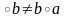
.
4. Нет правильного ответа.
Подгруппа циклической группы является
+1. Циклической.
2. Образующей.
3. Аддитивной.
4. Абелевой.
Непустое множество R, на котором введены две бинарные операции сложение и умножение называется
+1.Кольцом;
2.Областью целочисленности.
3.Полем.
4.Нет правильного ответа.
Кольцо называется коммутативной, если:
+1. Для a,b R: a .
2. Для a,b R: a .
3. Для a,b R: a .
4. Нет правильного ответа.
Аддитивную единицу обозначают через:
1. 1.
+2.
0 или
.
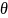3. +.
4. Нет правильного ответа.
Коммутативное кольцо без делителей нуля, отличных от тривиального делителя нуля, называют:
+1. Целочисленным кольцом.
2. Полем.
3. Коммутативное кольцо.
4. Нет правильного ответа.
Если в кольце Rсуществует единица относительно умножения, то эту мультипликативную единицу обозначают через
1. 0.
+2. 1.
3. +.
4. ⃘.
Наименьшее натуральное число k такое, что а+а+…а=0 для всех a R называют
+1. Характеристикой кольца R.
2. Нулевое кольцо.
3. Минимум кольца.
4. Нет правильного ответа.
Аддитивная единица, т.е. 0, не имеет
+1. Мультипликативного обратного.
2. Мультипликативной единицы.
3. Мультипликативного нуля.
4. Нет правильного ответа.
Элементы 0 и 1 являются различными элементами
+1. Ненулевого кольца R.
2. Пустого кольца R.
3. Единичного кольца R.
4. Нет правильного ответа.
Множество всех комплексных чисел обозначается через
1. Q.
2. R.
3. Z.
+4. C
Коммутативное кольцо, у которого ненулевые элементы образуют коммутативную группу относительно умножения, называют:
1. Кольцом.
+2. Полем.
3. Решеткой.
4. Матроидом.
Поле вещественных чисел обозначается через:
+1. R;+, .
2. Q;+, .
3. C;+, .
4. Z;+, .
Поле рациональных чисел обозначается через
1. R;+, .
+2. Q;+, .
3. C;+, .
4. Z;+, .
Поле комплексных чисел обозначается через
1.R;+, .
2.Q;+, .
+3. C;+, .
4.Z;+, .
Если а 0, то в поле единственным образом разрешимо уравнение
+1.
а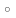
х=b.
2. а х=0.
3. а х=1.
4. Нет правильного ответа.
Множество М с двумя бинарными операциями
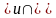называется
+1. Решеткой.
2. Кольцом.
3. Группой.
4. Матроидом.
Если в решетке
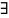0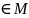
,
что для
а:
0
а=0,
то 0 называется
+1. Нулем или нижней гранью решетки.
2. Единицей или верхней гранью решетки.
3. Нулем или верхней гранью решетки.
4.Единицей или нижней гранью решетки.
Если в решетке
,
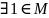что для
а:
1
а=1,
то 1 называется
1. Нулем или нижней гранью решетки.
+2. Единицей или верхней гранью решетки.
3. Нулем или верхней гранью решетки.
4. Единицей или нижней гранью решетки.
Если нижняя (верхняя) грань существует, то она
+1. Единственна.
2. Разрешима.
3. Двойственна.
4. Нет правильного ответа.
В ограниченной дистрибутивной решетке с дополнением выполняется:
1. Дополнение а’ единственно.
2. Дополнение иволютивно:а”=а.
3. Грани дополняют друг друга:1’=0, 0’=1.
+4. Все перечисленное;
Дистрибутивная ограниченная решетка, в которой для каждого элемента существует дополнение, называется
+1. Булевой алгеброй;
2. Решеткой.
3. Кольцом.
4. Группой.
По теореме о свойствах дополнения а’’=…
1. 1.
+2. а.
3.0.
4.а’.
Какие свойства следуют из свойств ограниченности решетки:
1. A 1= 1.
2. А 0 = 0.
3.А 0 = А.
+4. Только 1. И 2.
По теореме о свойствах дополнения (А В)’=…
1. A 1= 1.
2. А’ В’.
+3. А’ В’.
4. Все перечисленное.
А А’=…
+ 1. 1.
2. 0.
3. А’.
4. А
Конечное множество Е, Е=n, и его семейство подмножеств Х, Х 2Еназывается
1. Булеаном.
+2. Матроидом.
3. Решеткой.
4. Группой.
Элементы множества Х называют
1.Зависимыми множествами.
+2.Независимыми множествами.
3.Пустым множеством.
4.Свободным матроидом.
Элементы из 2Еназывают
1.Зависимыми множествами.
+2.Независимыми множествами.
3.Пустым множеством.
4.Свободным матроидом.
График одноаргументной функции у=f(x) (x A, y А) является
1.
Подмножеством декартового произведения
А
А
А,
т.е.f=А
А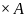
.
+2. Подмножеством декартового произведения А А, т.е.f=А А.
3. Независимым.
4. Нет верных ответов.
График двухаргументной функции у=f(x1,х2) (x1 A,x2 A,y А) является
+1. Подмножеством декартового произведения А А А, т.е.f=А А .
2. Подмножеством декартового произведения А А, т.е.f=А А.
3. Независимым.
4. Нет верных ответов.