§19. Приложения теории булевых функции к анализу и синтезу контактных схем.

215. Под контактной (переключательной) схемой понимается схема, состоящая из

1. Замкнутых и разомкнутых контактов, соединенных параллельно или последовательно, или смешанным образом;

2. Замкнутых и разомкнутых контактов.

3. Замкнутых и разомкнутых контактов, соединенных параллельно или последовательно.

4. Нет правильных ответов.

216. Контакты (переключатели) можно рассматривать как

1. Булевы переменные;

2. Монотонные переменные.

3. Самодвойственные переменные.

4. Линейные функции.

217. Отрицанием контакта х называется контакт, равный 1, если х=

1. 1.

2. 0;

3. 2.

4. 3.

218. Если контакт разомкнут, то полагаем х=

1. 0;

2. 1.

3. 2.

4. 3.

219. Если контакт замкнут, то полагаем х=

1. 0.

2. 1;

3. 2.

4. 3.

§20. Приложение теории булевых функции к анализу и синтезу схем их функциональных элементов.

220. Устройство, реализующее отрицание показано на рисунке

1. 1; В. 2. С. 3. D. 4.

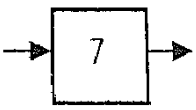
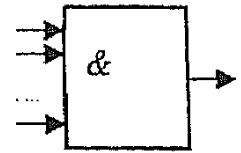
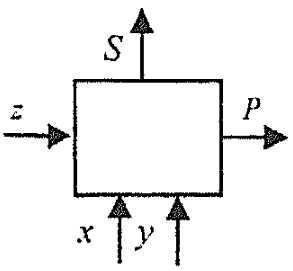
221. Устройство, реализующее конъюнкцию показано на рисунке

А. 1. В. 2; С. 3. D. 4.

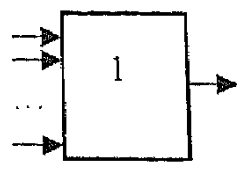
222. Устройство, реализующее дизъюнкцию показано на рисунке

А. 1. В. 2. С. 3; D. 4.

223. Сложность схем из функциональных элементов – это

А. Число функциональных элементов в этой схеме;

2. Число входов устройства.

3. Число выходов устройства.

4. Число решений функции.

§21. Функциональная декомпозиция.

224. Если декомпозиция выполняется при условии, что Xⁱ 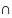X^j= для любых i, j,i j, то декомпозиция называется

1. Разделительной;

2. Неразделительной.

3. Двумерной разделительной декомпозицией.

4. Нет правильных ответов.

225. Если хотя бы одно пересечение подмножеств Xⁱ и X^j не пусто, то декомпозиция называется

1. Разделительной.

2. Неразделительной;

3. Двумерной разделительной декомпозицией.

4. Нет правильных ответов.

226. Если булева функция f(X) допускает декомпозицию при к=1 и m=1т.е. f(X)=g0(X⁰,g₁(X¹)), то такая декомпозиция называется

1. Простой;

2. Сложной.

3. Разделительной.

4. Неразделительной.

227. Булева функция f(X), зависящая от н переменных, допускает двумерную разделительную декомпозицию кратности один тогда и только тогда, когда

1. Декомпозиционная матрица, соответствующая заданному разбиению множества Х на непересекающиеся подмножества Х⁰ и Х¹, содержит не более двух различных столбцов значений функции;

2. Декомпозиционная матрица, соответствующая заданному разбиению множества Х на непересекающиеся подмножества Х⁰ и Х¹, не содержит значений функции.

3. Декомпозиционная матрица, соответствующая заданному разбиению множества Х на непересекающиеся подмножества Х⁰ и Х¹, содержит не более трех различных столбцов значений функции.

4. Декомпозиционная матрица, соответствующая заданному разбиению множества Х на непересекающиеся подмножества Х⁰ и Х¹, содержит не одного двух различных столбцов значений функции.

228. Булева функция f(X), зависящая от н переменных, допускает двумерную разделительную декомпозицию кратности k тогда и только тогда, когда

1. Декомпозиционная матрица функции f(X), соответствующая заданному разбиению множества Х на непересекающиеся подмножества Х⁰ и Х¹, содержит не более 2^k различных столбцов;

2. Декомпозиционная матрица функции f(X), соответствующая заданному разбиению множества Х на непересекающиеся подмножества Х⁰ и Х¹, содержит не более 2^{k -1} различных столбцов.

3. Декомпозиционная матрица функции f(X), соответствующая заданному разбиению множества Х на непересекающиеся подмножества Х⁰ и Х¹, содержит не более 2^k+1 различных столбцов.

4. Декомпозиционная матрица, соответствующая заданному разбиению множества Х на непересекающиеся подмножества Х⁰ и Х¹, содержит не более двух различных столбцов значений функции.