Тухбатуллина Диляра гр.4109

Глава 1. Множества, отношения и функции.

1. Выберите правильное значение слова множество?

1. Это условие, выраженное в форме логического утверждения.

2. Это процедура, которая, будучи запущенной, порождает некоторые объекты по заданным правилам.

3. Фундаментальное неопределяемое понятие.

+4. Собрание определенных и различных между собой объектов, мыслимых как единое целое.

2. Продолжите: Предикат - это…?

1. Это процедура, которая, будучи запущенной, порождает некоторые объекты по заданным правилам.

2. Объединение в одно целое объекты, хорошо различимые нашей интуицией или мыслью.

+3. Это некоторое условие, выраженное в форме логического утверждения.

4. Фундаментальное неопределяемое понятие.

3. Что такое порождающая процедура?

+1. Которая, будучи запущенной, порождает некоторые объекту по заданному правилу.

2. Которая, будучи запущенной, выявляет принадлежность объекта данному множеству.

3. Которая, будучи запущенной, определяет все элементы данного множества.

4. Которая, будучи запущенной, определяет истинность высказывания.

4. С помощью чего можно задать множество:

1. Перечислением элементов.

2. Предикатом.

3. Порождающей процедурой.

+4. Всеми перечисленными

5. Выберите правильную формулировку аксиомы пары?

1. Если множества A и B составлены из одних и тех же элементов, то они совпадают.

2. Существует такое множество, что ни один элемент x ему не принадлежит.

3. Для каждого семейства множеств R существует множество S, состоящее из тех и только тех элементов, которые принадлежат некоторому множеству А из R.

+4. Для произвольных а и b существует множество, единственными элементами которого являются а и b.

6. Объединением множеств А и В называют множество С:

1. Каждый элемент которого является элементами А и В.

+2. Каждый элемент которого является элементами А или В.

3. Каждый элемент которого есть элемента А, но не В.

4. Каждый элемент которого есть элемент В, но не А.

7. Что называется пересечением множеств А и В называется множество С:

1. Каждый элемент которого является элементами А или В.

+2. Каждый элемент которого является элементами как и А, так и В.

3. Каждый элемент которого есть элемент в, но не а.

4. Каждый элемент которого есть элемент А, но не В.

8. Разностью множеств А и В называется множество С:

1. Элементы которого принадлежат каждому из множеств А и В.

+2. Состоящее из элементов множества А, не принадлежащих множеству В.

3. Элементы которого принадлежат хотя бы одному из множеств А и В.

4. Элементы которого принадлежат в точности одному из множеств А или В.

9. Какая формула соответствует дистрибутивному закону:

1. A  B = B  A.

2. A  (A  B) = A.

3. A  (B  C) = (A  B)  C.

+4. A  (B С) = (A  B)  (A  C).

10. Ассоциативный закон записывается в виде:

1. A  B = B  A.

2. A  (B С) = (A  B)  (A  C).

3. A  (A  B) = A.

+4. A  (B  C) = (A  B)  C.

11. Коммутативный закон записывается в виде:

+1. A  B = B  A.

2. A  (B С) = (A  B)  (A  C).

3. A  (A  B) = A.

4. A  (B  C) = (A  B)  C.

12. Закон поглощения записывается в виде:

1. A  B = B  A.

2. A  (B С) = (A  B)  (A  C).

+3. A  (A  B) = A.

4. A  (B  C) = (A  B)  C.

13. Закон де Моргана записывается в виде:

1. A  B = B  A.

2. A  (B С) = (A  B)  (A  C).

3. A  (A  B) = A.

+4. A  B = A  B.

14. Идемпотентность записывается в виде:

1. A  B = B  A.

2. A  (B С) = (A  B)  (A  C).

+3. A  A = A.

4. A  B = A  B.

15. Семейство подмножеств {B₁,B₂,…,B_n}, образует разбиение множества А тогда и только тогда, когда:

1. B_i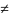 , 1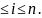

2. B_iB_j=, если i j.

3. B₁B₂…B_n=A.

+4. Все перечисленное.

16. Упорядоченной парой называется:

+1. Объект (а,b) такой, что (а,b)=(с,d) тогда и только тогда, когда а=с и b=d;

2. Множество упорядоченных пар (а,b), таких, что аA и bB.

3. Подмножество R декартового произведения А В.

4. Это упорядоченный набор элементов.

17. В упорядоченной паре (а,b) элементы считаются:

+1. a – первый элемент, b – второй;

2. a =1, b=0.

3. a - второй элемент, b – первый.

4. a=0, b=1.

18. Декартовым произведением двух множеств А и В называется множество:

1. Упорядоченных пар (а,b) такой, что (а,b)=(с,d) тогда и только тогда, когда а=с и b=d.

+2. Упорядоченных пар (а,b), таких, что а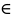 А и b B.

3. Упорядоченных пар (а,b), таких, что а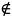 А и b B.