• Обобщенная статическая характеристика описывается

• Линеаризованным выражением ,

• трение и масса золотника пренебрежимо малы ,

• параметры жидкости постоянны .

Представленные допущения вполне обоснованы. Действительно, обобщенная статическая характеристика ГУ сопло - заслонка практически линейна в широком диапазоне смещений заслонки (см. выше), трение в золотниках обычно не превышает 10Н и существенно меньше сил давления, действующих на золотник, а масса золотников в ЗГР небольшой и средней мощности составляет 0,005…0,015 кг.

Исходные дифференциальные уравнения движения ГУ включают по аналогии с ДГП уравнение сил и уравнение расходов.

Уравнение сил : р_д А_з = С_з Х , А_з =  d_з² / 4 – площадь торца золотника , d_з – диаметр золотника , С_з – суммарная жесткость пружин под торцами золотника, Х – смещение золотника от среднего положения .

Уравнение расходов: k_Qhh – k_Qp р_д=А_з(dХ/dt)+(V_z/2E ) (dp_д /dt) .

Здесь V_z - объем сжимаемой жидкости под одним торцем золотника (обычно не превышает 1…2см³).

В уравнение расходов, в отличие от жесткой модели ДГП, не входит член с перетечками жидкости, поскольку в диагонали моста сопло - заслонка они практически отсутствуют.

В результате совместного решения обоих уравнений после приведения к операторной форме записи получим выражение передаточной функции ГУ :

p_д (s) k_ph x (s) k_xh

W_гу (s) =  =  или W_гу (s) =  =  ,

h (s) Т_гу s + 1 h (s) Т_гу s + 1

где Т_гу = (1/k_Qp ) [ ( A_з² / C_з ) + (V_z / 2E ) ] – постоянная времени ГУ , k_xh= k_ph A_з / C_з – коэффициент передачи ГУ.

Из представленных выражений следует , что для увеличения быстродействия ГУ сопло – заслонка (уменьшения Т_гу ) следует повышать k_Qp , т.е. расход жидкости через сопла(k _Qp= k_Qh / k_ph= Q_c / h₀ k_ph) , уменьшать d_з и увеличивать жесткость пружин С_з . Последнее обуславливает необходимость применения золотников с малым рабочим ходом , т.е. длина окна не должна превышать 0,5…1 мм .

Наиболее эффективно уменьшение диаметра золотника. Так, уменьшение d_з в 2 раза снижает Т_гу (при прочих равных условиях) в 16 раз. Поэтому в ГУ небольшой и средней мощности обычно используют золотники с диаметром не более 5…8мм.

Второй член в квадратных скобках выражения для Т_гу практически не влияет из -за малости объема V_z .

Из полученной передаточной функции следует, что при ступенчатом перемещении заслонки процесс нарастания давления p_д и, следовательно, перемещения Х имеет затянутый апериодический характер, что иллюстрируется рис.59. Там же представлена структурная динамическая схема ГУ.

k_xh



T_гу s + 1

h (s) x (s)

Рис.59

Существующие конструкции ГУ этого типа для приводов небольшой и средней мощности имеют величину Т_гу не менее (8 10^-3 )с при диаметре золотника 5…6мм, и (15 10^-3 )с для диаметра 8мм.

Полученные выше дифференциальные уравнения движения ЭМП и ГУ не отражают такой важный фактор, как силовую реакцию струй жидкости, вытекающей из сопел заслонку. Данная реакция воздействует на заслонку и , следовательно , якорь ЭМП , нагружая его. Это воздействие ( в виде обратной связи ) обуславливает необходимость рассмотрения ЭМП и ГУ как общую динамическую систему – ЭГУ .

Физическая картина формирования реакции струй поясняется рис.60. На заслонку ГУ воздействует 2 силы - гидростатическая и гидродинамическая. Первая создается давлением р3 перед соплом и дросселирующим зазором (оно принимается одинаковым). Вследствие абсолютной малости зазора z между срезом сопла и заслонкой, не превышающего 10% диаметра сопла, давление в зазоре практически не падает и полностью давит на заслонку на площади А_с = π d_c²/4, образуя гидростатическую составляющую : R₁= p₃ A_c . Эта же составляющая у правого сопла равна R₂= p₄ A_c и направлена встречно.

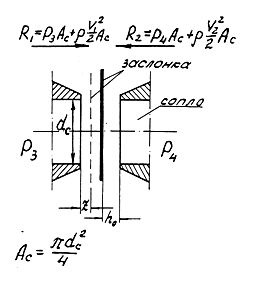
Рис.60

С другой стороны, струя жидкости, вытекающая из сопла с большой скоростью (50м/с и выше), создает динамическое давление в результате торможения у заслонки и разворота потока. При этом гасится практически весь скоростной напор и кинетическая энергия струи переходит в потенциальную энергию давления, создавая гидродинамическую составляющую реакции струй : R₃ = A_c (ρ V₁² / 2) , где ρ - плотность жидкости, V₁ – cреднее значение скорости потока в левом сопле

(V₁= Q₁/A_c, Q₁ - расход жидкости через левое сопло).

По аналогии гидродинамическая составляющая от правого сопла равна R₄ = A_c (ρ Q₂²/ A_c²) и вычитается из R₃.

Результирующая силовая реакция определится выражением

R = (R₁+R₃) - (R₂+R₄) = A_c (p₃ - p₄) + ρ/A_c (Q₁² - Q₂²).

После ряда преобразований можно записать:

R = A_c ( k₁ p_д + k₂ h ) .

Здесь k₁ и k₂ – конструктивные коэффициенты .

Тогда уравнения системы ЭМП – ГУ примут вид :

1)Уравнение сил на якоре ЭМП в операторной форме записи :

С_эмп(Т_эмп² s²+2_эмпТ_эмп s+1)h(s) = k_Fi i_y(s) - A_c[k₁ p_д (s) + k₂ h (s)] ,

2) Уравнения ГУ сопло – заслонка :

k_ph h (s) = ( Т_гу s + 1 ) p_д (s) , Х(s) = (A_з /C_з ) p_д (s) .

Поскольку быстродействие ЭМП очень велико , на практике можно считать Т_эмп = 0 . Тогда структурно – динамическая схема ЭГУ на основании записанных уравнений примет вид рис.61: :

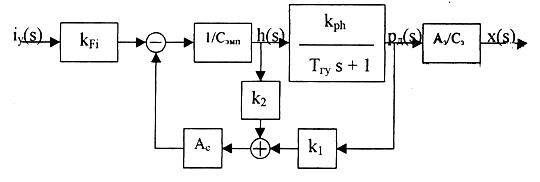Рис.61

В результате преобразований данной схемы или совместного решения записанных уравнений получим передаточную функцию

ЭГУ – 1(под этим индексом понимается схема ЭГУ , включающая золотник с пружинами) относительно тока i_y :

Х(s) k_эгу

W_эгу (s) =  =  ,

i_y (s) Т_эгу s + 1

здесь k_эгу = k_Fi k_ph A_з / C_эмп С_з ( 1 + С_зс С_эмп ) – коэффициент передачи ЭГУ , С_зс = А_с (k₂ + k₁ k_ph ) – жесткость реакции струй,

Т_эгу= Т_гу (1+ k₂A_c /С_эмп) / (1 + C_зс / C_эмп ) – постоянная времени ЭГУ . Т_эгу < T_гу .

Отсюда следует, что реакция струй уменьшает коэффициент передачи системы ЭМП – ГУ в раздельном представлении, а также повышает быстродействие .

Существующие конструкции ЭГУ – 1 с золотниками малого диаметра (5…6мм) и Х_m=0,5…1мм имеют по статистическим данным постоянную времени Т_эгу=(5…6) 10^-3с, что близко к теоретическому пределу.

Полная структурно – динамическая схема ЭГУ-1 в линейном приближении с учетом электрической цепи ЭМП показана на рис.62.

В соответствии с ней ЭГУ – 1 описывается передаточной функцией 5-го порядка по отношению к напряжению U_y .

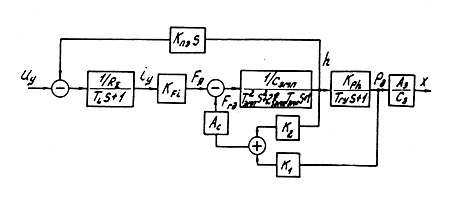
Рис.62

Схема ЭГУ – 1 получила широкое распространение в авиационных следящих гидроприводах различного назначения, она технологически отработана, относительно проста в производстве, надежна. Вместе с тем ей присущ ряд недостатков :

• Увеличенное трение золотника ЗГР , обусловленное радиальной составляющей силы сжатия пружин, обладающих высокой жесткостью.

Пружины имеют предварительное поджатие, превышающее величину Х_m и при жесткости каждой из них 150…200Н/мм создают значительное усилие как в осевом, так и частично в радиальном направлении. Это приводит к прижатию золотника к внутренней поверхности гильзы и появлению повышенного трения. Поэтому в конструкции ЗГР предусмотрены меры разгрузки , когда пружины опираются не напрямую в торец золотника, а через специальные промежуточные детали. Существуют схемы разгрузки на шариках, на конусах и на иглах (рис.63). Разгрузка на шариках (а) наиболее проста, но наименее эффективна. В настоящее время наиболее широко используется разгрузка на конусах (б), но самой лучшей считается разгрузка на иглах (в) вследствие минимальной базы действия радиальных сил.

Недостатком этой разгрузки является сложность реализации в золотниках малого диаметра (менее 8мм).

Несмотря на наличие разгрузки, сила трения в золотнике ЭГУ – 1 может достигать 10…15Н.

• Сравнительно низкая температурная стабильность статических и динамических характеристик.

Это объясняется тем, что коэффициент передачи ЭГУ и постоянная времени зависят от гидравлических параметров (коэффициентов k₁ и k₂), которые сильно меняются по температуре из – за вязкости жидкости. Наклон характеристики давления ГУ сопло – заслонка может различаться в 1,5…2 раза в диапазоне температур (– 60⁰С …+100⁰С), что отрицательно влияет на качество следящего гидропривода в целом.

• В ряде случаев недостаточное быстродействие.

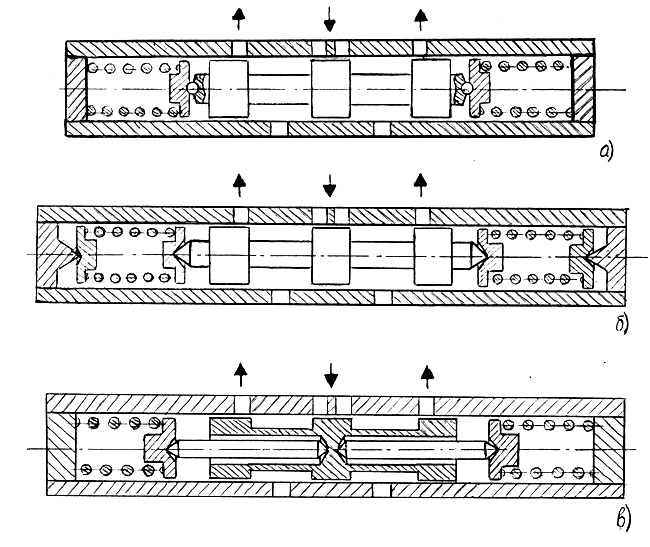
Рис.63

В следящих гидроприводах высокого быстродействия (например, рулевых приводах маневренных самолетов и ракет) величина постоянной времени 5…6 миллисекунд уже оказывает существенное влияние на характеристики контура и нуждается в уменьшении. В рамках рассмотренной схемы ЭГУ – 1 снизить Т_эгу практически не удается, поэтому с середины 60-х г.г. проводились масштабные ОКР по разработке альтернативных схемных решений для перспективных ЭГУ.

Рассмотрим схемы и характеристики ЭГУ других типов, не имеющих отмеченных выше недостатков ЭГУ – 1. Это схемы с различными видами обратных связей по положению золотника. Их коренное отличие – использование т.н. «свободноплавающего золотника» без силовых пружин, обладающего низким уровнем трения – 3…4Н и менее.

Наиболее распространенным вариантом такого ЭГУ, широко используемым в настоящее время в авиационных и ракетных ЭГСП является ЭГУ с упругой механической обратной связью по положению золотника (условное обозначение – ЭГУ – 2). Его схема представлена на рис.64. Особенность схемы – наличие упругой пластины (пружины обратной связи), соединяющей золотник с заслонкой.

Рис.64

Принцип работы ЭГУ – 2 основан на балансе силы , создаваемой ЭМП на заслонке при протекании тока i_y в обмотках , и силы деформации пружины обратной связи , связанной со свободноплавающим золотником . ЭГУ в нормальных условиях работает при минимальном перепаде давления р_д , близком к 0 и обусловленном низким уровнем трения свободноплавающего золотника.

В основе ЭГУ – 2 также находится гидравлический мост сопло – заслонка со всеми необходимыми элементами. При подаче тока i_y в обмотки ЭМП якорь – заслонка смещается, например, влево. Давление р₃ увеличивается, р₄ - уменьшается, под действием перепада р_д = (р₃ – р₄ ) золотник смещается вправо, сгибая пружину обратной связи и тем самым стремясь вернуть заслонку в исходное нейтральное положение. Когда усилие, создаваемое ЭМП на заслонке уравновесит силу деформации пружины, заслонка придет практически в нейтральное положение и движущая сила для золотника (перепад р_д) прекратится. Золотник остановится в смещенном положении и нагружен только небольшой силой изгиба пружины обратной связи.

При изменении тока управления баланс сил нарушится и вызовет перемещение золотника в новое положение. Таким образом, золотник отслеживает величину тока i_y c некоторым коэффициентом пропорциональности.

Лекция 15.

Рассмотрим уравнения движения для ЭГУ - 2 и его динамические свойства с точки зрения сравнения с ЭГУ - 1.

С учетом ранее принятого допущения Т_эмп = 0 и р_д = 0 уравнение баланса сил на якоре ЭМП примет вид :

k_Fi i_y (s) = C_эмп h (s) + C_oc [Х(s) + h(s)] +k₂ A_c h(s) .

Здесь отсутствует гидростатическая составляющая силовой реакции струй. Но добавился новый член, учитывающий силу изгиба пружины обратной связи, равный ее жесткости С_ос, умноженной на величину деформации. Последняя определяется суммой координат Х и h, поскольку перемещение золотника и заслонки осуществляется в противоположных направлениях.

Уравнение расходов ГУ сопло – заслонка :

k_Qh h(s) = A_з s Х(s) .

В отличие от ЭГУ - 1 мост сопло - заслонка не нагружен давлением р_д , поэтому в уравнении обобщенной статической характеристики ГУ (левая часть уравнения расходов) отсутствует член с давлением р_д . По этой же причине в правой части уравнения нет составляющей расхода на сжимаемость.

В результате решения уравнений можно записать выражение передаточной функции ЭГУ :

Х(s) k_эгу

W_эгу (s) =  =  ,

i_y(s) Т_эгу s + 1

где k_эгу = k_Fi / C_oc – коэффициент передачи ЭГУ ,

Т_эгу = (А_з / k_Qh )(C_ / C_oc)– постоянная времени . Добротность замкнутого контура ЭГУ равна 1/Т_эгу . Здесь С_ = С_эмп + k₂ A_c + C_oc .

Из выражения для k_эгу следует, что он не зависит от гидравлических параметров, а следовательно отсутствует сильное влияние температуры жидкости. Стабильность коэффициента k_Fi зависит от постоянства свойств магнитов поляризации, индукция которых несколько уменьшается с ростом температуры вплоть до точки Кюри. С другой стороны, жесткость металла пружины обратной связи также снижается по температуре. Поэтому данная схема ЭГУ характеризуется очень высокой температурной стабильностью коэффициента передачи. Она широко используется в ЭГСП, работающих в условиях как высоких, так и низких температур рабочей жидкости и окружающей среды ( - 60⁰С…+400⁰С).

Постоянная времени может быть уменьшена за счет повышения добротности ЭГУ - 2. Способы ее увеличения :

• применение золотников малого диаметра , как и в схеме ЭГУ - 1, но эффективность данной меры существенно ниже (при уменьшении диаметра золотника в 2 раза постоянная времени снижается только в 4 раза),

• увеличение расхода через сопла Q_c , но ценой возрастания энергетических потерь в ГУ,

• увеличение жесткости пружины обратной связи , т.е. в конечном счете использование ЭМП с повышенными тяговыми свойствами . Это может быть достигнуто за счет применения мощных магнитов поляризации на редкоземельной основе и увеличения размеров магнитопроводов и якоря с целью повышения тока насыщения , или изготовления этих деталей из кобальтовых сплавов или магнитных материалов типа «металлическое стекло», имеющих высокую индукцию насыщения.

• уменьшение жесткости подвески якоря С_эмп . Однако при этом увеличивается механическая постоянная времени ЭМП, что отрицательно сказывается на быстродействии ЭГУ в целом.

Практика показала, что на существующей элементной базе обеспечить добротность более 200 1/c (что соответствует Т_эгу = 5 10^-3 с) в рамках данной схемы как правило не удается .

Полная структурно – динамическая схема линеаризованного ЭГУ – 2 с учетом электрической цепи ЭМП соответствует системе 5-го порядка . Она представлена на рис.65.

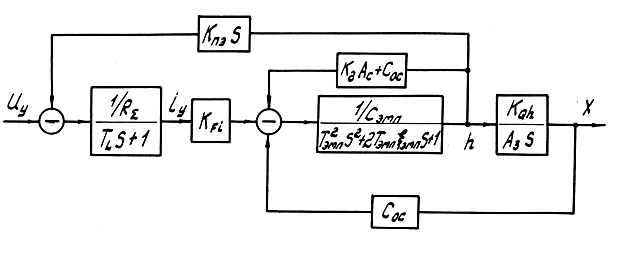
Рис.65

В целом быстродействие ЭГУ – 2 выше , чем ЭГУ – 1 . Постоянная времени Т_эгу для ЭГУ - 2 по расчетам  в 1,5 раза ниже при одинаковых параметрах ЭМП и ГУ сопло – заслонка . Это иллюстрируется сравнительными логарифмическими частотными характеристиками ЭГУ – 1 и ЭГУ – 2, показанными на рис.66. Характеристики приведены к единичному коэффициенту передачи и рассчитаны на основании структуры на рис.65.

Рассмотрим еще одну схему ЭГУ с обратной связью по положению золотника, получившую широкое распространение в современных ЭГСП, применяющихся в ЭДСУ сверхзвуковых аэродинамически неустойчивых самолетов. Это схема ЭГУ с электрической обратной связью по положению золотника, условно обозначаемая как ЭГУ – 3 .

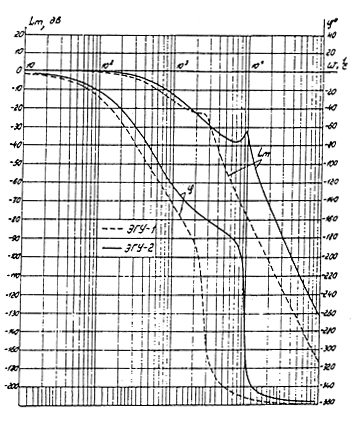
Рис.66

Радикально увеличить добротность ( следовательно , повысить быстродействие и точность работы ЭГУ) можно включением электрического усилителя в следящий контур управления золотником , используя электрическую обратную связь по положению золотника . Схема ЭГУ - 3 дана на рис. 67.

Помимо высокого быстродействия ЭГУ – 3 характеризуется минимальной зоной нечувствительности , точным позиционированием золотника (повышенной линейностью управляющей характеристики) , оперативным изменением коэффициента передачи и смещения нуля .

По аналогии с предыдущими разделами рассмотрим уравнения движения и особенности динамики ЭГУ - 3.

Исходные уравнения :

Электрический усилитель сигнала ошибки : U_ = U_вх - U_oc ,

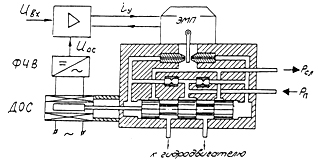
Рис.67

U_y = k_y U_ , здесь U_θ - напряжение сигнала ошибки,

k_y - коэффициент усиления по напряжению.

Электромеханический преобразователь :

Электрическая цепь U_y = (R_o+R_вых) + L (di_y/dt) + k_пэ (dh/dt) ,

Механическая система m_я (d²h/dt²) = k_Fi i_y – b_я (dh/dt) – C_эмп h - k₂ A_c h ,

Гидроусилитель сопло - заслонка k_Qh h = A_з dХ/dt ,

Индукционный датчик обратной связи T_oc dU_oc/dt + U_oc = k_ocХ.

Здесь Т_ос - постоянная времени цепи обратной связи .

В этих уравнениях также не учитывается гидростатическая составляющая

реакции струй и перепад давления р_д .

Cтруктурно – динамическая схема линеаризованного ЭГУ – 3 на основании данных уравнений, записанных в операторной форме имеет вид :

1/R_



T_Ls+1

k_hi^



T_эмп^{ 2}s²+2T_эмп^_эмп^s+1

k_Qh

_

A_з s

U

k_y

k_пэs

_вх U_y i_y h Х

- -

k_oc

_

T_ocs+1

U_oc

Упрощенная структурная схема данного ЭГУ (Т_эмп^=0 ,Т_ос=0), приведенная к единичной обратной связи :

К_д



s(T_L^s+1)

Х_вх Х

-

Здесь Х_вх = U_вх / k_oc , K_д = k_y k_hi^ k_Qh k_oc / R_ A_з – добротность замкнутого контура ЭГУ – 3 , T_L^ = T_L + ( k_hi^ k_пэ / R_ ) – электрическая постоянная времени с учетом противоЭДС.

Тогда передаточная функция замкнутого контура :

Х(s) k_эгу

W_эгу (s) =  =  ,

U_вх(s) Т_эгу² s² + 2 T_эгу _эгу s + 1

где k_эгу = 1/ k_oc – коэффициент передачи ЭГУ – 3 , Т_эгу = (Т_L^/K_д )^0.5 – постоянная времени , _эгу = 1/ 2 ( T_L^ k_д )^0.5 – коэффициент относительного демпфирования .