
Санкт-Петербургский государственный политехнический университет
Кафедра
конструкторско-технологических инноваций
Отчёт
о лабораторной работе
Дисциплина: Вычислительная математика
Тема: Решение плоской задачи теории упругости методом конечных элементов
Студент гр. 20411.1 Мячина Л.А.
Преподаватель Петров И.П.
“ “ 2013 г.
Санкт-Петербург
2013
Задание
Решить плоскую задачу теории упругости для заданной детали (вариант №9), размеры которой и схема нагружения представлены на рис.1, размеры детали представлены в миллиметрах.:
О
Рис.1. Заданная деталь
Решить систему двух дифференциальных уравнений в частных производных, решением которой будут функции горизонтальных w(x,y) и вертикальных v(x,y) перемещений:
 ,
,
исходя из заданных граничных условий;
Граничные условия: приложенная нагрузка – сосредоточенные горизонтальные силы 1200Н и -1200Н;
Толщина детали принимается равной 1;
Модуль упругости принимается равный 2∙1011Па;
Коэффициент Пуассона равен 0,25;
Построить график зависимости координат х узлов в сечении ОХ от горизонтальных перемещений U при разных величинах разбиения для демонстрации зависимости точности решения от величины разбиения на участке от 0 до 40 мм.
Теоретические сведения
При решении задач механики сплошных сред методом конечных элементов двумерная область, в которой ищется решение, заменяется дискретной моделью. Эта модель строится из многоугольников (треугольников или четырехугольников), называемых конечными элементами и объединенных в узлах.
Сетка конечных элементов считается заданной, если определены номера элементов и узлов, и их координаты. Данные о сетке элементов требуют подготовки большого объема информации. Неверно заданная информация об элементах является одним из основных источников ошибок при решении задач методом конечных элементов. Устранить эти ошибки возможно, если автоматизировать подготовку исходных данных о сетке элементов с помощью специальной программы.
Область, в которой ищется решение, предварительно разбивается на несколько фрагментов. Начало координат выбирается произвольно. Выбранная система координат называется глобальной. В каждом фрагменте в вершинах и на сторонах проставляются узловые точки. На плоскости X,Y задаются координаты узловых точек.
Каждый фрагмент отображается на квадрат с локальными координатами ,. Начало координат , выбирается в центре квадрата. Координаты и изменяются от -1 до 1. Такая система координат называется естественной.
В локальной системе координат фрагмент разбивается на прямоугольники. Полученные в локальной системе координат новые узловые точки отображаются обратно в глобальную систему координат по формулам
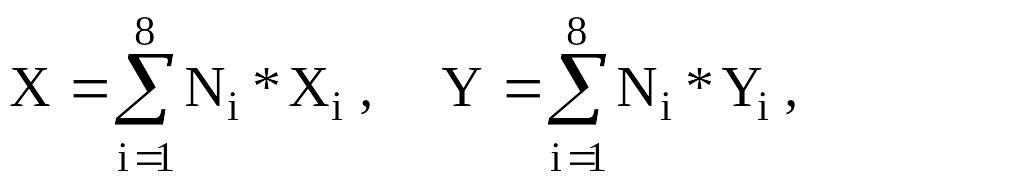 (1)
(1)
где Xi, Yi - глобальные координаты узлов фрагмента; Ni(,) - функции формы; X,Y - координаты новых узлов фрагмента, полученные после разбиения; 8 - начальное количество узлов фрагмента.
В качестве фрагментов используют четырехугольные элементы с восемью узлами. Функции Ni представляют собой полиномы второго порядка относительно локальных координат и . Поэтому отображение (1) будет квадратичным, а стороны элементов - параболы. Квадратичное отображение позволяет строить дискретную модель области с криволинейными границами.
Функции формы в выражении (1) для квадратичного отображения имеют вид
N1=-0.25(1-)(1-)(++1); N3= 0.25(1+)(1-)(--1); N5= 0.25(1+)(1+)(+-1); N7=-0.25(1-)(1+)(-+1); |
N2 = 0.5(1-2)(1-); N4 = 0.5(1-2)(1+); (2) N6 = 0.5(1-2)(1+); N8 = 0.5(1-2)(1-). |
Построение сетки с помощью квадратичного отображения для одного фрагмента показано на Рис.2.
1
5
6
7
8
7
6
4
1
2
3
5
Y
X
2
4
Y |
-1
<=
<= 1; -1 <=
<=
1
1
2
3
4
5
6
7
8
Сторона
4
Сторона 3
Сторона 1
Сторона 4
Сторона 2
X
8
6
1
4
7
5
3
2 |
Рис.2. Квадратичное отображение
На этом же рисунке показаны глобальные X,Y и локальные ,, координаты. Номера узлов в локальной системе координат изменяются от 1 до 8. Узлу 1 всегда соответствуют координаты ==-1. Остальные узлы нумеруются против часовой стрелки. В глобальной системе координат узлы нумеруются произвольно.
Равномерность разбиения фрагмента на элементы зависит от начального положения узлов 2,4,6,8 расположенных на стороне фрагмента. При сдвиге этих узлов от середины стороны сетка элементов будет неравномерной. Положение узлов на стороне фрагмента в локальной системе координат должно удовлетворять неравенствам
-1/2 < < 1/2, -1/2 < < 1/2. (3)
Дискретная модель области обычно конструируется из нескольких четырехугольных фрагментов, имеющих общие стороны. При переходе к новому фрагменту необходимо проверять каждую сторону на связность с другими фрагментами. Информация о соединении фрагментов задается матрицей связности. Количество строк в матрице равно числу фрагментов. Количество столбцов равно 4 (число сторон фрагмента). Если сторона не связана, то в строке матрицы связности, соответствующей номеру фрагмента и в колонке, соответствующей номеру стороны записывается 0. В противном случае записывается номер фрагмента, с которым граничит сторона. Порядок нумерации сторон фрагмента в локальной системе координат показан на Рис.1.1.б. Узлы на общей стороне фрагментов должны иметь одинаковые номера. Таким образом, для построения сетки элементов необходимо выполнить следующие действия:
1. Заданную область предварительно разбить на четырехугольные фрагменты с восемью узлами. Каждому фрагменту и узлу присваивается номер. Нумерация узлов и фрагментов выполняется произвольно. Выбирается глобальная система координат, в которой задаются X и Y координаты узлов.
2. В каждом фрагменте выбирается локальная система координат. Задается матрица связности фрагментов. Стороны фрагмента нумеруются в соответствии с Рис.1.1.б.
3. В каждом фрагменте задается количество разбиений по координатам и . Количество разбиений по называется числом строк, а по - числом столбцов. Для каждого фрагмента указываются глобальные номера узлов, заданные в пункте 1.
4. Фрагмент отображается на квадрат в локальной системе координат. В соответствии с заданным количеством строк и столбцов фрагмент разбивается на новые четырехугольники. По формулам (1) вычисляются координаты новых узлов в глобальной системе (обратное отображение). Полученные после разбиения узлы последовательно нумеруются, начиная от точки с координатами = -1, = +1 и двигаясь слева направо (при изменении от -1 до +1) и сверху вниз (при изменении от +1 до -1).
5. Номера граничных узлов сохраняются и используются при рассмотрении соседних фрагментов. Все узлы, пронумерованные ранее, пропускаются.



















