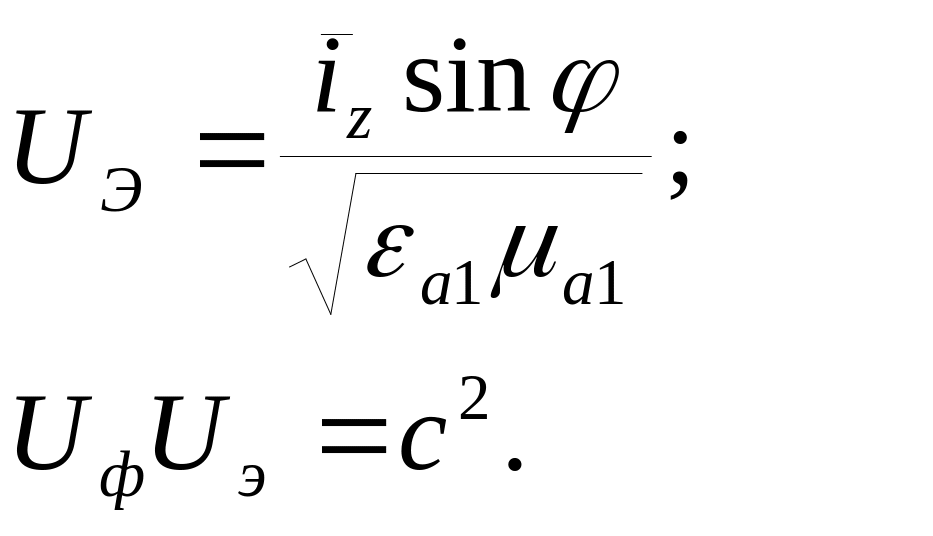- •Общие положения теории эмп Основные законы электродинамики
- •Материальные уравнения
- •Теорема Остроградского-Гаусса
- •Принцип перестановочной двойственности
- •Лемма Лоренца
- •Плоские электромагнитные волны
- •Частотная дисперсия характерна также для плазмы (ионизированный газ), для нее:
- •Поляризация волн
- •Частные случаи:
- •Граничные условия для векторов эмп
- •Нормальные составляющие
- •Тангесальные составляющие
- •Падение плоских электромагнитных волн на границу раздела двух сред
- •Нормальная поляризация.
- •Угол Брюстера
- •Угол полного внутреннего отражения
- •Рассмотрим более подробно второй закон Снелля
- •Рассмотрим поле во второй среде:
- •Отражение от системы слоёв
- •Частные случаи
- •Усвч (Устройства сверх – высоких частот)
- •Связь между продольными и поперечными составляющими электромагнитного поля
- •Будем полагать:
- •Прямоугольный металлический волновод
- •Структура эмп волны типа
- •Волна .
- •Щ ель эффективно излучает, если она перерезает линии поверхностного тока.
- •Круглый металлический волновод
- •Коаксиальный волновод
- •Высшие типы волн в коаксиальном волноводе.
- •Особенности использования коаксиального волновода
- •Полосковые линии передачи
- •С имметричная волновая линия.
- •В ысокодобротная линия.
- •Л иния с подвешенной подложкой.
- •Волноводы п и н формы
- •З амедляющие системы
- •Линия Губо
- •Диэлектрические волноводы
- •Потери в линиях передачи электромагнитной энергии
- •Коаксиальный волновод:
- •Прямоугольный и цилиндрический волноводы:
- •Распространение эмв в линиях конечной длины
- •Кпд линии
- •Возбуждение эм колебаний
- •Достаточно часто используют коаксиальные резонаторы, у которых кри значит: .
- •Магнитронный резонатор
- •Резонатор бегущей волны
- •Элементы свч трактов Волноводные тройники
- •Основные свойства волноводного тройника.
- •Элементы конструкций линий передачи свч
- •1.Неподвижные прямые соединения.
- •2. Подвижные соединения.
- •3.Вращающиеся сочленения.
- •Изгибы и скрутки линий передач свч
- •Емкость можно уменьшить, если уменьшить размер центрального проводника.
- •Трансформаторы типов
- •В клиновидном трансформаторе обычный прямоугольный волновод с помощью клиньев длиной (2в переходит в н образный волновод, имеющий пониженное волновое сопротивление.
- •Согласование линий передачи
- •Узкополосное согласование
- •Широкополосное согласование
- •Волноводно-ферритовые элементы
- •Случай продольной волны в поперечно намагниченном феррите
- •Рассмотрим работу циркуляторов, исследуемых в лабораторных работах
- •Развязывающие устройства
- •Н аправленные ответвители
- •Примеры использования циркулятора:
- •Фазирующие устройства
- •Механический фазовращатель «тромбонного типа».
- •Поляризационные устройства
- •Поляризационные устройства бывают механические и электрические.
- •Симметрирующие устройства (в дальнейшем су)
- •Конструкции симметрирующих устройств
- •Щелевые симметрирующие устройства
- •Симметрирующие устройства на основе плавных переходов
- •Коммутационные устройства свч на полупроводниковых диодах
- •Свч выключатели на коммутационных диодах
- •Полупроводниковые свч коммутаторы
- •Дискретные отражательные диодные фазовращатели свч
Угол Брюстера
В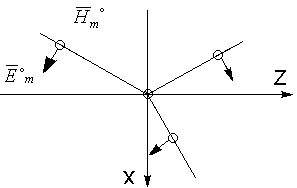 связи со сказанным, возникает вопрос о
том, какими свойствами должно обладать
вещество, чтобы являться ’’оптической
невидимкой’’.
связи со сказанным, возникает вопрос о
том, какими свойствами должно обладать
вещество, чтобы являться ’’оптической
невидимкой’’.
Так
как визуальное обнаружение любого тела
обусловлено волнами, отражёнными и
рассеянными телом под самыми различными
углами, то для этого необходимо, чтобы
R
и R
равнялись 0 для любого угла падения ,
что для реального диэлектрика означает![]() .
.
Т.е. электромагнитные свойства вещества неотличимы от свойств вакуума, если он – первая среда, или ( ): ZС2 = ZС1.
Если условие ZС = ZС не выполняется, то из условия следует:
для параллельной поляризации:
 ,
возводим в квадрат обе части равенства
и учтём второй закон Снеллиуса в
следующей форме:
,
возводим в квадрат обе части равенства
и учтём второй закон Снеллиуса в
следующей форме:
![]() .
.
Для
обычных диэлектриков![]() ,
после преобразований:
,
после преобразований:
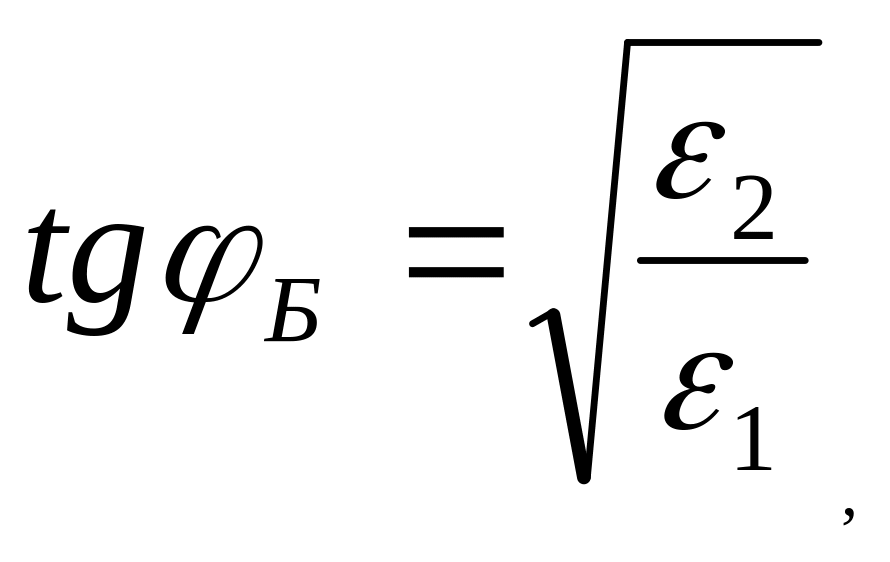
где
![]() –
–![]() угол
Брюстера
угол
Брюстера
Для обычных диэлектриков существует угол падения, при котором падающая волна целиком проходит во вторую среду.
В случае нормальной поляризации при
 ;
;
![]()
От границы раздела обычных диэлектриков волна с нормальной поляризацией отражается всегда.
Волна с эллиптической поляризацией отражается от границы всегда.
Угол полного внутреннего отражения
Отметим условия, при которых вещество полностью отражает падающие на него электромагнитные волны.
Например,
если
![]() при конечном ,
то коэффициенты отражения стремятся к
предельным значениям:
при конечном ,
то коэффициенты отражения стремятся к
предельным значениям:
R = - 1;
R = 1.
К этому предельному случаю очень близко подходят металлы, у них имеет большую мнимую часть. Металлы - почти идеальные зеркала для электромагнитных волн.
Если существуют вещества, у которых при конечной была бы весьма велика, то для них:
R=1;
R= -1.
R стремится к 1 для критической плазмы ( ).
Рассмотрим более подробно второй закон Снелля
Угол меняется от 0 до ( – предельное значение).
Угол падения, при котором , назовём критическим:
![]() ,
,
это
возможно, если
![]() .
.
При
> кр
правая часть
![]() становится больше единицы. Если
– вещественный, это невозможно.
становится больше единицы. Если
– вещественный, это невозможно.
Будем
полагать:
![]() .
.
Тогда:
![]() .
.
Чтобы
sin
достаточно:
![]() и
и
![]() ,
а cos
– мнимый.
,
а cos
– мнимый.
С учётом этого при любом :
![]()
То есть средняя плотность потока энергии одинакова в падающей и отражённой волнах.
Поле в первой среде (после того, как за скобки вынесли exp(i)):
![]() ;
;
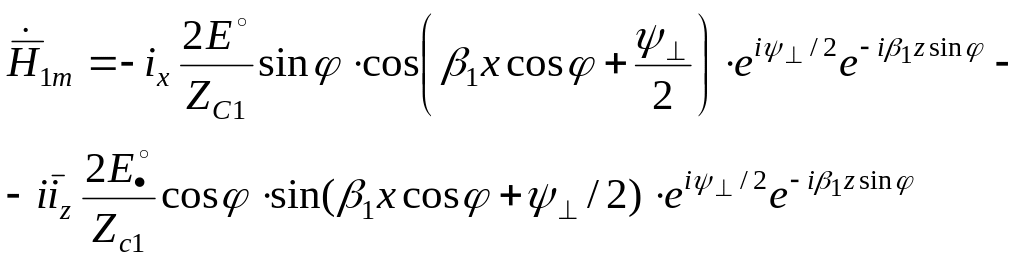
Итак, в первой среде ЭМП имеет структуру плоской волны, распространяющейся вдоль поверхности раздела (вдоль z) – направленная волна.
Поверхности равных фаз – плоскости, перпендикулярные Z.
Амплитуды E и H зависят от X и от .
Поверхности равных амплитуд–плоскости, перпендикулярные X.
Эта волна - неоднородная плоская волна, у которой есть продольная составляющая Hz.
(для волны с параллельной поляризацией–Ez).
Фазовая скорость:
![]() ,
,
то
есть
![]() больше
больше
![]() ,
но меньше
,
но меньше
![]() .
Причём, чем больше ,
тем меньше
.
.
Причём, чем больше ,
тем меньше
.
Длина
волны вдоль Z:
![]() .
.
Изменение
Е и Н вдоль оси Х имеет характер стоячей
волны в первой среде:
![]() .
.
Поперечные составляющие изменяются в фазе, а продольная сдвинута на 90, в результате комплексный вектор Пойнтинга:
![]()
Знак ’+’ – перпендикулярная поляризация.
Знак ‘_’ - параллельная поляризация.
В среднем энергия распространяется только вдоль оси Z, а в перпендикулярном по отношению к Z направлении – только реактивный поток энергии: