Тангесальные составляющие
Из произвольной точки на поверхности S раздела двух изотропных сред проведем единичную нормаль n0. Через нее проведем плоскость Р и на линии пересечения Р и S выделим малый отрезок l такой, чтобы считать его прямолинейным и неизменной в его пределах.
На отрезке l построим контур ABCD высотой h
-
касательная к
l,
-
нормаль к P,
образующий правовинтовую систему с
ABCD
и
.
Используем второе уравнение Максвелла:
,
где
.
Левую часть представим в виде суммы четырех интегралов:
и оставляя AB и CD в разных средах, устремляем h :
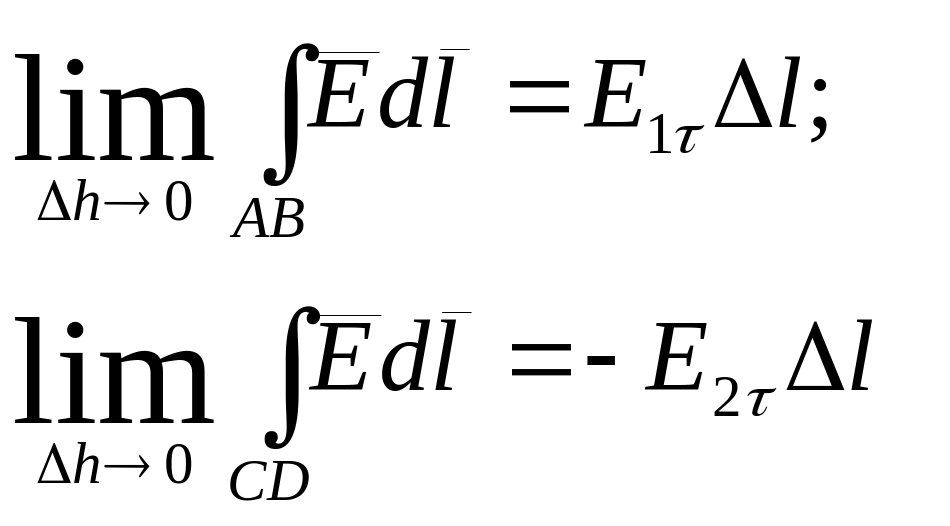
Так
как Е и
конечные величины, то:
.
А
,
то есть касательная, составляющая
вектора Е, непрерывна при переходе через
границу раздела двух сред.
Полная система граничных условий:
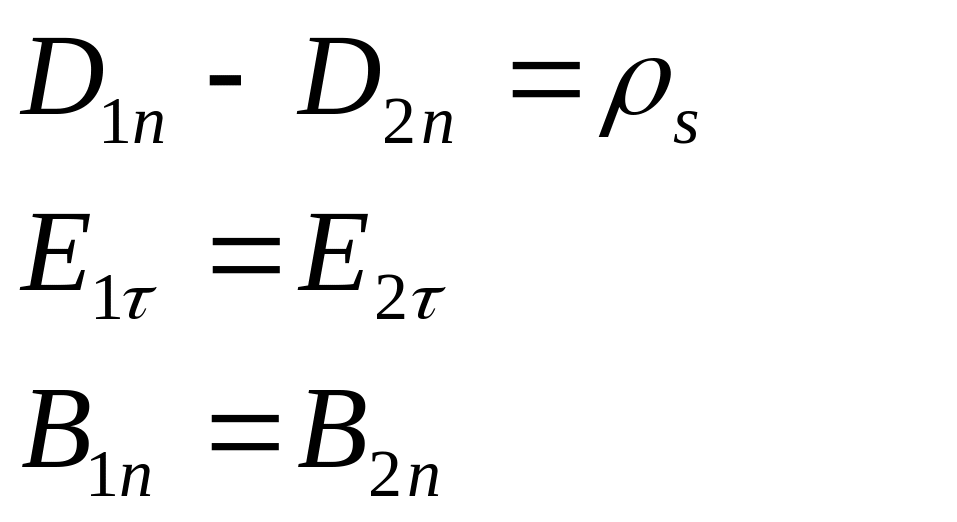
где
- плотность поверхностного тока,
направленного ортогонально вектору
(или его составляющая).
На
поверхности раздела с идеальным
проводником
,
внутри которого поле отсутствует,
согласно уравнению Максвелла будут
справедливы следующие граничные условия:
,
или для Н в векторной форме:
Падение плоских электромагнитных волн на границу раздела двух сред
Границу раздела будем полагать бесконечно протяженной. Плоскость, проходящая через нормаль к границе раздела параллельно направлению распространения, называют плоскостью падения.
Если вектор Е перпендикулярен этой плоскости, то волна – нормально поляризованная, если параллелен, волна – параллельно поляризованная.
Любую
другую ориентацию вектора Е следует
рассматривать как суперпозицию
.
Нормальная поляризация.
-
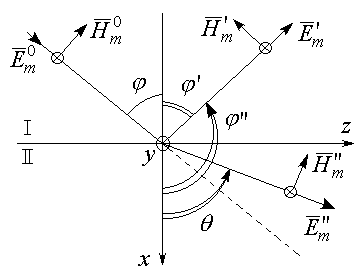угол падения.
В выбранной системе координат направляющие косинусы:
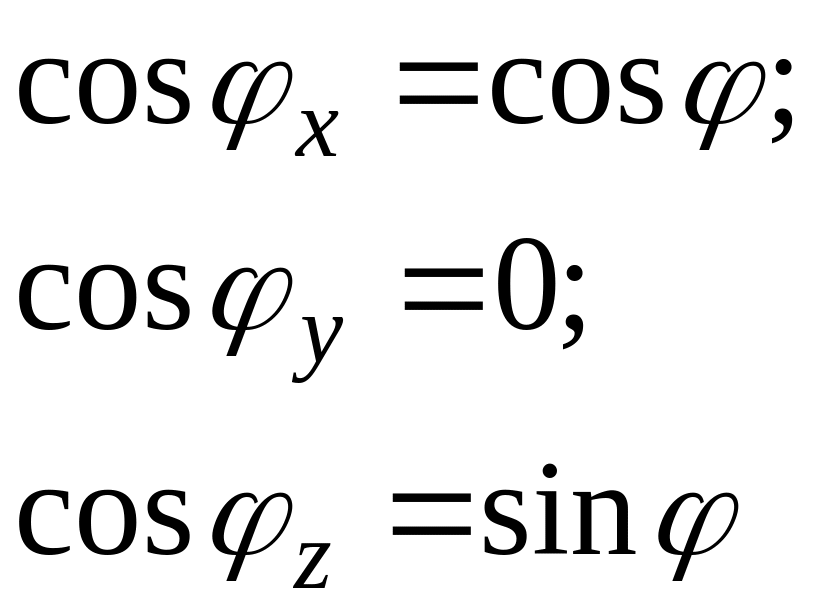и
Для амплитуд:
при условии 0Х
.
Граничные
условия:
.
Падающая
волна частично (или полностью) отражается
от границы и частично (или полностью)
проходит во вторую среду. Можно считать,
что ориентация векторов
относительно направления распространения
не меняется.
Для отраженной волны:
при
этом
и
.
Для преломленной волны:
при
.
Граничные условия должны выполняться при любых Z. Это возможно только, если зависимость от Z для всех трех векторов одинакова:
так как:
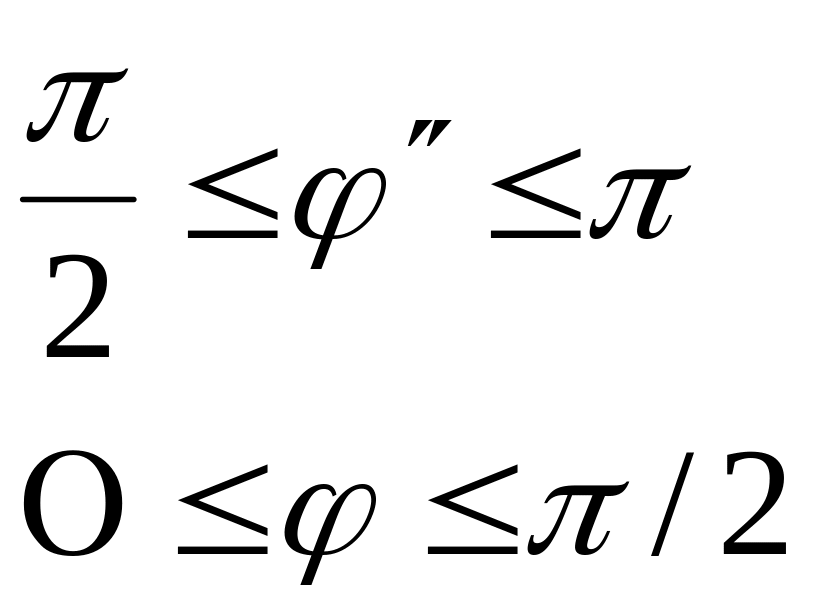
и угол падения равен углу отражения:
(2.23)
Из другого равенства:
(2.24)
n - показатель преломления среды:
Определим постоянные А и В на границе раздела (А и В амплитуды отражённой и преломлённой волн соответственно ):
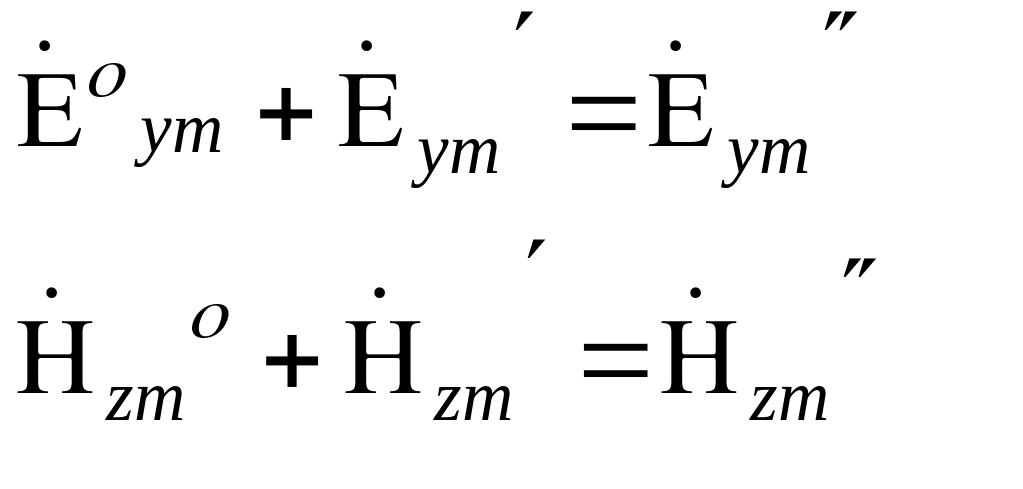
При Х = 0:
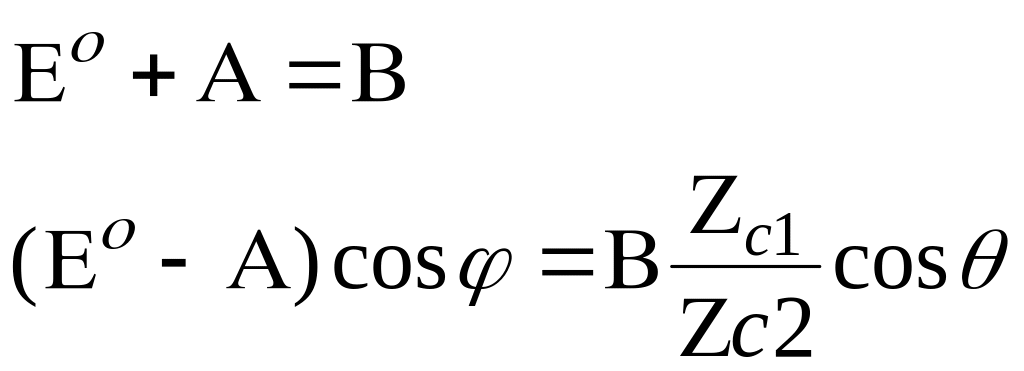
A и B пропорциональны E: А = RЕ, В = ТЕ.
R - коэффициент отражения, T - коэффициент преломления (коэффициенты Френеля).
В случае нормальной поляризации:
1+R=T;
1-R=
Т
Модуль R характеризует соотношение между амплитудами падающей и отражённой волны, а аргумент - сдвиг фаз между этими полями:
R
=
T
=
вывод при параллельной поляризации аналогичен - самостоятельно.
R
=
T
=
Остановимся на простейших следствиях, вытекающих из этих соотношений.
Для нормального падения ЭМВ имеем 0 и формулы для R и T переходят в:
R=
- R=
;
T=
T
=
.
При нормальном падении плоскость падения становится неопределённой и различие поляризаций пропадает.
Знак ’’минус’’ за счёт того, что R и T коэффициенты по электрическому полю, R и T - по магнитному.