Частотная дисперсия характерна также для плазмы (ионизированный газ), для нее:

;

;

.

где  - частота столкновений электронов с нейтральными молекулами,

_пл – собственная (плазменная) частота, при которой при  = 0, _а = 0.

,

где Ne – электронная концентрация.

Если потери отсутствуют, то фазовая скорость выражается:

Скорость переноса информации (скорость перемещения в пространстве энергии, или медленной огибающей, или группы волн):

Эта формула справедлива для узкополосных сигналов (можно применять для радиоимпульсов и т.д.).

Такая частотная зависимость приводит к расплыванию (увеличению длительности) импульсов.

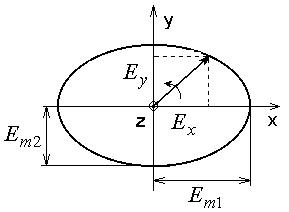
Поляризация волн

Полагаем, что вектор Е имеет две составляющие, и . Найдем положение кривой, которая служит геометрическим местом концов вектора Е суммарного процесса.

Перепишем:

,

возводим их в квадрат и складываем:

,

это уравнение эллипса, а про волну говорят, что это эллиптически поляризованная волна.

В этом случае вектор Е вращается против часовой стрелки, если смотреть с конца i_z – лево поляризованная волна.

Частные случаи:

1. Равна нулю одна из составляющих или сдвиг фаз между ними равен нулю. Тогда конец вектора Е перемещается вдоль линии произвольно, в общем случае, ориентированной относительно системы координат. Волна – линейно поляризованная.

2. Равны амплитуды Е_m1 = Е_m2, а сдвиг фаз - 90. Тогда кривая окружность, волну называют волной с круговой поляризацией.

Легко заметить, что суперпозиция двух волн с линейными поляризациями, сдвинутых по фазе и пространственно на 90, дают эллиптически поляризованную волну, две волны с круговыми поляризациями и противоположными направлениями вращения в результате суперпозиции дают волну линейно поляризованную.

Если рассматривать волну, распространяющуюся в направлении, не совпадающем с осью системы координат, то вместо пропорциональности

 exp(-iz)

следует записать

 exp(-iz').

Если выразить z через радиус вектор, проведенный из начала системы координат, конец которого лежит на волновом фронте, то z = .

Используем координаты Х,Y,Z:

Где , ,  - направляющие косинусы единичного вектора i_z:

.

В итоге  , где - волновой вектор: , а - волновое число.

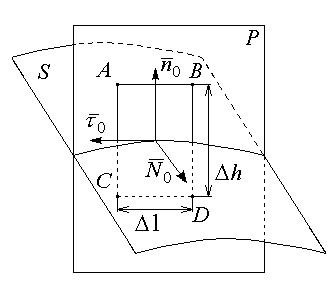
Граничные условия для векторов эмп

**для магнитного самостоятельно**

1. Нормальные составляющие

С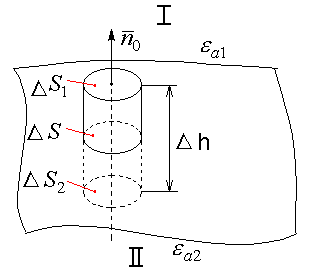 оотношения, показывающие связь между значениями векторов ЭМП в разных средах, у поверхности раздела называют граничными условиями. (Используют интегральную запись уравнений Максвелла). На поверхности раздела двух сред с параметрами соответственно, выделим малый элемент так чтобы:

1. его можно считать плоским;

2. распределение Dn в пределах должно быть равномерным.

Построим на цилиндр с основаниями в разных средах. Используем третье уравнение Максвелла:

.

Поверхность цилиндра:

.

Устремим так, чтобы оставались в разных средах:

;

Если заряд не сосредоточен на поверхности раздела, то:

и нормальная компонента вектора непрерывна при переходе из одной среды в другую. Если заряд распределен по поверхности раздела в виде бесконечно тонкого слоя с поверхностной плотностью:

тогда , то есть нормальная компонента вектора D претерпевает скачек на величину поверхностного заряда. Для вектора Е:

Нормальная компонента Е претерпевает разрыв. На самом деле поверхностных зарядов не бывает, толщина слоя конечна и D меняется постепенно. Но математическая модель удобнее.