Теорема Остроградского-Гаусса

Мы уже говорили, что токи и заряды являются источниками ЭМП, а также сами возникают под действием поля.

На практике приходится учитывать также токи и заряды, которые вызываются внешними источниками и практически не зависят от возбужденного ими ЭМП.

Такие токи принято называть "сторонними" и векторное поле плотности сторонних токов следует ввести, как заранее заданную функцию в уравнения Максвелла, а также в уравнение Умова-Пойнтинга:

,

где .

Сводка уравнений Максвелла:

* Уравнения в интегральной форме записать самостоятельно.

Это система дифференциальных уравнений в частных производных первого порядка относительно шести неизвестных функций (Е_Х Е_У Е_Z Н_Х Н_У Н_Z), которые зависят от трех пространственных координат и от времени t.

Так как в большинстве практических задач материальные среды можно считать линейными, то в них будет справедлив принцип суперпозиций ЭМП:

Если частные решения УМ, то решением будет и сумма вида: ( ).

Решение уравнений можно значительно упростить, если исключить временную переменную.

Любой сигнал может быть разложен на спектр гармонических составляющих по преобразованию Фурье.

Для гармонически изменяющего в некоторой заданной точке пространства вектора (например, E):

E_mx, Е_my, E_mz - амплитуды отдельных составляющих поля - соответствующие начальные фазы, по-другому это выражение можно записать:

Вектор принято называть комплексной амплитудой поля E в заданной точке пространства (считается, что частота поля  - известна).

пространственные, в общем случае, трехмерные векторы (изобразить вспомогательным вектором, вращающимся в комплексной плоскости нельзя).

Exp – эти множители характеризуют только фазы, т.е.

Не образуют угол 90⁰, а параллельны орту i_x и сдвинуты по фазе на 90⁰.

Связь между E(t) и :

Если подставить подобные выражения для всех векторов в уравнения Максвелла и сократить общий множитель, то получим:

Если объединить первое уравнение и пятое, то получим:

где

комплексная диэлектрическая проницаемость данного вещества, учитывающая и проводящая и поляризационные свойства.

Д ействительная часть - интенсивность процесса поляризации, мнимая - плотность токов проводимости (потери).

В комплексной плоскости

- угол диэлектрических потерь (в справочниках обычно приводят tg ) :

На частотах СВЧ диапазона для хороших диэлектриков tg =10^-510^-4, если tg >10^-3 - диэлектрик принято считать плохим.

Выразим через комплексные амплитуды вектор Пойнтинга.

Воспользуемся соотношениями:

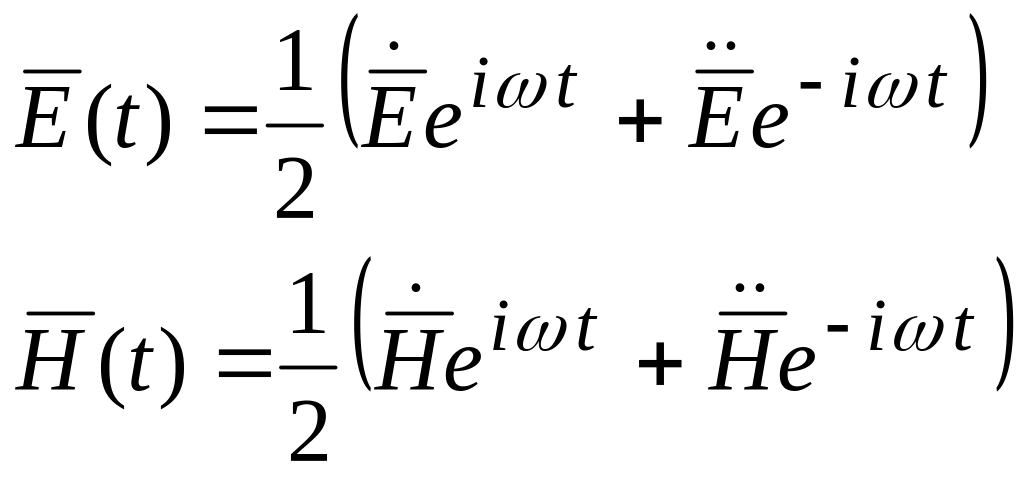
подставляем их в…

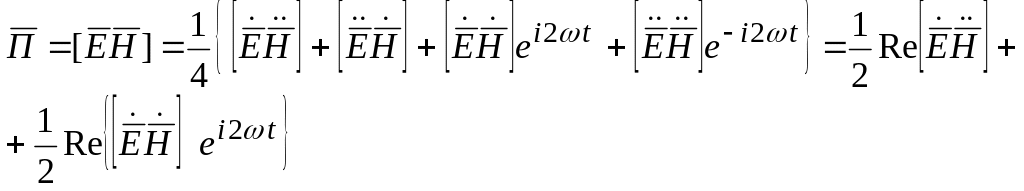
Первое слагаемое неизвестно во времени, а второе меняется с удвоенной частотой - колеблющаяся составляющая вектора Пойнтинга, среднее за период значение которой равно 0; .

Первое слагаемое практически равно плотности потока мощности усредненной за период (действительный вектор):

При анализе гармонических полей удобней использовать комплексный вектор Пойнтинга:

и

Комплексный вектор Пойнтинга аналогичен комплексной мощности гармонического колебания.

Если он чисто мнимый, то процесс не переносит мощности (перенос реактивной мощности).