7. Л иния с подвешенной подложкой.

а) низкие потери, малый разброс параметров, высокое Zв;

б) требует крепление, сравнительно большие габариты.

Часто в качестве подложек используют диэлектрик на основе оксида алюминия - поликор ( ), лейкосапфир ( ), кроме того, любые диэлектрики с низкими потерями ( 7..16 иногда до 10000-керамика).

Как видно из рисунков, ПЛ относится к направляющим системам открытого типа. Наличие нескольких изолированных проводников означает, что fкр=0, т.е. волна в ПЛ должна соответствовать волне Т-типа.

С трогий анализ достаточно сложный, но качественно структуру можно получить, деформируя коаксиальную линию:

Хотя полученная картина напоминает электростатическое поле в плоском конденсаторе, строгий анализ показывает, что из-за неоднородности по сечению диэлектрического заполнения ЭМП имеет все 6 составляющих, а следовательно зависит от частоты , т.е. дисперсия тем заметнее, чем больше . Но при условии, что a>>b; c>>b; c>>a; практически вся энергия сосредоточена внутри ПЛ и продольными составляющими можно пренебречь - такую волну называют волной - квази - Т типа.

Точно также (анализируя коаксиальную линию) можно получить картину волны первого высшего типа в ПЛ.

К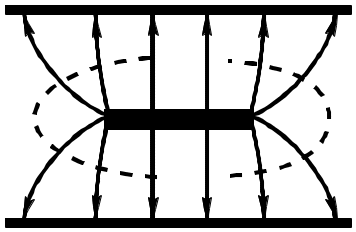 ак видно, на длине немного превышающей а, укладывается одна полуволна электрического поля ЭМВ, т.е. .

Волновое сопротивление в симметричной ПЛ:

,

где К(к) - полные эллиптические интегралы первого рода, , .

Для несимметричной ПЛ:

.

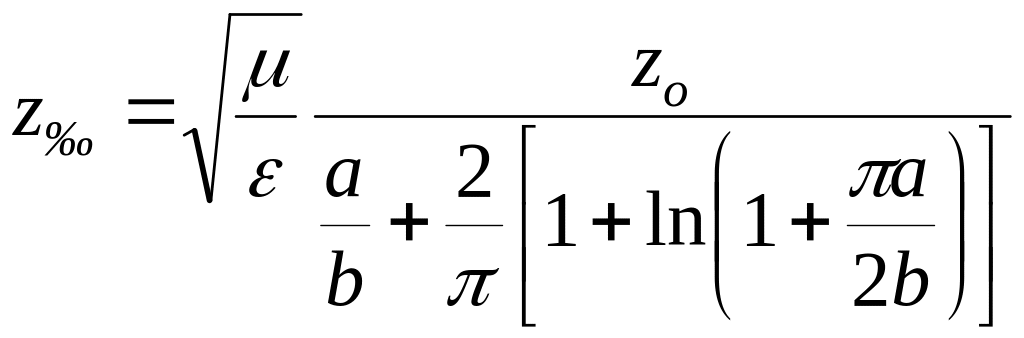О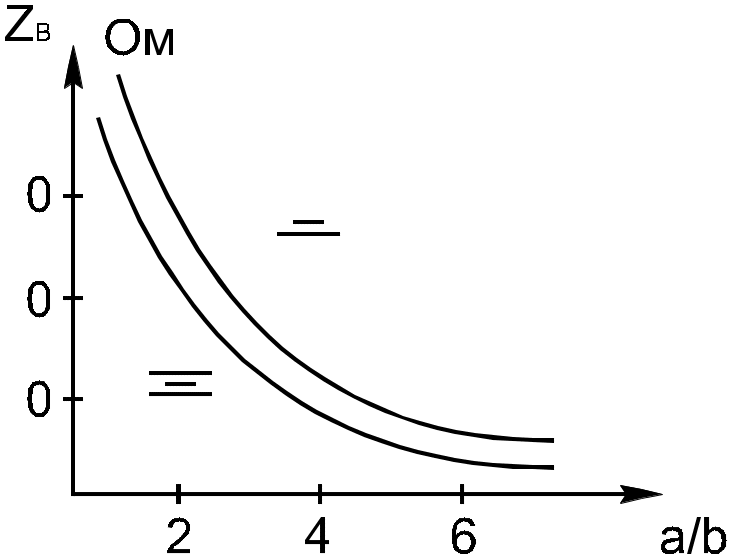 бе формулы получены в предположении, что толщина центрально проводника много меньше b.

Как показали эксперименты, по ПЛ можно передавать мощности того же порядка, что и в коаксиальной линии.

Для увеличения электрической прочности края центрального проводника закругляют.

Волноводы п и н формы

Э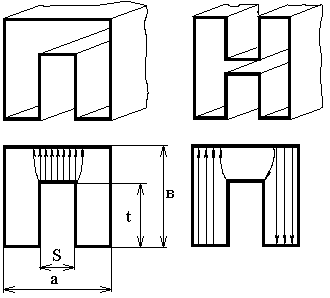 ти волноводы позволяют сохранять одномодовый режим в значительно более широкой полосе частот, а если так подобрать размеры, чтобы было близко к 2, то размеры таких волноводов будут значительно меньше.

Волны в этих волноводах условно называют , т.к. при эти структуры совпадут.

Для волны у волновода Н и П формы и прямоугольного волновода практически совпадают, т.к. ребро приходится на минимум Еy и не влияет на характер поля (почти):

Н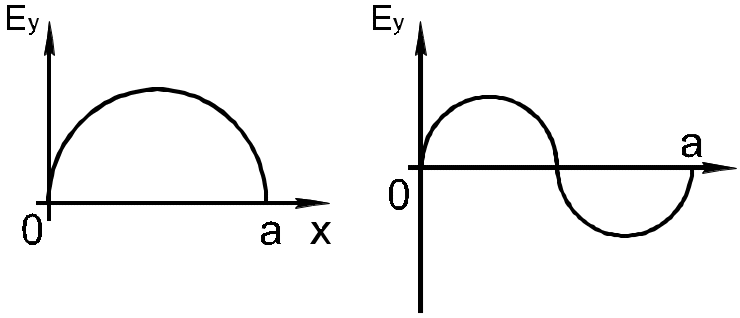 аличие ребра (в П-образном волноводе) для волны приводит к еще большей концентрации в центре. Структура в зазоре близка к волне Т-типа и при условии:

.

Причем, чем больше отношение t/b, тем больше .

Реально можно использовать при , обычно получают .

Недостатки:

1. Уменьшение электрической прочности.

2. Увеличение потерь.

Недостатки тем значительней, чем больше t.

З амедляющие системы

О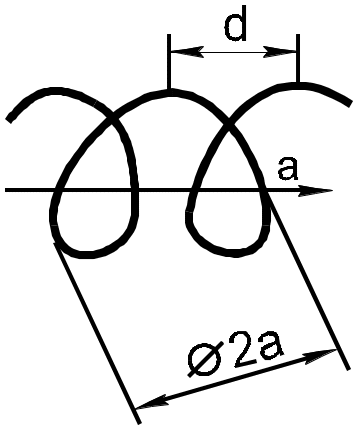 дна из первых практически используемых систем - спиральный волновод.

Замедление за счет того, что вдоль проводника бегущая волна тока распространяется со скоростью близкой к скорости света, но проекция на ось дает скорость ниже скорости света.

Коэффициент замедления, как видно из рисунка:

(3.24)

- угол намотки спирали, АВ - путь вдоль провода, АС- расстояние по оси волновода.

Из этого выражения следует, что не зависит от частоты (нет дисперсии).

Формула (3.24) справедлива, если , иначе волна «перескакивает» с витка на виток.

Строгая теория - много сложнее.

Д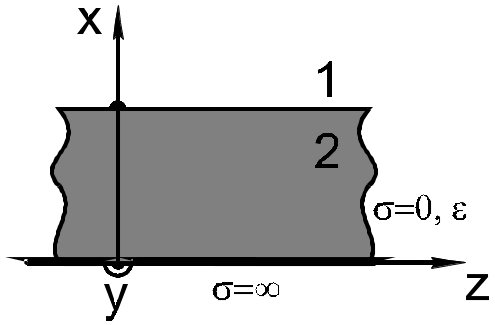 иэлектрическая замедляющая система.

1 - вакуум.

2 - немагнитный диэлектрик.

Сделаем предположения:

1. Длина волны в волноводе .

2. Система бесконечно протяженна вдоль *y и z.

3. Исследуется гармоническая волна, распространяющаяся вдоль z.

Вектор Н - имеет одну составляющую неизменную вдоль y: , силовые линии - бесконечные нити параллельные оси y.

Исследуем поле в вакууме: , решение ищем в виде: ,

тогда: , , где р - аналог поперечного волнового числа в полых волноводах.

Общее решение: .

Поле не может бесконечно возрастать, т.е. В=0 и .

Замедленная волна является поверхностной, амплитуда убывает по экспоненте при удалении от границы раздела.

Чем меньше (меньше ), тем больше р и поле сильнее «прижимается» к направляющей системе.

Составляющие Е найдем из первого уравнения Максвелла: .

Вычисляем ротор в декартовой системе координат:

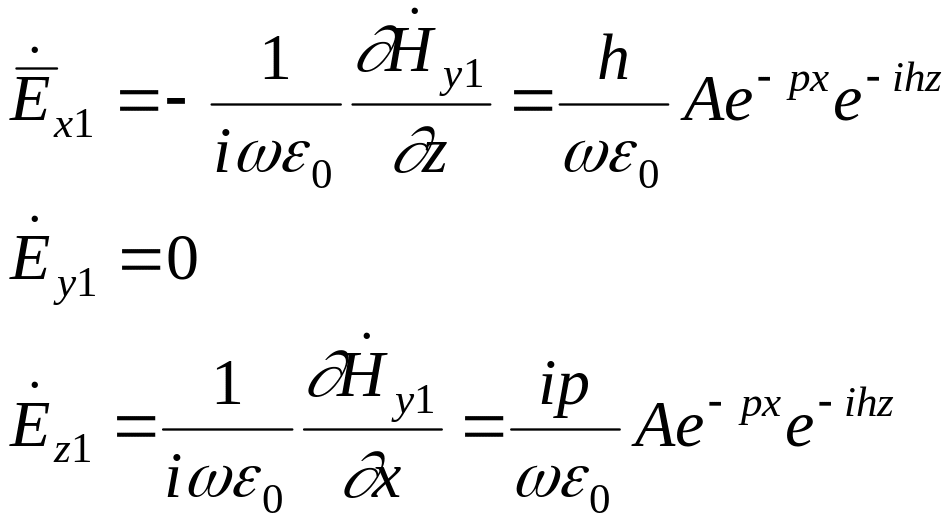
Полученная волна – Е – типа, у которой Пz - чисто действительная, Пx - мнимая.

Поле во 2-й среде , решение в виде: , причем h - одно и то же в 1-й и 2-й среде (единый волновой процесс).

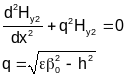
Общее решение: .

С и D следует выбирать граничных условий при x = a, x = 0.

На поверхности идеального проводника: должна обращаться в ноль, то есть: D=0 и .

Остальные составляющие:

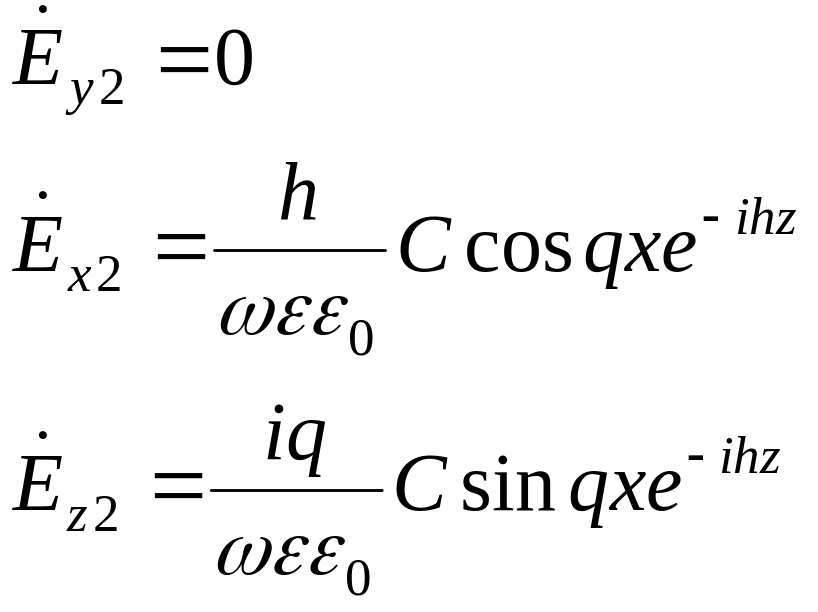
Используем граничные условия на границе раздела вакуум - диэлектрик при х=а .

Подставляем выражения:

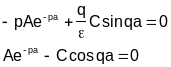
Чтобы система имела отличные от нуля решения, ее определитель должен обращаться в ноль, т.е.:

,

или в безразмерном виде: (3.25)

Уравнение (3.25) - дисперсионное уравнение замедляющей системы.

Чтобы определить q и p следует использовать: (3.26)

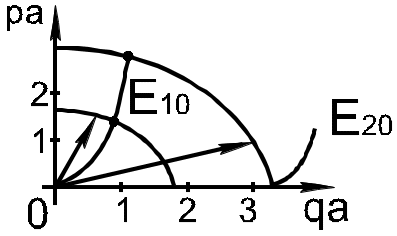
Уравнение (3.26) описывает окружности радиуса: .

Пересечение кривых - решение; первый индекс - номер корня, второй - поле однородно по y.

- низший тип волны существующей при любой частоте и толщине слоя диэлектрика:

.

Одноволновой режим вплоть до значения (для волн Е-типа), т.е.: .

С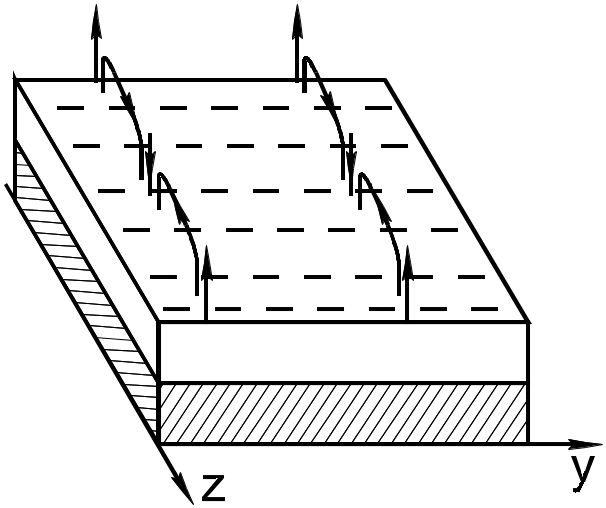 труктура для :

Отношение касательных к границе раздела - составляющих Е и Н называют поверхностным сопротивлением:

.

Величина - чисто мнимая (реактивное, индуктивное по характеру сопротивление), т.е. отсутствует средний за период поток энергии вдоль оси х.

Вывод для вол Н-типа аналогичен и для них , и для самой низшей волны , т.е. реальный одномодовый диапазон для всех типов волн .

Следует отметить, что в качестве линий замедленных волн можно использовать любые системы с реактивным поверхностным сопротивлением.

С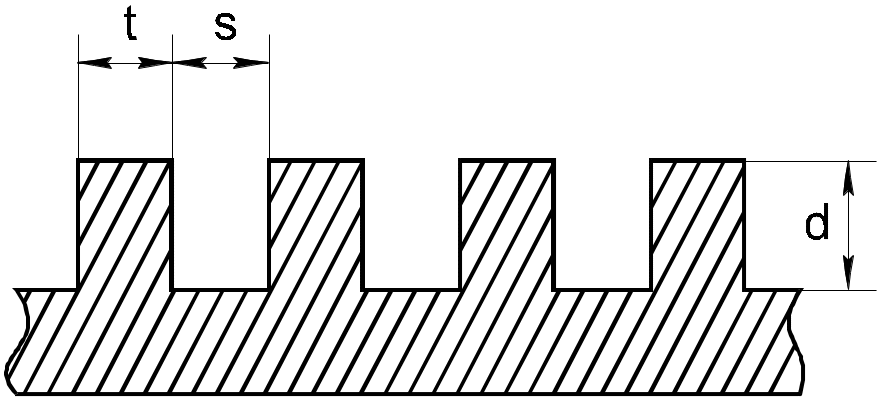 уществует много способов создания реактивного поверхностного сопротивления, например:

Каждая канавка подобна отрезку линии длиной d.

Если , то сопротивление чисто мнимое и имеет характер L. Если (S+t) , то можно пренебречь влиянием тонких перегородок и полагать, что вблизи поверхности имеется плоскость с реактивным сопротивлением.

Структура почти такая же, как у диэлектрика с металлом и .

Такие замедляющие системы обычно используют как элемент антенных систем:

.

Свернутая в трубочку - антенна на луноходе, обратная - диафрагмированный волновод.